2016 AMC 12B Problems/Problem 21
Contents
[hide]Problem
Let ![]() be a unit square. Let
be a unit square. Let ![]() be the midpoint of
be the midpoint of ![]() . For
. For ![]() let
let ![]() be the intersection of
be the intersection of ![]() and
and ![]() , and let
, and let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() . What is
. What is
![]()
![]()
Solutions
Solution 1
We start with ![]() for
for ![]()
![]() and
and ![]() so we have
so we have ![]() Repeating this same process for subsequent
Repeating this same process for subsequent ![]() s yields
s yields ![]() We can generalize this by saying
We can generalize this by saying ![]() Then
Then ![]() Let
Let ![]() and let
and let ![]()
![]() and
and ![]() are similar with side length ratio
are similar with side length ratio ![]() , so
, so ![]() Now, we can express the area of
Now, we can express the area of ![]() (which is
(which is ![]() since it's just half the square) as
since it's just half the square) as ![]() and we can express the area of
and we can express the area of ![]() as
as ![]() We have a system of equations:
We have a system of equations:
![]()
![]()
Solving, we get ![]() So now the problem becomes
So now the problem becomes  . We can rewrite this as
. We can rewrite this as
![]()
All terms cancel except for the ![]() on the inside and
on the inside and ![]() on the outside, so the answer is
on the outside, so the answer is ![]()
Solution 2
(By Qwertazertl)
We are tasked with finding the sum of the areas of every ![]() where
where ![]() is a positive integer. We can start by finding the area of the first triangle,
is a positive integer. We can start by finding the area of the first triangle, ![]() . This is equal to
. This is equal to ![]() ⋅
⋅ ![]() ⋅
⋅ ![]() . Notice that since triangle
. Notice that since triangle ![]() is similar to triangle
is similar to triangle ![]() in a 1 : 2 ratio,
in a 1 : 2 ratio, ![]() must equal
must equal ![]() (since we are dealing with a unit square whose side lengths are 1).
(since we are dealing with a unit square whose side lengths are 1). ![]() is of course equal to
is of course equal to ![]() as it is the mid-point of CD. Thus, the area of the first triangle is
as it is the mid-point of CD. Thus, the area of the first triangle is ![]() ⋅
⋅ ![]() ⋅
⋅ ![]() .
.
The second triangle has a base ![]() equal to that of
equal to that of ![]() (see that
(see that ![]() ~
~ ![]() ) and using the same similar triangle logic as with the first triangle, we find the area to be
) and using the same similar triangle logic as with the first triangle, we find the area to be ![]() ⋅
⋅ ![]() ⋅
⋅ ![]() . If we continue and test the next few triangles, we will find that the sum of all
. If we continue and test the next few triangles, we will find that the sum of all ![]() is equal to
is equal to
![]() or
or
![]()
This is known as a telescoping series because we can see that every term after the first ![]() is going to cancel out. Thus, the summation is equal to
is going to cancel out. Thus, the summation is equal to ![]() and after multiplying by the half out in front, we find that the answer is
and after multiplying by the half out in front, we find that the answer is ![]() .
.
Solution 3
(By mastermind.hk16)
Note that ![]() . So
. So ![]()
Hence ![]()
We compute ![]() because
because ![]() as
as ![]() .
.
Solution 4
(By user0003)
We plot the figure on a coordinate plane with ![]() and
and ![]() in the positive y-direction from the origin. If
in the positive y-direction from the origin. If ![]() for some
for some ![]() , then the line
, then the line ![]() can be represented as
can be represented as ![]() . The intersection of this and
. The intersection of this and ![]() , which is the line
, which is the line ![]() , is
, is
![]() .
.
As ![]() is the projection of
is the projection of ![]() onto the x-axis, it lies at
onto the x-axis, it lies at ![]() . We have thus established that moving from
. We have thus established that moving from ![]() to
to ![]() is equivalent to the transformation
is equivalent to the transformation ![]() on the x-coordinate. The closed form of of the x-coordinate of
on the x-coordinate. The closed form of of the x-coordinate of ![]() can be deduced to be
can be deduced to be ![]() , which can be determined empirically and proven via induction on the initial case
, which can be determined empirically and proven via induction on the initial case ![]() . Now
. Now
![]()
suggesting that ![]() is equivalent to
is equivalent to ![]() . The sum of this from
. The sum of this from ![]() to
to ![]() is a classic telescoping sequence as in Solution 1 and is equal to
is a classic telescoping sequence as in Solution 1 and is equal to ![]() .
.
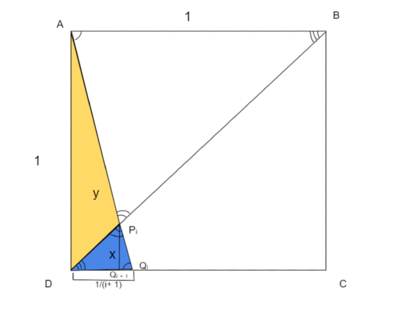
Solution 5 Diagram and Detailed Steps
Midpoint ![]() of
of ![]() :
: ![]()
Equation of ![]() : Slope
: Slope ![]() Equation:
Equation: ![]()
Line ![]() : - Equation:
: - Equation: ![]()
Intersection ![]() of
of ![]() and
and ![]() :
:
- Solve:Therefore,

Now, using the pattern for subsequent points ![]() and
and ![]() :
:
General ![]() - For
- For ![]() ,
, ![]()
Equation of ![]() Slope
Slope ![]() Equation:
Equation: ![]()
Intersection ![]() of
of ![]() and
and ![]() :
:
- Line:
Solve:
- Therefore,

![]() is the foot of the perpendicular from
is the foot of the perpendicular from ![]() to
to ![]() , so
, so ![]()
Area of ![]() =
= ![]()
This recursive process confirms the telescoping series:
![]()
Most terms cancel, and we are left with: ![]() .
.
Video Solution by CanadaMath (Problem 21-25)
https://www.youtube.com/watch?v=P3jJDLGyF2w&t=1546s
~THEMATHCANADIAN
See Also
| 2016 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 20 |
Followed by Problem 22 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()