Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2020 AMC 12A Problems/Problem 12

Problem

Line $l$ in the coordinate plane has equation $3x-5y+40=0$. This line is rotated $45^{\circ}$ counterclockwise about the point $(20,20)$ to obtain line $k$. What is the $x$-coordinate of the $x$-intercept of line $k?$

$\textbf{(A) } 10 \qquad \textbf{(B) } 15 \qquad \textbf{(C) } 20 \qquad \textbf{(D) } 25 \qquad \textbf{(E) } 30$

Solution 1

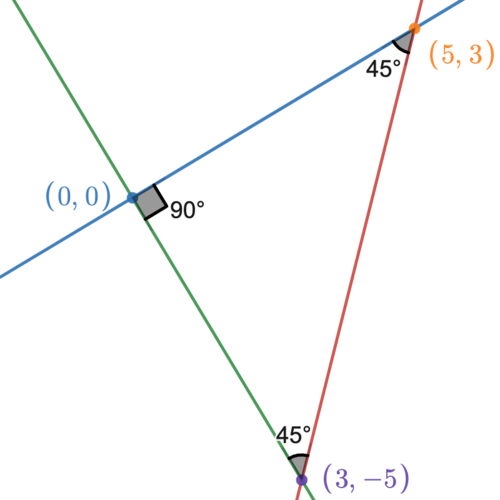
AMC 12A 2020 Question-12 Solution-1.png

The slope of the line is $\frac{3}{5}$. We must transform it by $45^{\circ}$.

$45^{\circ}$ creates an isosceles right triangle, since the sum of the angles of the triangle must be $180^{\circ}$ and one angle is $90^{\circ}$. This means the last leg angle must also be $45^{\circ}$.

In the isosceles right triangle, the two legs are congruent. We can therefore construct an isosceles right triangle with a line of $\frac{3}{5}$ slope on graph paper. That line with $\frac{3}{5}$ slope starts at $(0,0)$ and will go to $(5,3)$, the vector $<5, 3 >$.

Construct another line from $(0,0)$ to $(3,-5)$, the vector $<3,-5>$. This is $\perp$ and equal to the original line segment. The difference between the two vectors is $<2,8>$, which is the slope $4$, and that is the slope of line $k$.

Furthermore, the equation $3x-5y+40=0$ passes straight through $(20,20)$ since $3(20)-5(20)+40=60-100+40=0$, which means that any rotations about $(20,20)$ would contain $(20,20)$. We can create a line of slope $4$ through $(20,20)$. The $x$-intercept is therefore $20-\frac{20}{4} = \boxed{\textbf{(B) } 15.}$ ~lopkiloinm ~ShawnX (diagram)

Solution 2

Since the slope of the line is $\frac{3}{5}$, and the angle we are rotating around is x, then $\tan x = \frac{3}{5}$ $\tan(x+45^{\circ}) = \frac{\tan x + \tan(45^{\circ})}{1-\tan x*\tan(45^{\circ})} = \frac{0.6+1}{1-0.6} = \frac{1.6}{0.4} = 4$

Hence, the slope of the rotated line is $4$. Since we know the line intersects the point $(20,20)$, then we know the line is $y=4x-60$. Set $y=0$ to find the x-intercept, and so $x=\boxed{15}$

~Solution by IronicNinja

Solution 3

[asy] draw((0,0)--(20, 0)--(20, 20)--(0, 20)--cycle); draw((20, 20)--(0, 8)); draw((15, 0)--(20, 20)); dot("$P$", (20, 20)); dot("$A$", (0, 8), dir(75)); dot("$B$", (15, 0), dir(45)); dot("$X$", (20, 0)); dot("$Y$", (0, 20), dir(50)); [/asy]

Let $P$ be $(20, 20)$ and $X, Y$ be $(20, 0)$ and $(0, 20)$ respectively. Since the slope of the line is $3/5$ we know that $\tan{\angle{YPA}} = 3/5.$ Segments $\overline{PA}$ and $\overline{PB}$ represent the before and after of rotating $l$ by 45 counterclockwise. Thus, $\angle{XPB} = 45 - \angle{YPA}$ and \[BX = 20 \tan{\angle{XPB}} = 20 \cdot \frac{1 - 3/5}{1 + 3/5} = 5\] by tangent addition formula. Since $BX$ is 5 and the sidelength of the square is 20 the answer is $20 - 5 \implies \boxed{\textbf{B}}.$

Solution 4 (Cheap)

Using the protractor you brought, carefully graph the equation and rotate the given line $45^{\circ}$ counter-clockwise about the point $(20,20)$. Scaling everything down by a factor of 5 makes this process easier.

It should then become fairly obvious that the x intercept is $x=\boxed{15}$ (only use this as a last resort).

~Silverdragon

Solution 5 (Rotation Matrix)

First note that the given line goes through $(20,20)$ with a slope of $\frac{3}{5}$. This means that $(25,23)$ is on the line. Now consider translating the graph so that $(20,20)$ goes to the origin, then $(25,23)$ becomes $(5,3)$. We now rotate the line $45^\circ$ about the origin using a rotation matrix. This maps $(5,3)$ to \[\begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}\begin{bmatrix} 5 \\ 3\end{bmatrix}=\begin{bmatrix}\sqrt{2} \\ 4\sqrt{2}\end{bmatrix}\] The line through the origin and $(\sqrt{2}, 4\sqrt{2})$ has slope $4$. Translating this line so that the origin is mapped to $(20,20)$, we find that the equation for the new line is $4x-60$, meaning that the $x$-intercept is $x=\frac{60}{4}=\boxed{\textbf{(B) }15}$.

Solution 6 (Angle Bisector)

Note $(20,20)$ is on the line. Construct the perpendicular line $5x+3y-160=0$. This creates a right triangle that intersects the x-axis at $(\frac{-40}{3},0)$ and $(32,0)$ a distance of $136/3$ apart. The $45^\circ$ transformation will bisect the right angle. The angle bisector theorem tells us the $136$ will split in ratio to the lengths of the sides. These are $\sqrt{12^2+20^2}$ and $\sqrt{\frac{100}{3}^2 + 20^2} = 4\sqrt{34}$ and $\frac{20}{3}\sqrt{34}$. Thus the x intercept will split the line from $\frac{-40}{3}$ to $32$ into a ratio of $5:3$ making the x-intercept $15$.

Solution 7 (Complex Numbers)

Converting to the complex plane, we can see that two numbers on the line are $8i$ and $5+11i$. Translating $20+20i$ to the origin, we get $8i-20-20i = -20-12i$ and $5+11i-20-20i = -15-9i$. Multiplying each of them by $e^{\pi i/4}$, we get $-4\sqrt 2 - 16 \sqrt2 i$ and $-3\sqrt 2 - 12 \sqrt 2 i$. This line has a slope of $4$. Now, back to the cartesian plane. We have a line passing through $(20, 20)$ with slope $4$ which gives the equation as $y = 4x-60$ which implies the $x$ coordinate of the $x$ intercept is $60/4 = 15$.

~rocketsri (minor error corrected by kn07)

Solution 8 (quick)

A quick check tells us that $(20,20)$ falls on the given line. Common sense tells us that if the slope of the original line is $1$, or 45 degrees from the horizontal, a 45 counter clockwise rotation will result in a vertical line, and the x-intercept will be $(20,0)$. Thinking of a 45 degree counter clockwise rotation as a 90 degree counter clockwise rotation that is bisected will helps in visualizing this line of reasoning. Therefore, it follows that if the original line is made steeper, then the x-intercept will move away from $(20,0)$ to the right. If the original line is made lower, then the opposite will happen. Our given line has slope $3/5$, so the answer must be $A$ or $B$. $A$ can be eliminated because an x-intercept of $(10,0)$ can only occur when the original line is horizontal. In conclusion, the answer must be $\boxed{\textbf{(B) }15}$.

~jackshi2006

See Also

2020 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_AMC_12A_Problems/Problem_12&oldid=200920"