2020 AMC 12A Problems/Problem 17
Contents
[hide]Problem
The vertices of a quadrilateral lie on the graph of ![]() , and the
, and the ![]() -coordinates of these vertices are consecutive positive integers. The area of the quadrilateral is
-coordinates of these vertices are consecutive positive integers. The area of the quadrilateral is ![]() . What is the
. What is the ![]() -coordinate of the leftmost vertex?
-coordinate of the leftmost vertex?
![]()
Solution 1
Let the coordinates of the quadrilateral be ![]() . We have by shoelace's theorem, that the area is
. We have by shoelace's theorem, that the area is
 We know that the numerator must have a factor of
We know that the numerator must have a factor of ![]() , so given the answer choices,
, so given the answer choices, ![]() is either
is either ![]() or
or ![]() . If
. If ![]() , the expression
, the expression ![]() does not evaluate to
does not evaluate to ![]() , but if
, but if ![]() , the expression evaluates to
, the expression evaluates to ![]() . Hence, our answer is
. Hence, our answer is ![]() .
.
Solution 2
Like above, use the shoelace formula to find that the area of the quadrilateral is equal to ![]() . Because the final area we are looking for is
. Because the final area we are looking for is ![]() , the numerator factors into
, the numerator factors into ![]() and
and ![]() , which one of
, which one of ![]() and
and ![]() has to be a multiple of
has to be a multiple of ![]() and the other has to be a multiple of
and the other has to be a multiple of ![]() . Clearly, the only choice for that is
. Clearly, the only choice for that is ![]()
~Solution by IronicNinja
Solution 3
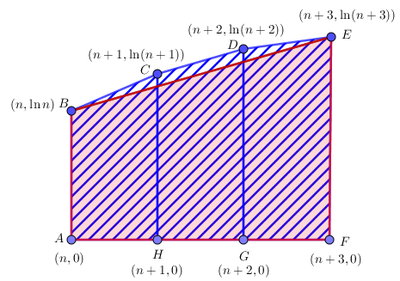
How ![]() is a concave function, then:
is a concave function, then:
Therefore ![]() , all quadrilaterals of side right are trapezius
, all quadrilaterals of side right are trapezius
![]()
![]()
![]()
![]()
~Solution by AsdrúbalBeltrán
Video Solution by TheBeautyofMath
https://www.youtube.com/watch?v=Eq2A2TTahqU?t=583 Another example of shoelace theorem included earlier in the video
~IceMatrix
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 16 |
Followed by Problem 18 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()