2020 AMC 12B Problems/Problem 12
Contents
[hide]- 1 Problem
- 2 Diagram
- 3 Solution 1 (Pythagorean Theorem)
- 4 Solution 2 (Power of a Point)
- 5 Solution 3 (Law of Cosines)
- 6 Solution 4 (Reflections)
- 7 Solution 5 (Basically Solution 2 With Motivation)
- 8 Solution 6 (Double Power of a Point)
- 9 Solution 7 (Cheating)
- 10 Solution 7 (Coordinate Geometry + Vieta)
- 11 Video Solution by OmegaLearn
- 12 Video Solution by On The Spot STEM
- 13 Video Solution by TheBeautyOfMath
- 14 See Also
Problem
Let ![]() be a diameter in a circle of radius
be a diameter in a circle of radius ![]() Let
Let ![]() be a chord in the circle that intersects
be a chord in the circle that intersects ![]() at a point
at a point ![]() such that
such that ![]() and
and ![]() What is
What is ![]()
![]()
Diagram
![[asy] /* Made by Shihan; edited by MRENTHUSIASM */ size(250); pair O, A, B, C, D, E; O = origin; A = (-5*sqrt(2),0); B = (5*sqrt(2),0); E = (5*sqrt(2)-2*sqrt(5),0); path p; p = Circle(O,5*sqrt(2)); C = intersectionpoint(p,E--E+10*dir(135)); D = intersectionpoint(p,E--E+10*dir(-45)); draw(p); dot(O,linewidth(4)); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$E$",E,1.5*dir(135/2),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); draw(A--B^^C--D); label("$45^\circ$",E,3.5*dir(155.5),red+fontsize(10)); label("$5\sqrt2$",midpoint(A--O),S); label("$2\sqrt5$",midpoint(E--B),S); [/asy]](http://latex.artofproblemsolving.com/7/3/0/73095518b62a21f7ac5840b39abebb5bec9386ec.png) ~Shihan ~MRENTHUSIASM
~Shihan ~MRENTHUSIASM
Solution 1 (Pythagorean Theorem)
Let ![]() be the center of the circle, and
be the center of the circle, and ![]() be the midpoint of
be the midpoint of ![]() . Let
. Let ![]() and
and ![]() . This implies that
. This implies that ![]() . Since
. Since ![]() , we now want to find
, we now want to find ![]() . Since
. Since ![]() is a right angle, by Pythagorean theorem
is a right angle, by Pythagorean theorem ![]() . Thus, our answer is
. Thus, our answer is ![]() .
.
~JHawk0224
Solution 2 (Power of a Point)
Let ![]() be the center of the circle, and
be the center of the circle, and ![]() be the midpoint of
be the midpoint of ![]() . Draw triangle
. Draw triangle ![]() , and median
, and median ![]() . Because
. Because ![]() ,
, ![]() is isosceles, so
is isosceles, so ![]() is also an altitude of
is also an altitude of ![]() .
. ![]() , and because angle
, and because angle ![]() is
is ![]() degrees and triangle
degrees and triangle ![]() is right,
is right, ![]() . Because triangle
. Because triangle ![]() is right,
is right, ![]() . Thus,
. Thus, ![]() .
.
We are looking for ![]() +
+ ![]() which is also
which is also ![]() .
.
Because ![]() ,
, ![]() .
.
By Power of a Point, ![]() , so
, so ![]() .
.
Finally, ![]() .
.
Solution 3 (Law of Cosines)
Let ![]() be the center of the circle. Notice how
be the center of the circle. Notice how ![]() , where
, where ![]() is the radius of the circle. By applying the law of cosines on triangle
is the radius of the circle. By applying the law of cosines on triangle ![]() ,
, ![]()
Similarly, by applying the law of cosines on triangle ![]() ,
, ![]()
By subtracting these two equations, we get ![]() We can rearrange it to get
We can rearrange it to get ![]()
Because both ![]() and
and ![]() are both positive, we can safely divide both sides by
are both positive, we can safely divide both sides by ![]() to obtain
to obtain ![]() . Because
. Because ![]() ,
, ![]()
Through power of a point, we can find out that ![]() , so
, so ![]()
~Math_Wiz_3.14 (legibility changes by eagleye)
Solution 4 (Reflections)
![[asy] /* Made by sofas103; edited by MRENTHUSIASM */ size(250); pair O, A, B, C, D, E, D1; O = origin; A = (-5*sqrt(2),0); B = (5*sqrt(2),0); E = (5*sqrt(2)-2*sqrt(5),0); path p; p = Circle(O,5*sqrt(2)); C = intersectionpoint(p,E--E+10*dir(135)); D = intersectionpoint(p,E--E+10*dir(-45)); D1 = (D.x,-D.y); draw(p); dot("$O$",O,1.5*S,linewidth(4)); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$E$",E,1.5*dir(180+135/2),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); dot("$D'$",D1,1.5*dir(D1),linewidth(4)); draw(A--B^^C--D^^C--D1--O--cycle^^D1--E); [/asy]](http://latex.artofproblemsolving.com/6/a/d/6adcf26313c5d271d38c4c010cc3516799a2139a.png) Let
Let ![]() be the center of the circle. By reflecting
be the center of the circle. By reflecting ![]() across the line
across the line ![]() to produce
to produce ![]() , we have that
, we have that ![]() . Since
. Since ![]() ,
, ![]() . Since
. Since ![]() , by the Pythagorean Theorem, our desired solution is just
, by the Pythagorean Theorem, our desired solution is just ![]() .
Looking next to circle arcs, we know that
.
Looking next to circle arcs, we know that ![]() , so
, so ![]() . Since
. Since ![]() , and
, and ![]() ,
, ![]() . Thus,
. Thus, ![]() .
Since
.
Since ![]() , by the Pythagorean Theorem, the desired
, by the Pythagorean Theorem, the desired ![]() .
.
~sofas103
Solution 5 (Basically Solution 2 With Motivation)
Basically, by PoP, you have that ![]() Therefore, as
Therefore, as ![]() basically, once you find
basically, once you find ![]() the problem is done. Now, this is an IMPORTANT concept: If you have a circle which you know the radius of and you want to find the length of a chord of that circle, drop an altitude from the center of the circle to the chord to find distance between the center of the circle and the chord.
the problem is done. Now, this is an IMPORTANT concept: If you have a circle which you know the radius of and you want to find the length of a chord of that circle, drop an altitude from the center of the circle to the chord to find distance between the center of the circle and the chord.
In this case, let ![]() be the midpoint of chord
be the midpoint of chord ![]() Notice that now we can use our
Notice that now we can use our ![]() angle, since
angle, since ![]() is a
is a ![]() triangle so that
triangle so that ![]() and
and ![]() However, we have that
However, we have that ![]() so that
so that ![]() Now, notice that
Now, notice that ![]() so that
so that ![]() and
and ![]() Therefore,
Therefore, ![]()
This may not be the “shortest solution”, but in my opinion is very well motivated and doesn’t require much creativity. [Not requiring much creativity, it also saves more time than you’d think. ;)]
~ Professor-Mom
Solution 6 (Double Power of a Point)
![[asy] /* Made by sofas103; edited by MRENTHUSIASM */ size(250); pair O, A, B, C, D, E, P, Q; O = origin; A = (-5*sqrt(2),0); B = (5*sqrt(2),0); E = (5*sqrt(2)-2*sqrt(5),0); P = (5*sqrt(2), -4.5); Q=(5*sqrt(2)-2*sqrt(5)-0.5, 0); path p; p = Circle(O,5*sqrt(2)); C = intersectionpoint(p,E--E+10*dir(135)); D = intersectionpoint(p,E--E+10*dir(-45)); draw(p); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$E$",E,1.5*dir(180+135/2),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); dot("$P$",P,1.5*dir(P),linewidth(4)); label("$45^{\circ}$",Q,NW); draw(A--B^^C--P--B); draw((5*sqrt(2), 0)--(5*sqrt(2)-0.4, 0)--(5*sqrt(2)-0.4, -0.4)--(5*sqrt(2), -0.4)); [/asy]](http://latex.artofproblemsolving.com/9/a/9/9a9728bef27f65e164a6891b192ef5fe033b7fc4.png) For ease of notation, let
For ease of notation, let ![]() and
and ![]() .
Extend
.
Extend ![]() to point
to point ![]() until
until ![]() is perpendicular to
is perpendicular to ![]() . It's given that
. It's given that ![]() , so, by vertical angles, we have
, so, by vertical angles, we have ![]() .
.
Since ![]() is a
is a ![]() right triangle, we have
right triangle, we have ![]() and
and ![]() . Hence,
. Hence, ![]()
By Power of a Point, we have
![]()
![]()
Isolating the variables after expanding gives ![]()
Using Power of a Point again, we have
![]()
![]()
![]() To get
To get ![]() , we can perform the operation
, we can perform the operation ![]() . Plugging these values in,
. Plugging these values in,
![]()
![]()
-Benedict T (countmath1)
Solution 7 (Cheating)
Perhaps not reliable in general, but very useful as a last resort.
The choice of the radius ![]() is strange, and is probably motivated by a nice answer in the end, so we only consider integer options. Notice that a 5 also appears in the condition
is strange, and is probably motivated by a nice answer in the end, so we only consider integer options. Notice that a 5 also appears in the condition ![]() , therefore it will likely be present in the answer as well; the only integer containing a factor of 5 amongst the choices is 100, thus the answer is
, therefore it will likely be present in the answer as well; the only integer containing a factor of 5 amongst the choices is 100, thus the answer is ![]()
~Maths357
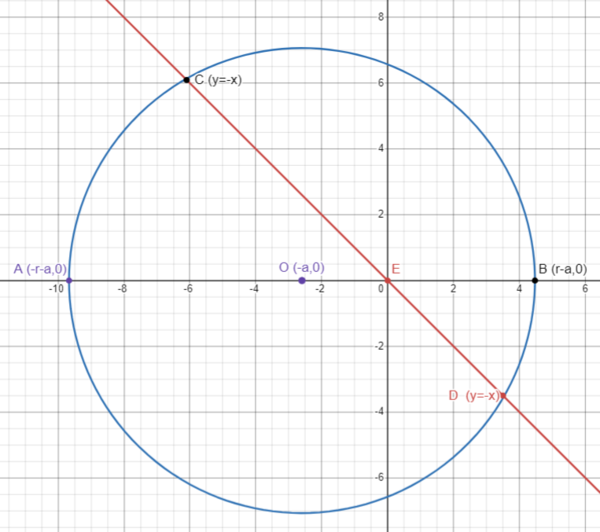
Solution 7 (Coordinate Geometry + Vieta)
set the origin at E (instead of circle center O) will reduce calculation.
line CD is y= -x ,
let OE = a , circle radius r=![]() ,
circle
,
circle ![]() intersects line y = -x at 2 points
intersects line y = -x at 2 points ![]() and
and ![]()
![]() ,
, ![]()
substitute y with x , circle becomes ![]()
![]() will be 2 roots of above quadratic and we will apply vieta
will be 2 roots of above quadratic and we will apply vieta ![]() below
below
![]()
plug in a = OE = OB - OE = ![]() and
and ![]() we get answer
we get answer ![]() .
.
Video Solution by OmegaLearn
https://youtu.be/HIPZ3nj_sT8?t=227
~ pi_is_3.14
Video Solution by On The Spot STEM
https://www.youtube.com/watch?v=h-hhRa93lK4
Video Solution by TheBeautyOfMath
See Also
| 2020 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 11 |
Followed by Problem 13 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()