2021 AMC 10B Problems/Problem 23
Contents
[hide]Problem
A square with side length ![]() is colored white except for
is colored white except for ![]() black isosceles right triangular regions with legs of length
black isosceles right triangular regions with legs of length ![]() in each corner of the square and a black diamond with side length
in each corner of the square and a black diamond with side length ![]() in the center of the square, as shown in the diagram. A circular coin with diameter
in the center of the square, as shown in the diagram. A circular coin with diameter ![]() is dropped onto the square and lands in a random location where the coin is completely contained within the square. The probability that the coin will cover part of the black region of the square can be written as
is dropped onto the square and lands in a random location where the coin is completely contained within the square. The probability that the coin will cover part of the black region of the square can be written as ![]() , where
, where ![]() and
and ![]() are positive integers. What is
are positive integers. What is ![]() ?
?
![[asy] /* Made by samrocksnature */ draw((0,0)--(8,0)--(8,8)--(0,8)--(0,0)); fill((2,0)--(0,2)--(0,0)--cycle, black); fill((6,0)--(8,0)--(8,2)--cycle, black); fill((8,6)--(8,8)--(6,8)--cycle, black); fill((0,6)--(2,8)--(0,8)--cycle, black); fill((4,6)--(2,4)--(4,2)--(6,4)--cycle, black); filldraw(circle((2.6,3.31),0.5),gray); [/asy]](http://latex.artofproblemsolving.com/f/7/f/f7f338e16788e51acc32f82a10daf271c5a104aa.png)
![]()
Diagram
Note that the center of the coin can lie anywhere inside a green region, as shown below.
![[asy] /* Made by MRENTHUSIASM */ draw((0,0)--(8,0)--(8,8)--(0,8)--(0,0)); fill((2,0)--(0,2)--(0,0)--cycle, black); fill((6,0)--(8,0)--(8,2)--cycle, black); fill((8,6)--(8,8)--(6,8)--cycle, black); fill((0,6)--(2,8)--(0,8)--cycle, black); fill((4,6)--(2,4)--(4,2)--(6,4)--cycle, black); draw((0.5,7.5)--(0.5+1+sqrt(2)/2,7.5)--(0.5,7.5-1-sqrt(2)/2)--cycle, green); draw((0.5,0.5)--(0.5+1+sqrt(2)/2,0.5)--(0.5,0.5+1+sqrt(2)/2)--cycle, green); draw((7.5,7.5)--(7.5-1-sqrt(2)/2,7.5)--(7.5,7.5-1-sqrt(2)/2)--cycle, green); draw((7.5,0.5)--(7.5-1-sqrt(2)/2,0.5)--(7.5,0.5+1+sqrt(2)/2)--cycle, green); draw(Arc((4,6),0.5,135,45)--Arc((6,4),0.5,45,-45)--Arc((4,2),0.5,-45,-135)--Arc((2,4),0.5,225,135)--cycle, green); [/asy]](http://latex.artofproblemsolving.com/8/0/d/80de1b87bb354410fd58b705ace2bcf031ec62f3.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution
To find the probability, we look at the ![]() . For the coin to be completely contained within the square, we must have the distance from the center of the coin to a side of the square to be at least
. For the coin to be completely contained within the square, we must have the distance from the center of the coin to a side of the square to be at least ![]() , as it's the radius of the coin. This implies the
, as it's the radius of the coin. This implies the ![]() is a square with side length
is a square with side length ![]() , with an area of
, with an area of ![]() . Now, we consider cases where needs to land to partially cover a black region.
. Now, we consider cases where needs to land to partially cover a black region.
Near The Center Square
We can have the center of the coin land within ![]() outside of the center square, or inside of the center square. So, we have a region with
outside of the center square, or inside of the center square. So, we have a region with ![]() emanating from every point on the exterior of the square, forming four quarter circles and four rectangles. The four quarter circles combine to make a full circle of radius
emanating from every point on the exterior of the square, forming four quarter circles and four rectangles. The four quarter circles combine to make a full circle of radius ![]() , so the area is
, so the area is ![]() . The area of a rectangle is
. The area of a rectangle is ![]() , so
, so ![]() of them combine to an area of
of them combine to an area of ![]() . The area of the black square is simply
. The area of the black square is simply ![]() . So, for this case, we have a combined total of
. So, for this case, we have a combined total of ![]() . Onto the second (and last) case.
. Onto the second (and last) case.
Near A Triangle
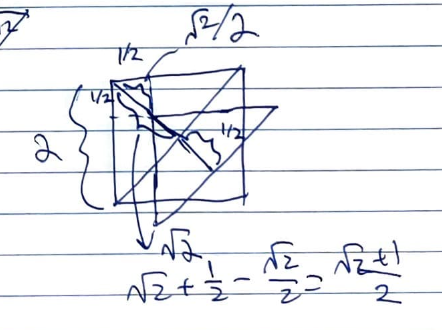
We can also have the coin land within ![]() outside of one of the triangles. By symmetry, we can just find the successful region for one of them, then multiply by
outside of one of the triangles. By symmetry, we can just find the successful region for one of them, then multiply by ![]() . Consider the above diagram. We can draw an altitude from the bottom corner of the square to hit the hypotenuse of the green triangle. The length of this when passing through the black region is
. Consider the above diagram. We can draw an altitude from the bottom corner of the square to hit the hypotenuse of the green triangle. The length of this when passing through the black region is ![]() , and when passing through the white region (while being contained in the green triangle) is
, and when passing through the white region (while being contained in the green triangle) is ![]() . However, we have to subtract off when it doesn't pass through the red square. Then, it's the hypotenuse of a small isosceles right triangle with side lengths of
. However, we have to subtract off when it doesn't pass through the red square. Then, it's the hypotenuse of a small isosceles right triangle with side lengths of ![]() which is
which is ![]() So, the altitude of the green triangle is
So, the altitude of the green triangle is ![]() . Then, recall, the area of an isosceles right triangle is
. Then, recall, the area of an isosceles right triangle is ![]() , where
, where ![]() is the altitude from the right angle. So, squaring this, we get
is the altitude from the right angle. So, squaring this, we get ![]() . Now, we have to multiply this by
. Now, we have to multiply this by ![]() to account for all of the black triangles, to get
to account for all of the black triangles, to get ![]() as the final area for this case.
as the final area for this case.
Finishing
Then, to have the coin touching a black region, we add up the area of our successful regions, or ![]() . The total region is
. The total region is ![]() , so our probability is
, so our probability is ![]() , which implies
, which implies ![]() . This corresponds to answer choice
. This corresponds to answer choice ![]() .
.
~rocketsri ~ minor edit from jrepsa ~ minor edit from lpieleanu
Image
~mathboy282
Video Solution by OmegaLearn (Similar Triangles and Area Calculations)
~ pi_is_3.14
Video Solution by Interstigation (Using Casework)
~ Interstigation
Video Solution by The Power of Logic
https://www.youtube.com/watch?v=o3_kUpWUokw
See Also
| 2021 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()