2022 AIME I Problems/Problem 5
Contents
[hide]Problem
A straight river that is ![]() meters wide flows from west to east at a rate of
meters wide flows from west to east at a rate of ![]() meters per minute. Melanie and Sherry sit on the south bank of the river with Melanie a distance of
meters per minute. Melanie and Sherry sit on the south bank of the river with Melanie a distance of ![]() meters downstream from Sherry. Relative to the water, Melanie swims at
meters downstream from Sherry. Relative to the water, Melanie swims at ![]() meters per minute, and Sherry swims at
meters per minute, and Sherry swims at ![]() meters per minute. At the same time, Melanie and Sherry begin swimming in straight lines to a point on the north bank of the river that is equidistant from their starting positions. The two women arrive at this point simultaneously. Find
meters per minute. At the same time, Melanie and Sherry begin swimming in straight lines to a point on the north bank of the river that is equidistant from their starting positions. The two women arrive at this point simultaneously. Find ![]() .
.
Solution 1 (Euclidean)
Define ![]() as the number of minutes they swim for.
as the number of minutes they swim for.
Let their meeting point be ![]() . Melanie is swimming against the current, so she must aim upstream from point
. Melanie is swimming against the current, so she must aim upstream from point ![]() , to compensate for this; in particular, since she is swimming for
, to compensate for this; in particular, since she is swimming for ![]() minutes, the current will push her
minutes, the current will push her ![]() meters downstream in that time, so she must aim for a point
meters downstream in that time, so she must aim for a point ![]() that is
that is ![]() meters upstream from point
meters upstream from point ![]() . Similarly, Sherry is swimming downstream for
. Similarly, Sherry is swimming downstream for ![]() minutes, so she must also aim at point
minutes, so she must also aim at point ![]() to compensate for the flow of the current.
to compensate for the flow of the current.
If Melanie and Sherry were to both aim at point ![]() in a currentless river with the same dimensions, they would still both meet at that point simultaneously. Since there is no current in this scenario, the distances that Melanie and Sherry travel, respectively, are
in a currentless river with the same dimensions, they would still both meet at that point simultaneously. Since there is no current in this scenario, the distances that Melanie and Sherry travel, respectively, are ![]() and
and ![]() meters. We can draw out this new scenario, with the dimensions that we have:
meters. We can draw out this new scenario, with the dimensions that we have:
![[asy] unitsize(0.02cm); draw((0,0)--(0,264)--(550,264)--(550,0)--cycle); pair B = (198,264); dot(B^^(0,0)^^(550,0),linewidth(5)); draw((0,0)--B,dashed); draw((550,0)--B,dashed); label("$60m$", (0,0)--B, E); label("$80m$", (550,0)--B, W); label("$264$", (0,0)--(0,264), W); label("$\frac{D}{2} - 14m$", (0,264)--B, N); label("$\frac{D}{2} + 14m$", B--(550,264), N); label("$D$", (0,0)--(550,0), S); label("$B$", B, N); label("Downstream", (350,325), E); label("Upstream", (200,325), W); draw((225,325)--(325,325), Arrows); [/asy]](http://latex.artofproblemsolving.com/c/9/8/c98f18cb73b2f89c7bcb2b9b69cb850de8edb86b.png) (While it is indeed true that the triangle above with side lengths
(While it is indeed true that the triangle above with side lengths ![]() ,
, ![]() and
and ![]() is a right triangle, we do not know this yet, so we cannot assume this based on the diagram.)
is a right triangle, we do not know this yet, so we cannot assume this based on the diagram.)
By the Pythagorean Theorem, we have

Subtracting the first equation from the second gives us ![]() , so
, so ![]() . Substituting this into our first equation, we have that
. Substituting this into our first equation, we have that

So ![]() .
.
~ihatemath123
Solution 2 (Euclidean)
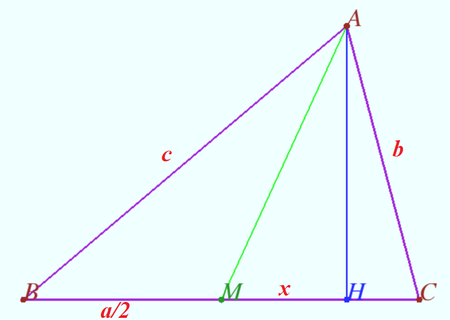
Claim
Median ![]() and altitude
and altitude ![]() are drawn in triangle
are drawn in triangle ![]() .
.
![]() are known. Let's denote
are known. Let's denote ![]() .
.
Prove that
![]()
Proof
![]()
![]()
![]()
![]()
Solution
In the coordinate system associated with water, the movement is described by the scheme in the form of a triangle, the side on which Melanie floats is ![]() , where t is the time of Melanie's movement, the side along which Sherry floats is
, where t is the time of Melanie's movement, the side along which Sherry floats is ![]() .
.
The meeting point floated away at a distance of ![]() from the midpoint between the starting points of Melanie and Sherry.
from the midpoint between the starting points of Melanie and Sherry.
In the notation of the Claim,
![]() Hence,
Hence,
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 3 (Vectors)
We have the following diagram:
![[asy] /* Made by MRENTHUSIASM */ size(350); pair A, B, C; A = (0,264); B = (-275,0); C = (275,0); draw((-300,0)--(300,0)^^(-300,264)--(300,264)^^A--B^^A--C,linewidth(2)); dot("Finish",A,1.75*N,linewidth(5)); dot("Sherry",B,1.75*S,linewidth(5)); dot("Melanie",C,1.75*S,linewidth(5)); Label L1 = Label("$D$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); Label L2 = Label("$264$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); Label L3 = Label("Current $(14)$", position=EndPoint, filltype=Fill(3,0,white)); Label L4 = Label("$y$", align=(-1,0), position=Relative(0.4)); Label L5 = Label("$x$", align=(0,1), position=Relative(0.4)); Label L6 = Label("$y$", align=(1,0), position=Relative(0.4)); Label L7 = Label("$x$", align=(0,1), position=Relative(0.4)); draw(B-(0,75)--C-(0,75), L=L1, arrow=Arrows(),bar=Bars(15)); draw((-350,0)--(-350,264), L=L2, arrow=Arrows(),bar=Bars(15)); draw((-300,-120)--(300,-120), L=L3, arrow=EndArrow()); draw(B--B+(0,48), L=L4, arrow=EndArrow()); draw(B+(0,48)--B+(50,48), L=L5, arrow=EndArrow()); draw(C--C+(0,48), L=L6, arrow=EndArrow()); draw(C+(0,48)--C+(-50,48), L=L7, arrow=EndArrow()); [/asy]](http://latex.artofproblemsolving.com/4/b/3/4b3778bd6360db7b8a07bde0da72601a8ef76df3.png) Since Melanie and Sherry swim for the same distance and the same amount of time, they swim at the same net speed.
Since Melanie and Sherry swim for the same distance and the same amount of time, they swim at the same net speed.
Let ![]() and
and ![]() be some positive numbers. We have the following table:
be some positive numbers. We have the following table:
![\[\begin{array}{c||c|c|c} & \textbf{Net Velocity Vector (m/min)} & \textbf{Natural Velocity Vector (m/min)} & \textbf{Natural Speed (m/min)} \\ \hline \hline &&& \\ [-2.25ex] \textbf{Melanie} & \langle -x,y\rangle & \langle -x-14,y\rangle & 80 \\ \hline &&& \\ [-2.25ex] \textbf{Sherry} & \langle x,y\rangle & \langle x-14,y\rangle & 60 \end{array}\]](http://latex.artofproblemsolving.com/4/4/7/4474c673afba6a121cd1fc59a0c1d7f206d1427d.png) Recall that
Recall that ![]() so
so
![]() We subtract
We subtract ![]() from
from ![]() to get
to get ![]() from which
from which ![]() Substituting this into either equation, we have
Substituting this into either equation, we have ![]()
It follows that Melanie and Sherry both swim for ![]() minutes. Therefore, the answer is
minutes. Therefore, the answer is ![]() ~MRENTHUSIASM
~MRENTHUSIASM
Solution 4 (Vectors)
We can break down movement into two components: the ![]() -component and the
-component and the ![]() -component. Suppose that Melanie travels a distance of
-component. Suppose that Melanie travels a distance of ![]() in the
in the ![]() -direction and a distance of
-direction and a distance of ![]() in the
in the ![]() -direction in one minute when there is no current. Similarly, suppose that Sherry travels a distance of
-direction in one minute when there is no current. Similarly, suppose that Sherry travels a distance of ![]() in the
in the ![]() -direction but a distance of
-direction but a distance of ![]() in the
in the ![]() -direction in one minute when there is no current. The current only affects the
-direction in one minute when there is no current. The current only affects the ![]() -components because it goes in the
-components because it goes in the ![]() -direction.
-direction.
![[asy] /* Ruthlessly plagiarized from MRENTHUSIASM by Curious_crow */ size(350); pair A, B, C; A = (0,264); B = (-275,0); C = (275,0); draw((-300,0)--(300,0)^^(-300,264)--(300,264)^^A--B^^A--C,linewidth(2)); dot("Finish",A,1.75*N,linewidth(5)); dot("Sherry",B,1.75*S,linewidth(5)); dot("Melanie",C,1.75*S,linewidth(5)); Label L1 = Label("$D$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); Label L2 = Label("$264$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); Label L3 = Label("Current $(14)$", position=EndPoint, filltype=Fill(3,0,white)); Label L4 = Label("$a$", align=(-1,0), position=Relative(0.4)); Label L5 = Label("$b+14$", align=(0,1), position=Relative(0.4)); Label L6 = Label("$a$", align=(1,0), position=Relative(0.4)); Label L7 = Label("$c-14$", align=(0,1), position=Relative(0.4)); draw(B-(0,75)--C-(0,75), L=L1, arrow=Arrows(),bar=Bars(15)); draw((-350,0)--(-350,264), L=L2, arrow=Arrows(),bar=Bars(15)); draw((-300,-120)--(300,-120), L=L3, arrow=EndArrow()); draw(B--B+(0,48), L=L4, arrow=EndArrow()); draw(B+(0,48)--B+(50,48), L=L5, arrow=EndArrow()); draw(C--C+(0,48), L=L6, arrow=EndArrow()); draw(C+(0,48)--C+(-50,48), L=L7, arrow=EndArrow()); [/asy]](http://latex.artofproblemsolving.com/3/7/c/37c61de2f303ab9b5f83d1fd28879d3a22d2e36e.png)
Now, note that ![]() because Sherry travels 60 meters in a minute. Thus,
because Sherry travels 60 meters in a minute. Thus, ![]() because Melanie travels 80 meters in a minute. Also, the distance they travel with the current must be the same in one minute because they reach the point equidistant from them at the same time. That means
because Melanie travels 80 meters in a minute. Also, the distance they travel with the current must be the same in one minute because they reach the point equidistant from them at the same time. That means ![]() or
or ![]() . So now we can plug that into the two equations to get:
. So now we can plug that into the two equations to get:
![]() We can solve the system of equations to get
We can solve the system of equations to get ![]() and
and ![]() . From this, we can figure out that it must've taken them
. From this, we can figure out that it must've taken them ![]() minutes to get to the other side, because
minutes to get to the other side, because ![]() . This means that there are
. This means that there are ![]() lengths of
lengths of ![]() in each person's travel. Also,
in each person's travel. Also, ![]() must be equal to
must be equal to ![]() because there are
because there are ![]() lengths of
lengths of ![]() between them,
between them, ![]() on each person's side. Since
on each person's side. Since ![]() , we have
, we have ![]() , so the answer is
, so the answer is ![]() ~Curious_crow
~Curious_crow
Video Solution 1
https://youtu.be/MJ_M-xvwHLk?t=1487
~ThePuzzlr
Video Solution 2
https://www.youtube.com/watch?v=s6nXXnBLTdA
~Chickenugget
Video Solution 3
~AMC & AIME Training
See Also
| 2022 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||