2022 AIME I Problems/Problem 8
Contents
[hide]Problem
Equilateral triangle ![]() is inscribed in circle
is inscribed in circle ![]() with radius
with radius ![]() Circle
Circle ![]() is tangent to sides
is tangent to sides ![]() and
and ![]() and is internally tangent to
and is internally tangent to ![]() Circles
Circles ![]() and
and ![]() are defined analogously. Circles
are defined analogously. Circles ![]()
![]() and
and ![]() meet in six points---two points for each pair of circles. The three intersection points closest to the vertices of
meet in six points---two points for each pair of circles. The three intersection points closest to the vertices of ![]() are the vertices of a large equilateral triangle in the interior of
are the vertices of a large equilateral triangle in the interior of ![]() and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of
and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of ![]() The side length of the smaller equilateral triangle can be written as
The side length of the smaller equilateral triangle can be written as ![]() where
where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(250); pair A, B, C, W, WA, WB, WC, X, Y, Z; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$\omega$",W,1.5*dir(270),linewidth(4)); dot("$\omega_A$",WA,1.5*dir(-WA),linewidth(4)); dot("$\omega_B$",WB,1.5*dir(-WB),linewidth(4)); dot("$\omega_C$",WC,1.5*dir(-WC),linewidth(4)); [/asy]](http://latex.artofproblemsolving.com/7/b/e/7bea64b6b313d0e3cb3876a8dce7a5e31fb53bc5.png) ~MRENTHUSIASM ~ihatemath123
~MRENTHUSIASM ~ihatemath123
Solution 1 (Coordinate Geometry)
We can extend ![]() and
and ![]() to
to ![]() and
and ![]() respectively such that circle
respectively such that circle ![]() is the incircle of
is the incircle of ![]() .
.
![[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, B1, C1, W, WA, WB, WC, X, Y, Z; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); B1 = A+24*sqrt(3)*dir(B-A); C1 = A+24*sqrt(3)*dir(C-A); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); draw(B--B1--C1--C,dashed); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*(-1,0),linewidth(4)); dot("$C$",C,1.5*(1,0),linewidth(4)); dot("$B'$",B1,1.5*dir(B1),linewidth(4)); dot("$C'$",C1,1.5*dir(C1),linewidth(4)); dot("$O$",W,1.5*dir(90),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); [/asy]](http://latex.artofproblemsolving.com/7/6/f/76f54940dcd74766c15bdfe4a4622e77c010dc2e.png) Since the diameter of the circle is the height of this triangle, the height of this triangle is
Since the diameter of the circle is the height of this triangle, the height of this triangle is ![]() . We can use inradius or equilateral triangle properties to get the inradius of this triangle is
. We can use inradius or equilateral triangle properties to get the inradius of this triangle is ![]() (The incenter is also a centroid in an equilateral triangle, and the distance from a side to the centroid is a third of the height). Therefore, the radius of each of the smaller circles is
(The incenter is also a centroid in an equilateral triangle, and the distance from a side to the centroid is a third of the height). Therefore, the radius of each of the smaller circles is ![]() .
.
Let ![]() be the center of the largest circle. We will set up a coordinate system with
be the center of the largest circle. We will set up a coordinate system with ![]() as the origin. The center of
as the origin. The center of ![]() will be at
will be at ![]() because it is directly beneath
because it is directly beneath ![]() and is the length of the larger radius minus the smaller radius, or
and is the length of the larger radius minus the smaller radius, or ![]() . By rotating this point
. By rotating this point ![]() around
around ![]() , we get the center of
, we get the center of ![]() . This means that the magnitude of vector
. This means that the magnitude of vector ![]() is
is ![]() and is at a
and is at a ![]() degree angle from the horizontal. Therefore, the coordinates of this point are
degree angle from the horizontal. Therefore, the coordinates of this point are ![]() and by symmetry the coordinates of the center of
and by symmetry the coordinates of the center of ![]() is
is ![]() .
.
The upper left and right circles intersect at two points, the lower of which is ![]() . The equations of these two circles are:
. The equations of these two circles are:
 We solve this system by subtracting to get
We solve this system by subtracting to get ![]() . Plugging back in to the first equation, we have
. Plugging back in to the first equation, we have ![]() . Since we know
. Since we know ![]() is the lower solution, we take the negative value to get
is the lower solution, we take the negative value to get ![]() .
.
We can solve the problem two ways from here. We can find ![]() by rotation and use the distance formula to find the length, or we can be somewhat more clever. We notice that it is easier to find
by rotation and use the distance formula to find the length, or we can be somewhat more clever. We notice that it is easier to find ![]() as they lie on the same vertical,
as they lie on the same vertical, ![]() is
is ![]() degrees so we can make use of
degrees so we can make use of ![]() triangles, and
triangles, and ![]() because
because ![]() is the center of triangle
is the center of triangle ![]() . We can draw the diagram as such:
. We can draw the diagram as such:
![[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, B1, C1, W, WA, WB, WC, X, Y, Z; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); B1 = A+24*sqrt(3)*dir(B-A); C1 = A+24*sqrt(3)*dir(C-A); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); draw(B--B1--C1--C^^W--X^^W--Y^^W--midpoint(X--Y),dashed); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*(-1,0),linewidth(4)); dot("$C$",C,1.5*(1,0),linewidth(4)); dot("$B'$",B1,1.5*dir(B1),linewidth(4)); dot("$C'$",C1,1.5*dir(C1),linewidth(4)); dot("$O$",W,1.5*dir(90),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); [/asy]](http://latex.artofproblemsolving.com/d/9/3/d93cd11d7b2c2112ec72b5271f4e84a73bd42996.png) Note that
Note that ![]() . It follows that
. It follows that
 Finally, the answer is
Finally, the answer is ![]() .
.
~KingRavi
Solution 2 (Euclidean Geometry)
![[asy] /* Made by MRENTHUSIASM */ /* Modified by isabelchen */ size(250); pair A, B, C, W, WA, WB, WC, X, Y, Z, D, E; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); D = intersectionpoint(Circle(WA,12),A--C); E = intersectionpoints(Circle(WB,12),Circle(WC,12))[0]; filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$\omega$",W,1.5*dir(270),linewidth(4)); dot("$\omega_A$",WA,1.5*dir(-WA),linewidth(4)); dot("$\omega_B$",WB,1.5*dir(-WB),linewidth(4)); dot("$\omega_C$",WC,1.5*dir(-WC),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); dot("$E$",E,1.5*dir(E),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); draw(WC--WB^^WC--X^^WC--E^^WA--D^^A--X); [/asy]](http://latex.artofproblemsolving.com/1/a/3/1a39ebb8a6f7875abffc117c37c6fbf073c10461.png) For equilateral triangle with side length
For equilateral triangle with side length ![]() , height
, height ![]() , and circumradius
, and circumradius ![]() , there are relationships:
, there are relationships: ![]() ,
, ![]() , and
, and ![]() .
.
There is a lot of symmetry in the figure. The radius of the big circle ![]() is
is ![]() , let the radius of the small circles
, let the radius of the small circles ![]() ,
, ![]() ,
, ![]() be
be ![]() .
.
We are going to solve this problem in ![]() steps:
steps:
![]()
We have ![]() is a
is a ![]() triangle, and
triangle, and ![]() ,
, ![]() (
(![]() and
and ![]() are tangent), and
are tangent), and ![]() . So, we get
. So, we get ![]() and
and ![]() .
.
Since ![]() and
and ![]() are tangent, we get
are tangent, we get ![]() .
.
Note that ![]() is an equilateral triangle, and
is an equilateral triangle, and ![]() is its center, so
is its center, so ![]() .
.
![]()
Note that ![]() is an isosceles triangle, so
is an isosceles triangle, so ![]()
![]()
In ![]() , Power of a Point gives
, Power of a Point gives ![]() and
and ![]() .
.
It follows that ![]() . We solve this quadratic equation:
. We solve this quadratic equation: ![]() .
.
Since ![]() is the circumradius of equilateral
is the circumradius of equilateral ![]() , we have
, we have ![]() .
.
Therefore, the answer is ![]() .
.
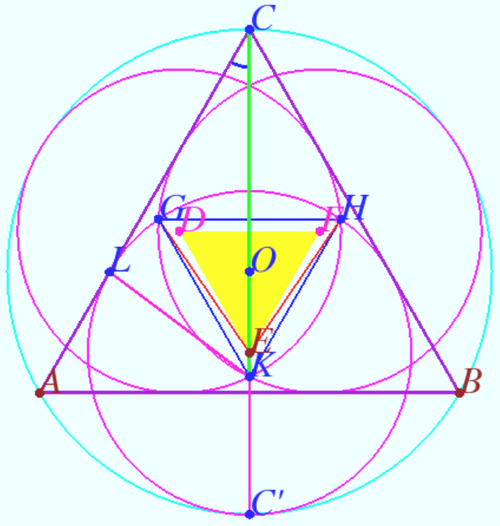
Solution 3 (Simple Geometry)
Let ![]() be the center,
be the center, ![]() be the radius, and
be the radius, and ![]() be the diameter of
be the diameter of ![]() Let
Let ![]() be the radius,
be the radius, ![]() are the centers of
are the centers of ![]() Let
Let ![]() be the desired triangle with side
be the desired triangle with side ![]() We find
We find ![]() using
using
![]()
![]()
![]() Triangles
Triangles ![]() and
and ![]() – are equilateral triangles with a common center
– are equilateral triangles with a common center ![]() therefore in the triangle
therefore in the triangle ![]()
![]()
We apply the Law of Cosines to ![]() and get
and get
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 4 (Mixtilinear Incircles)
Let ![]() be the center of
be the center of ![]() ,
, ![]() be the intersection of
be the intersection of ![]() further from
further from ![]() , and
, and ![]() be the center of
be the center of ![]() . Define
. Define ![]() similarly. It is well-known that the
similarly. It is well-known that the ![]() -mixtilinear inradius
-mixtilinear inradius ![]() is
is ![]() , so in particular this means that
, so in particular this means that ![]() . Since
. Since ![]() , it follows by Law of Cosines on
, it follows by Law of Cosines on ![]() that
that ![]() . Then the Pythagorean theorem gives that the altitude of
. Then the Pythagorean theorem gives that the altitude of ![]() is
is ![]() , so
, so ![]() and
and ![]() so the answer is
so the answer is ![]() .
.
~Kagebaka
Video Solution
~MathProblemSolvingSkills.com
Video Solution
~AMC & AIME Training
See Also
| 2022 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()