2023 AMC 12B Problems/Problem 7
Contents
[hide]Problem
For how many integers ![]() does the expression
does the expression![\[\sqrt{\frac{\log (n^2) - (\log n)^2}{\log n - 3}}\]](http://latex.artofproblemsolving.com/d/c/b/dcb19417f3c2ddfd1ca85657b18676af13834b8a.png) represent a real number, where log denotes the base
represent a real number, where log denotes the base ![]() logarithm?
logarithm?
![]()
Solution
We have

Because ![]() is an integer and
is an integer and ![]() is well defined,
is well defined, ![]() must be a positive integer.
must be a positive integer.
Case 1: ![]() or
or ![]() .
.
The above expression is 0. So these are valid solutions.
Case 2: ![]() .
.
Thus, ![]() and
and ![]() .
To make the above expression real, we must have
.
To make the above expression real, we must have ![]() .
Thus,
.
Thus, ![]() .
Thus,
.
Thus, ![]() .
Hence, the number of solutions in this case is 899.
.
Hence, the number of solutions in this case is 899.
Putting all cases together, the total number of solutions is
![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution (Solution 1 Simplified)
Notice ![]() can be written as
can be written as ![]() . Setting
. Setting ![]() , the equation becomes
, the equation becomes ![]() which can be written as
which can be written as 
Case 1: ![]() The expression is undefined when
The expression is undefined when ![]() . For
. For ![]() , it is trivial to see that the denominator is positive and the numerator is negative, thus resulting in no real solutions.
, it is trivial to see that the denominator is positive and the numerator is negative, thus resulting in no real solutions.
Case 2: ![]() For
For ![]() , the numerator is zero, giving us a valid solution. When
, the numerator is zero, giving us a valid solution. When ![]() , both the denominator and numerator are negative so all real values of a in this interval is a solution to the equation. All integers of n that makes this true are between
, both the denominator and numerator are negative so all real values of a in this interval is a solution to the equation. All integers of n that makes this true are between ![]() and
and ![]() . There are 900 solutions here.
. There are 900 solutions here.
Case 3: ![]() The numerator will be positive but the denominator is negative, no real solutions exist.
The numerator will be positive but the denominator is negative, no real solutions exist.
Case 4: ![]() The expression evaluates to zero,
The expression evaluates to zero, ![]() valid solution exists.
valid solution exists.
Case 5: ![]() All values for
All values for ![]() requires
requires ![]() , no integer solutions exist.
, no integer solutions exist.
Adding up the cases:
![]()
~woeIsMe typesetting: paras
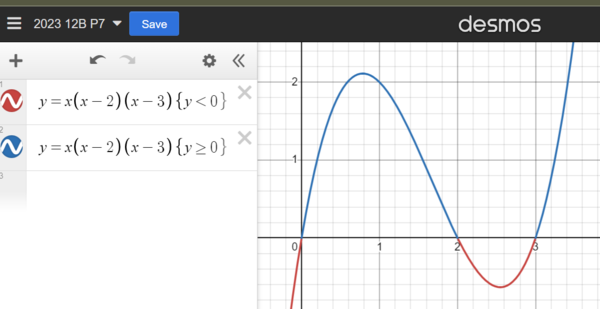
Solution 3 (3 degree polynominal graph)
for ![]() ,
,
transform it into a(a-2)(a-3) <0 ,
use the following graph to quickly confirm
1) a < 0 or
2) 2 < a <3
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
See Also
| 2023 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 6 |
Followed by Problem 8 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()