2023 AMC 12B Problems/Problem 25

The following problem is from both the 2023 AMC 10B #25 and 2023 AMC 12B #25, so both problems redirect to this page.

1 Problem
2 Solution 1
- 2.1 Option 1: Knowledge
- 2.2 Option 2: Angle Identities
3 Solution 2
4 Solution 3
5 Solution 4
6 Solution 5 (answer choices (not rigorous))
7 Supplement (Calculating sin54/cos36 from Scratch)
8 Video Solution 1 by SpreadTheMathLove
9 Video Solution 2 by OmegaLearn
10 Video Solution
11 See also

Problem

A regular pentagon with area $\sqrt{5}+1$ is printed on paper and cut out. The five vertices of the pentagon are folded into the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon?

$\textbf{(A)}~4-\sqrt{5}\qquad\textbf{(B)}~\sqrt{5}-1\qquad\textbf{(C)}~8-3\sqrt{5}\qquad\textbf{(D)}~\frac{\sqrt{5}+1}{2}\qquad\textbf{(E)}~\frac{2+\sqrt{5}}{3}$

Solution 1

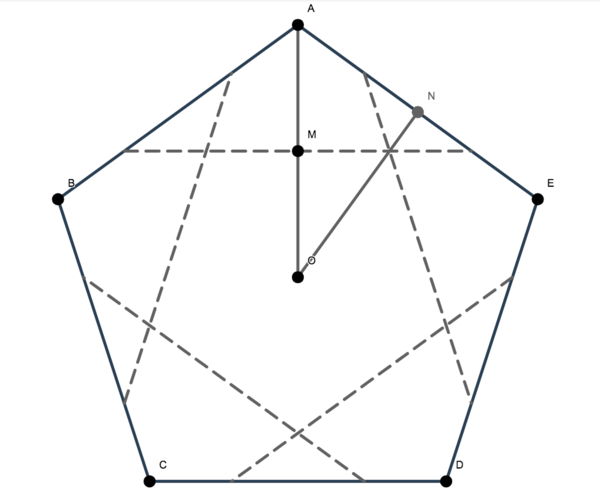
Let the original pentagon be $ABCDE$ centered at $O$ . The dashed lines represent the fold lines. WLOG, let's focus on vertex $A$ .

Since $A$ is folded onto $O$ , $AM = MO$ where $M$ is the intersection of $AO$ and the creaseline between $A$ and $O$ . Note that the inner pentagon is regular, and therefore similar to the original pentagon, due to symmetry.

Because of their similarity, the ratio of the inner pentagon's area to that of the outer pentagon can be represented by

$(\frac{OM}{ON})^{2} = (\frac{\frac{OA}{2}}{OA\sin (\angle OAE)})^{2} = \frac{1}{4\sin^{2}54}$

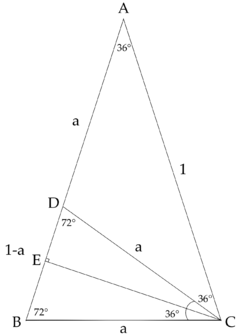
Option 1: Knowledge

Remember that $\sin54 = \frac{1+\sqrt5}{4}$ .

Option 2: Angle Identities

$\sin54 = \cos36$

$4\cos^{3}18-3\cos18 = 2\sin18\cos18$

$4(1-\sin^{2}18)-3-2\sin18=0$

$4\sin^{2}18+2\sin18-1=0$

$\sin18 = \frac{-1+\sqrt5}{4}$

$\sin54 = \cos36 = 1-2\sin^{2}18 = \frac{1+\sqrt5}{4}$

$\sin^{2}54 =\frac{3+\sqrt5}{8}$

Let the inner pentagon be $Z$ .

$[Z] = \frac{1}{4\sin^{2}54}[ABCDE]$

$= \frac{2(1+\sqrt5)}{3+\sqrt5}$

$= \sqrt5-1$

$\boxed{B}$

-Dissmo

Solution 2

$[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); // Draw the larger pentagon draw(A--B--C--D--E--cycle); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); label("$O$", O, S); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); dot(O); label("$A$", (0,1), E); label("$B$", B, S); label("$C$", C, S); label("$D$", D, S); label("$E$", E, W); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); pair K, L, M, N, O, P, Q, R, S, T, U, V; real newScaleFactor = 0.8507; K = newScaleFactor*dir(270+18); L = newScaleFactor*dir(270+72+18); M = newScaleFactor*dir(270+72+72+18); N = newScaleFactor*dir(270+72+72+72+18); O = newScaleFactor*dir(270+72+72+72+72+18); P = newScaleFactor*dir(270-18); Q = newScaleFactor*dir(270+72-18); R = newScaleFactor*dir(270+72+72-18); S = newScaleFactor*dir(270+72+72+72-18); T = newScaleFactor*dir(270+72+72+72+72-18); label("$K$", K, S); label("$L$", L, S); label("$M$", M, S); label("$N$", N, S); label("$O$", O, W); label("$P$", P, S); label("$Q$", Q, E); label("$R$", R, S); label("$S$", S, S); label("$T$", T, W); draw(K--T, dashed); draw(S--O, dashed); draw(P--L, dashed); draw(Q--M, dashed); draw(R--N, dashed); label("$F$", F, S); label("$G$", G, S); label("$H$", H, S); label("$I$", I, S); label("$J$", J, S); // Draw the smaller pentagon draw(F--G--H--I--J--cycle,red); [/asy]$

We can find the area of the red pentagon by taking the area of the total pentagon and subtracting the area outside the red pentagon.

The area outside the red pentagon is the sum of the larger isosceles triangles, but this double counts the overlapping regions of the small isosceles triangles, so we have to subtract those out.

We have $[FGHIJ] = [ABCDE]-(5 \cdot[DKT]-5 \cdot [PFK])$

Lets focus on finding the area of each individual triangle:

$[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); label("$O$", O, S); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); dot(O); label("$D$", D, S); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); label("$F$", F, N); pair K, L, M, N, O, P, Q, R, S, T, U, V; real newScaleFactor = 0.8507; K = newScaleFactor*dir(270+18); T = newScaleFactor*dir(270+72+72+72+72-18); label("$K$", K, E); label("$T$", T, W); draw(K--T); draw(K--D); draw(D--T); [/asy]$

Notice that we have no information about the side length, so instead we let the side length be $s$ . Now we can drop an altitude from $O$ to the base of the triangle, and we know this altitude must split the base of the pentagon in half, so we can create a right triangle. Furthermore, draw a line from $O$ to $D$ . This must bisect angle $D$ which is $108$ degrees, so we create $36-54-90$ triangles. Specifically, we know $\angle ODK = 54^{\circ}$ , $\angle DOU = 36^{\circ}$ , and $\angle DTK = 36^{\circ}$ because $\triangle DTK$ is isosceles and we know the vertex angle is $108^{\circ}$ . We encode this information in the diagram below: $[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); label("$O$", O, E); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); dot(O); label("$D$", D, S); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); label("$F$", (0.1,-1/1.618), E); pair K, L, M, N, O, P, Q, R, S, T, U, V; real newScaleFactor = 0.8507; K = newScaleFactor*dir(270+18); T = newScaleFactor*dir(270+72+72+72+72-18); label("$K$", K, S); label("$T$", T, W); draw(K--T); draw(K--D); draw(D--T); pair U; U=(0,-0.809); label("$U$",(0,-0.9), S); draw(O--U); draw(O--D); pair V; V = midpoint(O--D); label("$V$", V+(0,0.05), N); markscalefactor = 0.005; draw(rightanglemark(D,U,O)); draw(rightanglemark(F,V,O)); draw(rightanglemark(K,U,F)); draw(anglemark(U,D,O)); label("$54^{\circ}$", D+(0.05,0),NE); draw(anglemark(D,O,U)); label("$36^{\circ}$", O-(0,0.2),SW); draw(anglemark(D,T,F)); label("$36^{\circ}$", T+(0.1,-0.17),SE); label("$\frac{s}{2}$", D+(0.3,-0.1), S); [/asy]$

Since $\triangle DKT$ is isosceles, the area of $\triangle DVT$ is half the area of $\triangle DKT$ . Similarly, the area of $\triangle UFK$ is half that of $\triangle PFK$ . Thus:

$[FGHIJ] = [ABCDE]-(5 \cdot[DKT]-5 \cdot [PFK]) \implies [FGHIJ] = [ABCDE]-(10 \cdot [DVT]-10 \cdot [UFK])$

We also know that since we dropped an altitude from $O$ to $U$ , the area of $\triangle ODU$ must be half of a fifth of the total area of the pentagon. Therefore we can rewrite the above equation as $[FGHIJ]=10 \cdot ([ODU]-[DVT]+[UFK])$

Now notice that $\triangle ODU ~ \triangle TDV ~ \triangle KFU$ by AA similarity. Therefore, if we can write the areas of the latter two triangles as a ratio of the first triangle, we can express the whole equation in terms of $[ODU]$ , and by extension $[ABCDE]$ , which we know. To find these ratios, we can find the side length ratios and square them because the triangles are similar.

We already know $DU = \frac{s}{2}$ , so let's try to find it's analogous side for $\triangle TDV$ and $\triangle KFU$ . These sides are $DV$ and $FU$ , respectively.

First, $\frac{s}{2} = OD \cdot cos(54^{\circ})$ , so $OD = \frac{s}{2} \cdot sec(54^{\circ})$ . Then notice that $DV = \frac{OD}{2}$ because we have to fold $D$ to hit $O$ , so the folding crease has to be exactly halfway between $O$ and $D$ . Therefore, $DV = \frac{s}{4} \cdot sec(54^{\circ}) \implies \frac{DU}{DV} = \frac{\frac{s}{2}}{\frac{s}{4} \cdot sec(54^{\circ})} = 2 \cdot cos(54^{\circ})$

Now the ratio between the area of two similar triangles is the square of the ratio of their analogous side lengths. Thus $\frac{[ODU]}{[TDV]} = 4 \cdot cos^2(54^{\circ}) \implies \frac{10 \cdot [ODU]}{10 \cdot [TDV]} = 4 \cdot cos^2(54^{\circ})$ $\implies \frac{[ABCDE]}{10 \cdot [TDV]} = 4 \cdot cos^2(54^{\circ}) \implies \frac{\sqrt{5}+1}{10 \cdot [TDV]} = 4 \cdot cos^2(54^{\circ})$ $\implies 10 \cdot [TDV] = \frac{\sqrt{5}+1}{4 \cdot cos^2(54^{\circ})} \implies 10 \cdot [TDV] = \frac{\sqrt{5}+1}{4} \cdot sec^2(54^{\circ})$

Now let's move on and calculate the ratio of the other side length. Calculating $FU$ is slightly tricker. First, we find $TD$ : $TD \cdot cos(54^{\circ}) = DV = \frac{s}{4} sec^54^{\circ}) \implies TD = \frac{s}{4} \cdot sec^2(54^{\circ})$ . Now since $\triangle DTK$ is isosceles, $TD = DK$ and $UK = DK-DU = TD-DU = \frac{s}{4} \cdot sec^2(54^{\circ})-\frac{s}{2} = \frac{s}{4} \cdot (sec^2(54^{\circ})-2) = \frac{s}{4} \cdot (tan^2(54^{\circ})-1)$ .

Now $FU = UK \cdot tan(36^{\circ}) \implies FU \frac{s}{4} \cdot (tan^2(54^{\circ})-1) \cdot tan(36^{\circ})$ . Now note that $tan(x) \cdot tan(90-x) = 1$ because opposite over adjacent cancel each other out in a right triangle. Thus, $FU = \frac{s}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))$

Now, $\frac{DU}{FU} = \frac{\frac{s}{2}}{\frac{s}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))} = \frac{2}{tan(54^{\circ})-tan(36^{\circ})}$

$\implies \frac{[DU]}{[FU]} = \frac{4}{(tan(54^{\circ})-tan(36^{\circ}))^2} \implies 10 \cdot [FU] = \frac{1+\sqrt{5}}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))^2$

Now we go back to our first equation and plug in our values:

$[FGHIJ] = [ABCDE]-(10 \cdot [DVT]-10 \cdot [UFK]) \implies [FGHIJ] = 1+\sqrt{5}-\frac{\sqrt{5}+1}{4} \cdot sec^2(54^{\circ})+\frac{1+\sqrt{5}}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))^2$

$\implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (4-sec^2(54^{\circ})+(tan(54^{\circ})-tan(36^{\circ}))^2)$

Note $(tan(x)-tan(90-x))^2 = tan^2(x)-2 \cdot tan(x) \cdot tan(90-x)+tan^2(90-x) = tan^2(x)-2+tan^2(90-x)$ .

Also note that $tan^2(x)+1 = sec^2(x)$ . Thus $[FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (2-sec^2(54^{\circ})+tan^2(54^{\circ})+tan^2(36^{\circ}))$ $\implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (2+(-1)+tan^2(36^{\circ})) \implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (1+tan^2(36^{\circ}))$ .

Now all that remains is to find $tan^2(36^{\circ})$ . We can use the tan addition formula to find the general form of $tan(5x)$ or remember question 25 from this year's AMC 12A. We have that $tan(5x) = \frac{5tan(x)-10tan^3(x)+tan^5(x)}{1-10tan^2(x)+5tan^4(x)}$ .

Plug in $x=36$ . Then we have $tan(180^{\circ}) = \frac{5tan(36^{\circ})-10tan^3(36^{\circ})+tan^5(36^{\circ})}{1-10tan^2(36^{\circ})+5tan^4(36^{\circ})}$ Now let $y = tan(36^{\circ})$ . We have the equation $\frac{5y-10y^3+y^5}{1-10y^2+5y^4} = 0 \implies 5y-10y^3+y^5 = 0$ $\implies 5-10y^2+y^4 = 0 \implies 5-10z+z^2 = 0$ Where we let $z = y^2$ . Using the quadratic formula, we have $z = \frac{10 \pm \sqrt{80}}{2} = 5 \pm 2\sqrt{5}$ Now since $y = tan(36^{\circ})$ , $z = tan^2(36^{\circ})$ , which is what we were looking for. Notice that $tan(0^{\circ}) = 0$ and $tan(45^{\circ}) = 1$ , so $tan(36^{\circ})$ is between $0$ and $1$ , and so is it's square. Thus $z = 5 - 2\sqrt{5}$ , not the other root.

Finally:

$[FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (1+tan^2(36^{\circ})) = \frac{1+\sqrt{5}}{4} \cdot (1+5-2\sqrt{5})$ $\implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (6-2\sqrt{5}) = \frac{4\sqrt{5}-4}{4} = \sqrt{5}-1$

Therefore, $[FGHIJ] = \sqrt{5}-1 = \boxed{B}$

~KingRavi

Solution 3

$[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); // Draw the larger pentagon draw(A--B--C--D--E--cycle); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); draw(AA--OO, blue); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); draw(OOO--OAO,green); dot(O); dot((O+A)/2); label("$r_b$", (O+A)*.7, E,blue); label("$a_s$", (O+A)*.2 +(0+0.18,0.05), E,green); label("$r_s$", O+(-0.175,0.2), E,pink); label("$A$", (0,0), E); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); // Draw the smaller pentagon draw(F--G--H--I--J--cycle,red); draw(arc(O,(H+I)*.5*.6,H*.6)); label("$36^\circ$",O+(+0.05,0.15),NW); draw(O--H,pink); [/asy]$

Let $r_b$ and $r_s$ be the circumradius of the big and small pentagon, respectively. Let $a_s$ be the apothem of the smaller pentagon and $A_s$ and $A_b$ be the areas of the smaller and larger pentagon, respectively.

From the diagram: $\begin{align*} \cos{36^\circ} &= \dfrac{a_s}{r_s} = \dfrac{\phi}{2} = \dfrac{\sqrt{5}+1}{4}\\ a_s &= \dfrac{r_b}{2}\\ A_s &= \left(\dfrac{r_s}{r_b}\right)^2A_b\\ &=\left(\dfrac{a_s}{\cos{36^\circ} r_b}\right)^2 \left(1+\sqrt{5}\right)\\ &=\left(\dfrac{a_s}{\dfrac{\phi}{2} r_b}\right)^2 \left(1+\sqrt{5}\right)\\ &=\left(\dfrac{1}{2 \dfrac{\phi}{2}}\right)^2 \left(1+\sqrt{5}\right)\\ &=\left(\dfrac{2}{\sqrt{5}+1}\right)^2 \left(1+\sqrt{5}\right)\\ &=\dfrac{4}{\sqrt{5}+1} \\ &=\dfrac{4\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)} \\ &=\sqrt{5}-1 \end{align*}$ $\boxed{\textbf{(B) }\sqrt{5}-1}$ ~Technodoggo

Solution 4

Interestingly, we find that the pentagon we need is the one that is represented by the intersection of perpendicular bisectors of the connection from the center of the pentagon to one vertex. Through similar triangles and the golden ratio, we find that the side length ratio of the two pentagons is $\frac{\sqrt{5}-1}{2}$ Thus, the answer is $\sqrt{5}+1 \cdot (\frac{\sqrt{5}-1}{2})^2 = \sqrt{5}-1$ . $\boxed{\text{B}}$ ~andliu766

Solution 5 (answer choices (not rigorous))

After drawing a decent diagram, we can see that the area of the inner pentagon is quite a bit smaller than half the area of the larger pentagon.

Then, we can estimate the values of the answers and choose one that seems the closest to the smallest answer.

We know that $\sqrt5 \approx 2.236$ , so we'll use $\sqrt5=2.2$ for our estimations. The area of the original pentagon is $\sqrt5+1\approx3.2$ , so half of it is roughly $1.6$ .

A: $~4-\sqrt5\approx 1.8$ clearly, this is wrong because it is greater than half the area of the pentagon.

B: $\sqrt{5}-1 \approx 1.2$ This answer could be right.

C: $8-3\sqrt{5} \approx 1.4$ This too.

D: $\frac{\sqrt{5}+1}{2}$ This answer is wrong, as it assumes that the area of the inner pentagon is exactly half the area of the larger one.

E: $\frac{2+\sqrt{5}}{3}\approx1.4$ This answer could be right.

But, from our diagram, assume that the area of the pentagon is significantly less than the area half of the larger pentagon, so we choose the smallest answer choice, giving us $\boxed{\textbf{(B) }\sqrt{5}-1}$ . ~erics118

Supplement (Calculating sin54/cos36 from Scratch)

Method 1:

Construct golden ratio triangle $\triangle ABC$ with $\angle A = 36^{\circ}$ , $\angle B = \angle C = 72^{\circ}$ and $\triangle BCD$ with $\angle C = 36^{\circ}$ , $\angle DBC = \angle BDC = 72^{\circ}$ . WLOG, let $AB = AC = 1$ , $BC = CD = AD = a$ , $BD = 1-a$ . $\triangle BAC \sim \triangle BCD$

$\frac{AC}{BC} = \frac{BC}{BD}, \quad \frac{1}{a} = \frac{a}{1-a}, \quad 1-a=a^2, \quad a^2 + a - 1 = 0$

$a = \frac{ -1 + \sqrt{1^2 - 4(-1) } }{2} = \frac{ \sqrt{5} -1 }{2}$

$\cos 36^{\circ} = \cos \angle A = \frac{AE}{AC} = \frac{ 1-a }{2} + a = \frac{ a + 1 }{2} = \frac{ \frac{ \sqrt{5} -1 }{2} + 1 }{2} = \frac{ \sqrt{5} + 1 }{4}$

$\sin 54^{\circ} = \cos 36^{\circ} = \frac{ \sqrt{5} + 1 }{4}$

Method 2:

As explained here, $\cos \frac{2 \pi}{5} + \cos \frac{4 \pi}{5} = - \frac12$

$\cos \frac{2 \pi}{5} - \cos \frac{\pi}{5} = - \frac12$

$2(\cos\frac{ \pi}{5})^2 - 1 - \cos \frac{\pi}{5} = -1/2$

$4(\cos \frac{\pi}{5})^2 - 2 \cos \frac{\pi}{5} - 1 = 0$

$\cos 36^{\circ} = \cos \frac{\pi}{5} = \frac{2 + \sqrt{2^2 + 4 \cdot 4} }{8} = \frac{1+\sqrt{5}}{4}$

~isabelchen

Video Solution 1 by SpreadTheMathLove

https://www.youtube.com/watch?v=ROVjN3oYLbQ

Video Solution 2 by OmegaLearn

https://youtu.be/_WztOIk_2Q8

Video Solution

https://youtu.be/dGGPT9LYKxs

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

2023 AMC 10B (Problems • Answer Key • Resources)
Preceded by Problem 24	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 24	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search