Trigonometry
Trigonometry is the study of relations between the side lengths and angles of triangles through the trigonometric functions. It is a fundamental branch of mathematics, and its discovery paved the way towards countless famous results.
In contest math, trigonometry is an integral subfield of both geometry and algebra. Many essential results in geometry are written in terms of the trigonometric functions, such as the Law of Sines and the Law of Cosines; many more, such as Stewart's Theorem, are most easily proven using trigonometry. In algebra, expressions involving the trigonometric functions appear frequently on contests. These are solved by clever usage of the trigonometric functions' countless identities, which can simplify otherwise unwieldy equations.
Outside of competition math, trigonometry is the backbone of much of analysis. In particular, Fourier Analysis is written almost entirely in the language of the trigonometric functions.
Contents
[hide]Definitions
The trigonometric functions can be defined in several equivalent ways. The definition usually taught first is the right triangle definition, for its ease of access. An intermediate to olympiad geometry course usually uses the unit circle definition of trigonometry. Beyond the scope of contest math, the Taylor series definition of trigonometry is preferred in order to extend trigonometry to a complex domain.
Right triangle definition
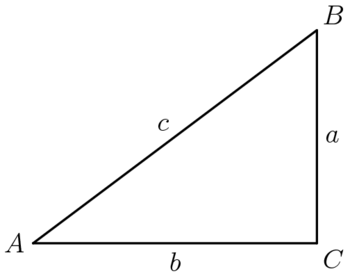
The right triangle definition of trigonometry involves the ratios between edges of a right triangle, with respect to a given angle. The definitions below will be referring to angle ![]() , with side lengths specified in the diagram. Because angle
, with side lengths specified in the diagram. Because angle ![]() must be less than
must be less than ![]() for the triangle to stay right, these definitions only work for acute angles.
for the triangle to stay right, these definitions only work for acute angles.
- Sine: The sine of angle
 , denoted
, denoted  , is defined as the ratio of the side opposite
, is defined as the ratio of the side opposite  to the hypotenuse.
to the hypotenuse. ![\[\sin (A) = \frac{\textrm{opposite}}{\textrm{hypotenuse}} = \frac{a}{c}.\]](//latex.artofproblemsolving.com/d/5/1/d51e2595afd41ed1215c94b583995eb3a8a64ce9.png)
- Cosine: The cosine of angle
 , denoted
, denoted  , is defined as the ratio of the side adjacent
, is defined as the ratio of the side adjacent  to the hypotenuse.
to the hypotenuse. ![\[\cos (A) = \frac{\textrm{adjacent}}{\textrm{hypotenuse}} = \frac{b}{c}.\]](//latex.artofproblemsolving.com/0/2/f/02f541010fd15cff8b523abb6d34671297b1a84e.png)
- Tangent: The tangent of angle
 , denoted
, denoted  , is defined as the ratio of the side opposite
, is defined as the ratio of the side opposite  to the side adjacent to
to the side adjacent to  .
. ![\[\tan (A) = \frac{\textrm{opposite}}{\textrm{adjacent}} = \frac{a}{b}.\]](//latex.artofproblemsolving.com/0/8/8/0888d2ff5bf0883f98414b16fc23db4cc9d4afd3.png)
A common mnemonic to remember this is SOH-CAH-TOA, where Sine = Opposite / Hypotenuse, Cosine = Adjacent / Hypotenuse, and Tangent = Opposite / Adjacent
More uncommon are the reciprocals of the trigonometric functions, listed below.
- Cosecant: The cosecant of angle
 , denoted
, denoted  , is defined as the reciprocal of the sine of
, is defined as the reciprocal of the sine of  .
. ![\[\csc (A) = \frac{1}{\sin (x)} = \frac{\textrm{hypotenuse}}{\textrm{opposite}} = \frac{c}{a}.\]](//latex.artofproblemsolving.com/6/e/8/6e85922c401a089d47d99982a02ad3043b772d45.png)
- Secant: The secant of angle
 , denoted
, denoted  , is defined as the reciprocal of the cosine of
, is defined as the reciprocal of the cosine of  .
. ![\[\sec (A) = \frac{1}{\cos (x)} = \frac{\textrm{hypotenuse}}{\textrm{adjacent}} = \frac{c}{b}.\]](//latex.artofproblemsolving.com/1/f/1/1f1760b80f18ba4905e623ad69a3126618a8f7e3.png)
- Cotangent: The cotangent of angle
 , denoted
, denoted  , is defined as the reciprocal of the tangent of
, is defined as the reciprocal of the tangent of  .
. ![\[\cot (A) = \frac{1}{\tan (x)} = \frac{\textrm{adjacent}}{\textrm{opposite}} = \frac{b}{a}.\]](//latex.artofproblemsolving.com/9/5/e/95e4a8e2ca2ac416da133b5ffe8a5be32117dd28.png)
The right triangle definition is most commonly taught in introductory geometry classes for its simplicity. However, it has its limitations. It only works if ![]() is right, which means that the trigonometric functions are only defined when angle
is right, which means that the trigonometric functions are only defined when angle ![]() is acute.
is acute.
Even though it is defined using right triangles, trigonometry is just as useful when used on acute and obtuse triangles. The Law of Sines and Law of Cosines mentioned below generalize the right triangle definition to include all triangles.
Unit circle definition
Consider the unit circle, the circle with radius one centered at the origin. Starting at ![]() , walk a distance
, walk a distance ![]() counterclockwise around the unit circle, as shown in the diagram. The coordinates of this point are defined to be
counterclockwise around the unit circle, as shown in the diagram. The coordinates of this point are defined to be ![]() .
.
As for the other trigonometric functions, ![]() is defined to be the ratio of
is defined to be the ratio of ![]() to
to ![]() , and cosecant, secant, and cotangent are defined to be the reciprocals of sine, cosine, and tangent, respectively.
, and cosecant, secant, and cotangent are defined to be the reciprocals of sine, cosine, and tangent, respectively.
The benefit of this definition is that it matches the right triangle definition for acute angles, but extends their domain from acute angles to all real-valued angles. As such, this definition is usually preferred in intermediate to olympiad geometry settings.
Taylor series definition
The Taylor series for sine and cosine are used as the definition of sine and cosine in analysis, particularly complex analysis. Defining the trigonometric functions this way gives a concrete way to extend the definition of trigonometry from the real numbers to the full complex plane. The taylor series for sine and cosine are shown below: ![]()
![]() These definitions are not used in high school math competitions; however, they do appear on the Putnam and other university competitions.
These definitions are not used in high school math competitions; however, they do appear on the Putnam and other university competitions.
Applications in Geometry
While trigonometry is useful at any level, intermediate competitions are particularly fond of geometric trigonometry questions. In addition to those mentioned
Law of Sines
The Law of Sines states that in any ![]() ,
, ![]() where
where ![]() is the side opposite to
is the side opposite to ![]() ,
, ![]() opposite to
opposite to ![]() ,
, ![]() opposite to
opposite to ![]() , and
, and ![]() is the circumradius of
is the circumradius of ![]() . The law of sines is particularly handy in problems involving the circumradius, seeing extremely wide usage in intermediate geometry.
. The law of sines is particularly handy in problems involving the circumradius, seeing extremely wide usage in intermediate geometry.
Law of cosines
The Law of Cosines states that in any ![]() ,
, ![]() where
where ![]() is the side opposite to
is the side opposite to ![]() ,
, ![]() opposite to
opposite to ![]() , and
, and ![]() opposite to
opposite to ![]() . It is a generalization of the Pythagorean Theorem and is used to prove several famous results, such as Heron's Formula and Stewart's Theorem. However, it sees limited applicability compared to the Law of Sines, as usage of the Law of Cosines can get algebra-heavy. It is helpful to memorize common, "nicer" values of sine and cosine as it can come in handy in contests, especially if you wish to apply either this or the Law of Sines to problems.
. It is a generalization of the Pythagorean Theorem and is used to prove several famous results, such as Heron's Formula and Stewart's Theorem. However, it sees limited applicability compared to the Law of Sines, as usage of the Law of Cosines can get algebra-heavy. It is helpful to memorize common, "nicer" values of sine and cosine as it can come in handy in contests, especially if you wish to apply either this or the Law of Sines to problems.
Trigonometric identities
Trigonometric identities are expressions true for all inputs involving the trigonometric functions. Due to the natural relationship between their definitions, these identities run numerous. In contest math, the most useful of these are:
- Pythagorean identities
- Angle addition identities
- Double angle identities
- Half angle identities
- Sum-to-product identities
- Product-to-sum identities