Unit circle
A unit circle is a circle whose radius has length 1.
In the Cartesian coordinate system, an equation of the form ![]() defines a unit circle with center
defines a unit circle with center ![]() .
.
Trigonometry
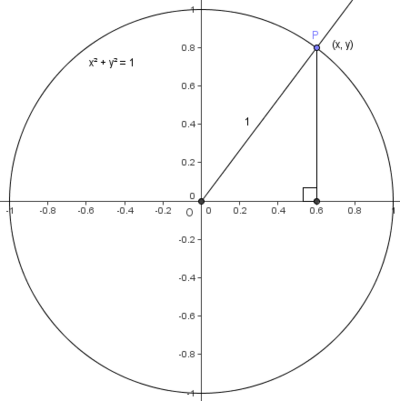
An unit circle centered at the origin can be used to calculate values for the basic trigonometric functions. Suppose we draw a ray starting from the origin and meeting the positive x-axis with an angle of ![]() . If we drop a perpendicular from the point of intersection between the ray and the circle, we have a right triangle with hypotenuse of
. If we drop a perpendicular from the point of intersection between the ray and the circle, we have a right triangle with hypotenuse of ![]() .
.
Using the definitions ![]() and
and ![]() , we find that
, we find that ![]() and
and ![]() .
.
We can read off values for sine and cosine of an angle this way; we can draw the angle and approximate the x and y coordinates of the intersection.
We can also prove one of he fundamental theorems of trigonometry: ![]() . The proof is as follows:
. The proof is as follows:
We see that the length and width of the triangle in the diagram at left are ![]() and
and ![]() , respectively. We use the pythagorean theorem to get:
, respectively. We use the pythagorean theorem to get:
![]()
Complex numbers
On the complex plane, all solutions to the polynomial ![]() lie upon the unit circle. These are referred to as the roots of unity.
lie upon the unit circle. These are referred to as the roots of unity.
In polar form, the solution to this polynomial can be expressed as ![]() , where
, where ![]() . This is commonly written as
. This is commonly written as ![]() . Additionally, the solution points form a regular
. Additionally, the solution points form a regular ![]() -gon on the unit circle.
-gon on the unit circle.
This article is a stub. Help us out by expanding it.