2024 AMC 10A Problems/Problem 22
Contents
Problem
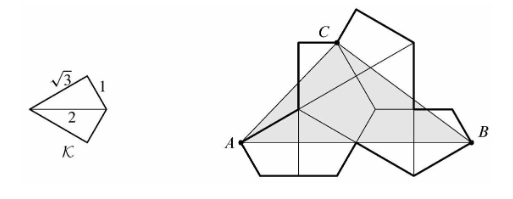
Let ![]() be the kite formed by joining two right triangles with legs
be the kite formed by joining two right triangles with legs ![]() and
and ![]() along a common hypotenuse. Eight copies of
along a common hypotenuse. Eight copies of ![]() are used to form the polygon shown below. What is the area of triangle
are used to form the polygon shown below. What is the area of triangle ![]() ?
?
![]()
Solution 3
 (latexing a WIP)
~mathboy282
~Thesmartgreekmathdude
(latexing a WIP)
~mathboy282
~Thesmartgreekmathdude
Solution 4
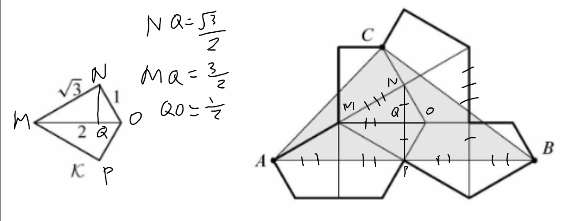
Let the point of intersection of ![]() and the kite with
and the kite with ![]() as vertex be
as vertex be ![]() .
.
Let the left kite with ![]() as a vertex touch the kite with
as a vertex touch the kite with ![]() as vertex at point
as vertex at point ![]() .
.
![]() is a
is a ![]() so
so ![]() and
and ![]() .
.
So, ![]() and
and ![]() , and the area is
, and the area is ![]()
~Mintylemon66
Solution 1
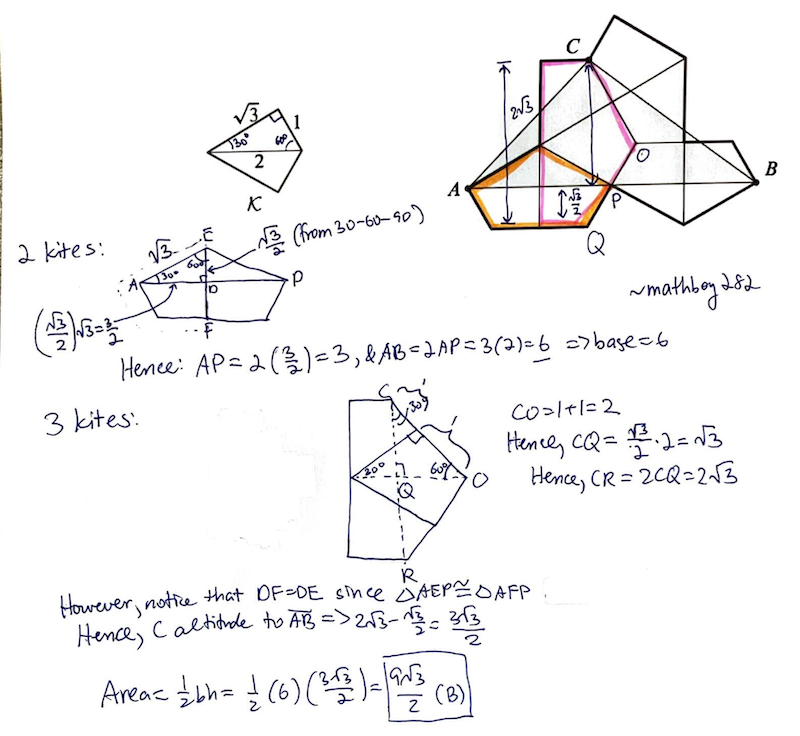
First, we should find the length of ![]() . In order to do this, as we see in the diagram, it can be split into 4 sections. Since diagram
. In order to do this, as we see in the diagram, it can be split into 4 sections. Since diagram ![]() shows us that it is made up of two
shows us that it is made up of two ![]() triangles, then the triangle outlined in red must be a
triangles, then the triangle outlined in red must be a ![]() triangle. Also, since we know the length of the longest side is
triangle. Also, since we know the length of the longest side is ![]() , then the side we are looking for, which is outlined in blue, must be
, then the side we are looking for, which is outlined in blue, must be ![]() by the
by the ![]() relationship of
relationship of ![]() triangles. Therefore the long side that is the base of the triangle we are looking for must be {6}.
triangles. Therefore the long side that is the base of the triangle we are looking for must be {6}.
Now all we have to do is find the height. We can split the height into 2 sections, the green and the light green. The green section must be ![]() , as
, as ![]() shows us. Also, the light green section must be equal to
shows us. Also, the light green section must be equal to ![]() , as in the previous paragraph, the triangle outlined in red is
, as in the previous paragraph, the triangle outlined in red is ![]() . Then, the green section, which is the height, must be
. Then, the green section, which is the height, must be ![]() , which is just
, which is just ![]() .
.
Then the area of the triangle must be ![]() , which is just
, which is just ![]()
~Solution by HappySharks
Solution 2
Let ![]() be quadrilateral
be quadrilateral ![]() . Drawing line
. Drawing line ![]() splits the triangle into
splits the triangle into ![]() .
Drawing the altitude from
.
Drawing the altitude from ![]() to point
to point ![]() on line
on line ![]() , we know
, we know ![]() is
is ![]() ,
, ![]() is
is ![]() , and
, and ![]() is
is ![]() .
.
Due to the many similarities present, we can find that ![]() is
is ![]() , and the height of
, and the height of ![]() is
is ![]()
![]() is
is ![]() and the height of
and the height of ![]() is
is ![]() .
.
Solving for the area of ![]() gives
gives ![]() which is
which is ![]()
~9897 (latex beginner here)
~i_am_suk_at_math(very minor latex edits)
Video Solution by Innovative Minds
https://www.youtube.com/watch?v=bhC58BB3kJA
~i_am_suk_at_math_2
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.