Difference between revisions of "1963 AHSME Problems/Problem 27"
Rockmanex3 (talk | contribs) (Solution to Problem 27) |
Omicrongamma (talk | contribs) m (→Solution 3) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 15: | Line 15: | ||
The first line divides the plane into two regions. The second line intersects one line, creating two regions. The third line intersects two lines, creating three regions. Similarly, the fourth line intersects three lines and creates four regions, the fifth line intersects four lines and creates five regions, and the sixth line intersects five lines and creates six regions. | The first line divides the plane into two regions. The second line intersects one line, creating two regions. The third line intersects two lines, creating three regions. Similarly, the fourth line intersects three lines and creates four regions, the fifth line intersects four lines and creates five regions, and the sixth line intersects five lines and creates six regions. | ||
| − | Totaling the regions created results in <math>2 + 2 + 3 + 4 + 5 + 6 = 22</math> regions, which is answer choice <math>\boxed{(C)}</math>. | + | Totaling the regions created results in <math>2 + 2 + 3 + 4 + 5 + 6 = 22</math> regions, which is answer choice <math>\boxed{\textbf{(C)}}</math>. |
===Solution 2=== | ===Solution 2=== | ||
| Line 21: | Line 21: | ||
[[Image:1963 AHSME Problem 27.png|300px|upright]] | [[Image:1963 AHSME Problem 27.png|300px|upright]] | ||
| − | With careful drawing, one can draw all six lines and count the regions. There are <math>22</math> regions in total, which is answer choice <math>\boxed{(C)}</math>. | + | With careful drawing, one can draw all six lines and count the regions. There are <math>22</math> regions in total, which is answer choice <math>\boxed{\textbf{(C)}}</math>. |
| + | |||
| + | ===Solution 3 === | ||
| + | |||
| + | We can use the fact that the number of regions that <math>n</math> lines divide a plane is given by the equation <math>L_n = \frac{n^2 + n +2}{2}</math>, and in this problems, <math>n=6</math>, from which the answer is <math>\boxed{22}</math>. | ||
| + | |||
| + | The formula is proved in Engel's Extremal Principles chapter or https://www.cut-the-knot.org/proofs/LinesDividePlane.shtml gives two proofs for it. | ||
| + | |||
| + | (OmicronGamma 2019) | ||
==See Also== | ==See Also== | ||
Latest revision as of 18:57, 13 January 2019
Problem
Six straight lines are drawn in a plane with no two parallel and no three concurrent. The number of regions into which they divide the plane is:
![]()
Solutions
Solution 1
The first line divides the plane into two regions. The second line intersects one line, creating two regions. The third line intersects two lines, creating three regions. Similarly, the fourth line intersects three lines and creates four regions, the fifth line intersects four lines and creates five regions, and the sixth line intersects five lines and creates six regions.
Totaling the regions created results in ![]() regions, which is answer choice
regions, which is answer choice ![]() .
.
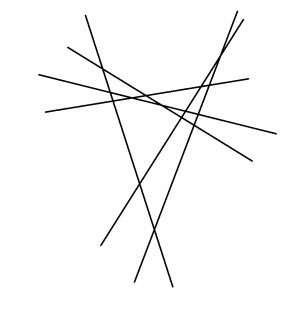
Solution 2
With careful drawing, one can draw all six lines and count the regions. There are ![]() regions in total, which is answer choice
regions in total, which is answer choice ![]() .
.
Solution 3
We can use the fact that the number of regions that ![]() lines divide a plane is given by the equation
lines divide a plane is given by the equation ![]() , and in this problems,
, and in this problems, ![]() , from which the answer is
, from which the answer is ![]() .
.
The formula is proved in Engel's Extremal Principles chapter or https://www.cut-the-knot.org/proofs/LinesDividePlane.shtml gives two proofs for it.
(OmicronGamma 2019)
See Also
| 1963 AHSC (Problems • Answer Key • Resources) | ||
| Preceded by Problem 26 |
Followed by Problem 28 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 • 31 • 32 • 33 • 34 • 35 • 36 • 37 • 38 • 39 • 40 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()