Difference between revisions of "2003 AMC 12A Problems"
m |
m (→Problem 25) |
||
| Line 144: | Line 144: | ||
== Problem 25 == | == Problem 25 == | ||
| + | Let <math>\displaystyle f(x)= \sqrt{ax^2+bx} </math>. For how many real values of <math>a</math> is there at least one positive value of <math> b </math> for which the domain of <math>f </math> and the range <math> f </math> are the same set? | ||
| + | |||
| + | <math> \mathrm{(A) \ 0 } \qquad \mathrm{(B) \ 1 } \qquad \mathrm{(C) \ 2 } \qquad \mathrm{(D) \ 3 } \qquad \mathrm{(E) \ \mathrm{infinitely \ many} } </math> | ||
[[2003 AMC 12A Problems/Problem 25|Solution]] | [[2003 AMC 12A Problems/Problem 25|Solution]] | ||
Revision as of 16:30, 28 November 2006
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
What is the difference between the sum of the first ![]() even counting numbers and the sum of the first
even counting numbers and the sum of the first ![]() odd counting numbers?
odd counting numbers?
![]()
Problem 2
Members of the Rockham Soccer Leauge buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the Leauge?
![]()
Problem 3
A solid box is ![]() cm by
cm by ![]() cm by
cm by ![]() cm. A new solid is formed by removing a cube
cm. A new solid is formed by removing a cube ![]() cm on a side from each corner of this box. What percent of the original volume is removed?
cm on a side from each corner of this box. What percent of the original volume is removed?
![]()
Problem 4
It takes Mary ![]() minutes to walk uphill
minutes to walk uphill ![]() km from her home to school, but it takes her only
km from her home to school, but it takes her only ![]() minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?
minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?
![]()
Problem 5
The sum of the two 5-digit numbers ![]() and
and ![]() is
is ![]() . What is
. What is ![]() ?
?
![]()
Problem 6
Define ![]() to be
to be ![]() for all real numbers
for all real numbers ![]() and
and ![]() . Which of the following statements is not true?
. Which of the following statements is not true?
![]() for all
for all ![]() and
and ![]()
![]() for all
for all ![]() and
and ![]()
![]() for all
for all ![]()
![]() for all
for all ![]()
![]() if
if ![]()
Problem 7
How many non-congruent triangles with perimeter ![]() have integer side lengths?
have integer side lengths?
![]()
Problem 8
What is the probability that a randomly drawn positive factor of ![]() is less than
is less than ![]()
![]()
Problem 9
Problem 10
Problem 11
Problem 12
Sally has five red cards numbered ![]() through
through ![]() and four blue cards numbered
and four blue cards numbered ![]() through
through ![]() . She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?
. She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?
![]()
Problem 13
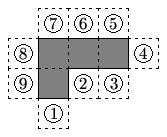
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attatched to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?
![]()
Problem 14
Problem 15
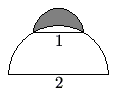
A semicircle of diameter ![]() sits at the top of a semicircle of diameter
sits at the top of a semicircle of diameter ![]() , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
, as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
![]()
Problem 16
Problem 17
Problem 18
Let ![]() be a
be a ![]() -digit number, and let
-digit number, and let ![]() and
and ![]() be the quotient and the remainder, respectively, when
be the quotient and the remainder, respectively, when ![]() is divided by
is divided by ![]() . For how many values of
. For how many values of ![]() is
is ![]() divisible by
divisible by ![]() ?
?
![]()
Problem 19
Problem 20
Problem 21
Problem 22
Problem 23
Problem 24
Problem 25
Let ![]() . For how many real values of
. For how many real values of ![]() is there at least one positive value of
is there at least one positive value of ![]() for which the domain of
for which the domain of ![]() and the range
and the range ![]() are the same set?
are the same set?
![]()