Difference between revisions of "2013 AIME I Problems/Problem 13"
Hashtagmath (talk | contribs) |
Fuzimiao2013 (talk | contribs) m (→Solution 1 (Simple, Sane Solution)) |
||
| Line 7: | Line 7: | ||
For ease, all ratios I will use to solve this problem are with respect to the area of <math>AB_0C_0</math>. For example, if I say some area has ratio <math>\frac{1}{2}</math>, that means its area is 45. | For ease, all ratios I will use to solve this problem are with respect to the area of <math>AB_0C_0</math>. For example, if I say some area has ratio <math>\frac{1}{2}</math>, that means its area is 45. | ||
| − | Now note that <math>k=</math> 1 minus ratio of <math>B_1C_1A</math> minus ratio <math>B_0C_0C_1</math>. We see by similar triangles given that ratio <math>B_0C_0C_1</math> is <math>\frac{17^2}{25^2}</math>. Ratio <math>B_1C_1A</math> is, after seeing that <math>C_1C_0 = \frac{289}{625}</math>, <math>(\frac{336}{625})^2</math>. Now it suffices to find 90 times ratio <math>B_0B_1C_1</math>, which is given by 1 minus the two aforementioned ratios. Substituting these ratios to find <math>k</math> and clearing out the <math>5^8</math>, we see that the answer is <math>90\cdot \frac{5^8-336^2-17^2\cdot 5^4}{5^8-336^2}</math>. Calculation might take some time, but you've solved the problem! <math> | + | Now note that <math>k=</math> 1 minus ratio of <math>B_1C_1A</math> minus ratio <math>B_0C_0C_1</math>. We see by similar triangles given that ratio <math>B_0C_0C_1</math> is <math>\frac{17^2}{25^2}</math>. Ratio <math>B_1C_1A</math> is, after seeing that <math>C_1C_0 = \frac{289}{625}</math>, <math>(\frac{336}{625})^2</math>. Now it suffices to find 90 times ratio <math>B_0B_1C_1</math>, which is given by 1 minus the two aforementioned ratios. Substituting these ratios to find <math>k</math> and clearing out the <math>5^8</math>, we see that the answer is <math>90\cdot \frac{5^8-336^2-17^2\cdot 5^4}{5^8-336^2}</math>. Calculation might take some time, but you've solved the problem! <math>q= \boxed{961}</math>. |
== Solution 2 == | == Solution 2 == | ||
Revision as of 23:37, 1 March 2021
Problem
Triangle ![]() has side lengths
has side lengths ![]() ,
, ![]() , and
, and ![]() . For each positive integer
. For each positive integer ![]() , points
, points ![]() and
and ![]() are located on
are located on ![]() and
and ![]() , respectively, creating three similar triangles
, respectively, creating three similar triangles ![]() . The area of the union of all triangles
. The area of the union of all triangles ![]() for
for ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1 (Simple, Sane Solution)
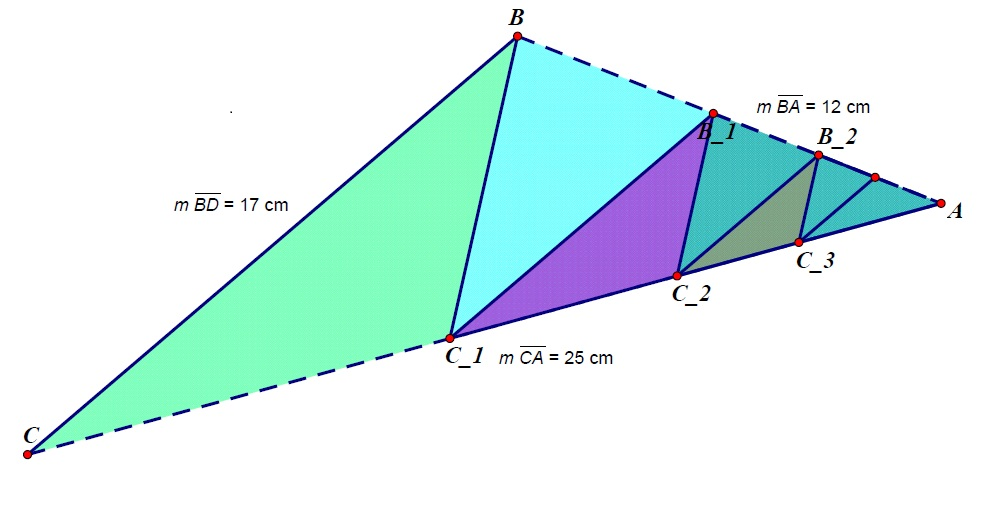
Well, first draw a good diagram! One is provided below. Convince yourself that every ![]() is parallel to each other for any nonnegative
is parallel to each other for any nonnegative ![]() . Next, convince yourself that the area we seek is simply the ratio
. Next, convince yourself that the area we seek is simply the ratio ![]() , because it repeats in smaller and smaller units. Note that the area of the triangle, by Heron's formula, is 90.
, because it repeats in smaller and smaller units. Note that the area of the triangle, by Heron's formula, is 90.
For ease, all ratios I will use to solve this problem are with respect to the area of ![]() . For example, if I say some area has ratio
. For example, if I say some area has ratio ![]() , that means its area is 45.
, that means its area is 45.
Now note that ![]() 1 minus ratio of
1 minus ratio of ![]() minus ratio
minus ratio ![]() . We see by similar triangles given that ratio
. We see by similar triangles given that ratio ![]() is
is ![]() . Ratio
. Ratio ![]() is, after seeing that
is, after seeing that ![]() ,
, ![]() . Now it suffices to find 90 times ratio
. Now it suffices to find 90 times ratio ![]() , which is given by 1 minus the two aforementioned ratios. Substituting these ratios to find
, which is given by 1 minus the two aforementioned ratios. Substituting these ratios to find ![]() and clearing out the
and clearing out the ![]() , we see that the answer is
, we see that the answer is ![]() . Calculation might take some time, but you've solved the problem!
. Calculation might take some time, but you've solved the problem! ![]() .
.
Solution 2
Using Heron's Formula we can get the area of the triangle ![]() .
.
Since ![]() then the scale factor for the dimensions of
then the scale factor for the dimensions of ![]() to
to ![]() is
is ![]()
Therefore, the area of ![]() is
is ![]() . Also, the dimensions of the other sides of the
. Also, the dimensions of the other sides of the ![]() can be
easily computed:
can be
easily computed: ![]() and
and ![]() . This allows us to compute one side of the
triangle
. This allows us to compute one side of the
triangle ![]() ,
, ![]() . Therefore, the scale factor
. Therefore, the scale factor ![]() to
to ![]() is
is ![]() , which yields the length of
, which yields the length of ![]() as
as ![]() .
Therefore, the scale factor for
.
Therefore, the scale factor for ![]() to
to ![]() is
is ![]() . Some more algebraic manipulation will show that
. Some more algebraic manipulation will show that ![]() to
to ![]() is still
is still ![]() . Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
. Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
![]() At this point, it may be wise to "simplify"
At this point, it may be wise to "simplify" ![]() .
So the geometric series converges to
.
So the geometric series converges to
 .
Using the difference of squares, we get
.
Using the difference of squares, we get ![]() , which simplifies to
, which simplifies to ![]() . Cancelling all common factors, we get the reduced fraction
. Cancelling all common factors, we get the reduced fraction ![]() . So
. So ![]() , yielding the answer
, yielding the answer ![]() .
.
See also
| 2013 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.