Difference between revisions of "2020 AMC 12A Problems/Problem 25"
MRENTHUSIASM (talk | contribs) (→Remarks of Solution 2 and Video Solution 3) |
MRENTHUSIASM (talk | contribs) m (→Remarks of Solution 2 and Video Solution 3: I moved the large contents of extensions to the Discussion Page. Now this page is much cleaner. I also direct the reader to the Discussion Page.) |
||
| Line 34: | Line 34: | ||
Created by Richard Rusczyk | Created by Richard Rusczyk | ||
| − | ==Remarks | + | ==Remarks== |
===Graph=== | ===Graph=== | ||
Let <math>f(x)=\lfloor x \rfloor \cdot \{x\}.</math> | Let <math>f(x)=\lfloor x \rfloor \cdot \{x\}.</math> | ||
| Line 59: | Line 59: | ||
~MRENTHUSIASM (Graph by Desmos: https://www.desmos.com/calculator/ouvaiqjdzj) | ~MRENTHUSIASM (Graph by Desmos: https://www.desmos.com/calculator/ouvaiqjdzj) | ||
| − | === | + | ===Extensions=== |
Visit the [https://artofproblemsolving.com/wiki/index.php/Talk:2020_AMC_12A_Problems/Problem_25 Discussion Page] for the underlying arguments and additional questions. | Visit the [https://artofproblemsolving.com/wiki/index.php/Talk:2020_AMC_12A_Problems/Problem_25 Discussion Page] for the underlying arguments and additional questions. | ||
Revision as of 01:14, 17 April 2021
Contents
[hide]Problem
The number ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers, has the property that the sum of all real numbers
are relatively prime positive integers, has the property that the sum of all real numbers ![]() satisfying
satisfying
![]() is
is ![]() , where
, where ![]() denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to ![]() and
and ![]() denotes the fractional part of
denotes the fractional part of ![]() . What is
. What is ![]() ?
?
![]()
Solution 1
Let ![]() be the unique solution in this range. Note that
be the unique solution in this range. Note that ![]() is also a solution as long as
is also a solution as long as ![]() , hence all our solutions are
, hence all our solutions are ![]() for some
for some ![]() . This sum
. This sum ![]() must be between
must be between ![]() and
and ![]() , which gives
, which gives ![]() and
and ![]() . Plugging this back in gives
. Plugging this back in gives ![]() .
.
Solution 2
First note that ![]() when
when ![]() while
while ![]() . Thus we only need to look at positive solutions (
. Thus we only need to look at positive solutions (![]() doesn't affect the sum of the solutions).
Next, we breakdown
doesn't affect the sum of the solutions).
Next, we breakdown ![]() down for each interval
down for each interval ![]() , where
, where ![]() is a positive integer. Assume
is a positive integer. Assume ![]() , then
, then ![]() . This means that when
. This means that when ![]() ,
, ![]() . Setting this equal to
. Setting this equal to ![]() gives
gives
![]() We're looking at the solution with the positive
We're looking at the solution with the positive ![]() , which is
, which is ![]() . Note that if
. Note that if ![]() is the greatest
is the greatest ![]() such that
such that ![]() has a solution, the sum of all these solutions is slightly over
has a solution, the sum of all these solutions is slightly over ![]() , which is
, which is ![]() when
when ![]() , just under
, just under ![]() . Checking this gives
. Checking this gives
![\[\sum_{k=1}^{28}\frac{k}{2a}\left(1-\sqrt{1-4a}\right)=\frac{1-\sqrt{1-4a}}{2a}\cdot 406=420\]](http://latex.artofproblemsolving.com/b/5/1/b5129586fdf11baae2fb73ec8869a64d5fc09866.png)
![]()
![]()
![]()
![]()
![]()
![]() ~ktong
~ktong
Video Solution 1 (Geometry)
This video shows how things like The Pythagorean Theorem and The Law of Sines work together to solve this seemingly algebraic problem: https://www.youtube.com/watch?v=6IJ7Jxa98zw&feature=youtu.be
Video Solution 2
https://www.youtube.com/watch?v=xex8TBSzKNE ~ MathEx
Video Solution 3 (by Art of Problem Solving)
https://www.youtube.com/watch?v=7_mdreGBPvg&t=428s&ab_channel=ArtofProblemSolving
Created by Richard Rusczyk
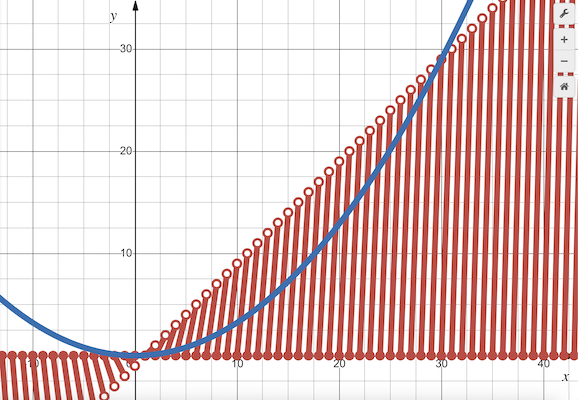
Remarks
Graph
Let ![]()
We make the following table of values:
![\[\begin{array}{c|c|c|clc} \boldsymbol{x} & \boldsymbol{\lfloor x \rfloor} & \boldsymbol{f(x)} & & \hspace{4mm}\textbf{Equation} & \\ [1.5ex] \hline & & & & & \\ [-1ex] [0,1) & 0 & 0 & & y=0 & \\ [1.5ex] [1,2) & 1 & [0,1) & & y=x-1 & \\ [1.5ex] [2,3) & 2 & [0,2) & & y=2x-4 & \\ [1.5ex] [3,4) & 3 & [0,3) & & y=3x-9 & \\ [1.5ex] [4,5) & 4 & [0,4) & & y=4x-16 & \\ [1.5ex] \cdots & \cdots & \cdots & & \ \ \ \ \ \ \ \cdots & \\ [1.5ex] [m,m+1) & m & [0,m) & & y=mx-m^2 & \end{array}\]](http://latex.artofproblemsolving.com/1/f/1/1f16a70b133880e1b2dbcdfcff698bb3db19c627.png)
We graph ![]() by branches:
by branches:
~MRENTHUSIASM (Graph by Desmos: https://www.desmos.com/calculator/ouvaiqjdzj)
Extensions
Visit the Discussion Page for the underlying arguments and additional questions.
~MRENTHUSIASM
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()