Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AMC 8 Problems/Problem 25"

m (→‎Solution 2 (Recursion))
m (→‎Solution 2 (Recursion))
Line 30: Line 30:
 
==Solution 2 (Recursion)==
 
==Solution 2 (Recursion)==
  
−
Denote <math>P_n</math> to be the probability that the cricket would return back to the first point after <math>n</math> hops. Then, we get the recursive formula <math>P_n = \frac13(1-P_{n-1})</math> because if the leaf is not on the target leaf, then there is a <math>\frac13</math> probability that he’ll make it back. With this formula and the fact that <math>P_0=0,</math> we have <cmath>P_1 = \frac13, P_2 = \frac29, P_3 = \frac7{27},</cmath> so our answer is <math>\boxed{\textbf{(E) }\frac{7}{27}}</math>.
+
Denote <math>P_n</math> to be the probability that the cricket would return back to the first point after <math>n</math> hops. Then, we get the recursive formula <cmath>P_n = \frac13(1-P_{n-1})</cmath> because if the leaf is not on the target leaf, then there is a <math>\frac13</math> probability that it will make it back. With this formula and the fact that <math>P_0=0,</math> we have <cmath>P_1 = \frac13, P_2 = \frac29, P_3 = \frac7{27},</cmath> so our answer is <math>\boxed{\textbf{(E) }\frac{7}{27}}</math>.
  
 
~wamofan
 
~wamofan

Revision as of 20:14, 28 January 2022

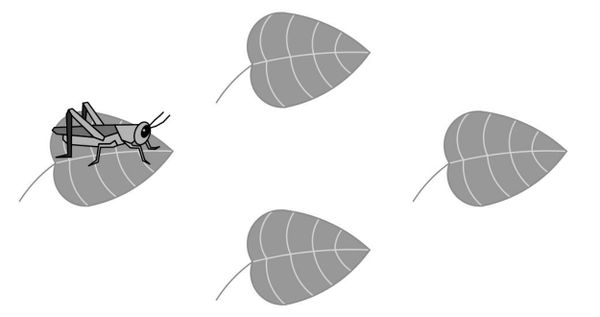
Problem

A cricket randomly hops between $4$ leaves, on each turn hopping to one of the other $3$ leaves with equal probability. After $4$ hops what is the probability that the cricket has returned to the leaf where it started?

2022 AMC 8 Problem 25 Picture.jpg

$\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}$

Solution 1 (Casework)

Let $A$ denote the leaf where the cricket starts and $B$ denote one of the other $3$ leaves. Note that:

  • If the cricket is at $A,$ then the probability that it hops to $B$ next is $1.$
  • If the cricket is at $B,$ then the probability that it hops to $A$ next is $\frac13.$
  • If the cricket is at $B,$ then the probability that it hops to $B$ next is $\frac23.$

We apply casework to the possible paths of the cricket:

  1. $A \longrightarrow B \longrightarrow A \longrightarrow B \longrightarrow A$

    The probability for this case is $1\cdot\frac13\cdot1\cdot\frac13=\frac19.$

  2. $A \longrightarrow B \longrightarrow B \longrightarrow B \longrightarrow A$

    The probability for this case is $1\cdot\frac23\cdot\frac23\cdot\frac13=\frac{4}{27}.$

Together, the probability that the cricket returns to $A$ is $\frac19+\frac{4}{27}=\boxed{\textbf{(E) }\frac{7}{27}}.$

~MRENTHUSIASM

Solution 2 (Recursion)

Denote $P_n$ to be the probability that the cricket would return back to the first point after $n$ hops. Then, we get the recursive formula \[P_n = \frac13(1-P_{n-1})\] because if the leaf is not on the target leaf, then there is a $\frac13$ probability that it will make it back. With this formula and the fact that $P_0=0,$ we have \[P_1 = \frac13, P_2 = \frac29, P_3 = \frac7{27},\] so our answer is $\boxed{\textbf{(E) }\frac{7}{27}}$.

~wamofan

See Also

2022 AMC 8 (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AMC_8_Problems/Problem_25&oldid=170629"