Difference between revisions of "2001 USAMO Problems/Problem 4"
Wwwrqnojcm (talk | contribs) m (→Solution 1) |
(→Solution) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 45: | Line 45: | ||
Therefore <math>P</math> cannot be inside or on the sides of triangle <math>ABC</math>. Since this covers all four cases, <math>ABPC</math> is convex. | Therefore <math>P</math> cannot be inside or on the sides of triangle <math>ABC</math>. Since this covers all four cases, <math>ABPC</math> is convex. | ||
| − | ==Solution 4== | + | ===Solution 4=== |
Let <math>P</math> be the origin in vector space, and let <math>a, b, c</math> denote the position vectors of <math>A, B, C</math> respectively. Then the obtuse triangle condition, <math>PA^2 > PB^2 + PC^2</math>, becomes <math>a^2 > b^2 + c^2</math> using the fact that the square of a vector (the dot product of itself and itself) is the square of its magnitude. Now, notice that to prove <math>\angle{BAC}</math> is acute, it suffices to show that <math>(a - b)(a - c) > 0</math>, or <math>a^2 - ab - ac + bc > 0</math>. But this follows from the observation that | Let <math>P</math> be the origin in vector space, and let <math>a, b, c</math> denote the position vectors of <math>A, B, C</math> respectively. Then the obtuse triangle condition, <math>PA^2 > PB^2 + PC^2</math>, becomes <math>a^2 > b^2 + c^2</math> using the fact that the square of a vector (the dot product of itself and itself) is the square of its magnitude. Now, notice that to prove <math>\angle{BAC}</math> is acute, it suffices to show that <math>(a - b)(a - c) > 0</math>, or <math>a^2 - ab - ac + bc > 0</math>. But this follows from the observation that | ||
<cmath>(-a + b + c)^2 \ge 0,</cmath> | <cmath>(-a + b + c)^2 \ge 0,</cmath> | ||
| Line 51: | Line 51: | ||
<cmath>2a^2 - 2ab - 2ac + 2bc > a^2 + b^2 + c^2 - 2ab - 2ac + 2bc \ge 0</cmath> | <cmath>2a^2 - 2ab - 2ac + 2bc > a^2 + b^2 + c^2 - 2ab - 2ac + 2bc \ge 0</cmath> | ||
and therefore our desired conclusion. | and therefore our desired conclusion. | ||
| + | |||
| + | ===Solution 5=== | ||
| + | Let <math>M, N</math> be midpoints of <math>AP</math> and <math>BC</math>, respectively. For the points <math>A, B, P, C</math>; let's apply Euler's quadrilateral formula, | ||
| + | <cmath> AB^2 + BP^2 + PC^2 + CA^2 = AP^2 + BC^2 + 4MN^2 \geq AP^2 + BC^2 .</cmath> | ||
| + | Given that <math>AP^2 > BP^2 + PC^2</math>. Thus, | ||
| + | <cmath> AB^2 + AC^2 > BC^2 .</cmath> | ||
| + | and we get <math>\angle BAC</math> is acute. | ||
| + | |||
| + | (Lokman GÖKÇE) | ||
| + | |||
| + | ===Solution 6=== | ||
| + | Without loss of generality, assume that in a Cartesian coordinate system, <math>A</math> is at the point <math>(0, 0)</math> and <math>C</math> is at the point <math>(1,0)</math>. Let <math>B</math> be at the point <math>(b_x,b_y)</math> and <math>P</math> be at the point <math>(p_x,p_y)</math>. Without loss of generality, also assume that <math>b_y>0</math>. | ||
| + | |||
| + | Now, assume for contradiction that <math>\angle BAC</math> is not acute. Since <math>PA</math>, <math>PB</math>, and <math>PC</math> are the sides of an obtuse triangle, with <math>PA</math> the longest side, it follows that <math>PA^2>PB^2+PC^2</math>, implying that <math>p_x^2+p_y^2>(p_x-b_x)^2+(p_y-b_y)^2+(p_x-1)^2+p_y^2</math>. This inequality simplifies to <math>b_x^2-2p_x b_x+b_y^2-2p_y b_y+p_x^2-2p_x+1+p_y^2<0</math>. Note that since <math>p_x^2-2p_x+1</math> and <math>b_y^2-2p_y b_y+p_y^2</math> are both perfect squares, all terms of this inequality except for <math>-2p_x b_x</math> are already guaranteed to be nonnegative. | ||
| + | |||
| + | If <math>p_x<0</math>, then <math>P</math> would be closer to <math>A</math> than to <math>C</math>, but since <math>PA^2=PB^2+PC^2</math>, this is not possible. Therefore, <math>p_x \geq 0</math>. Since <math>\angle BAC</math> not being acute implies that <math>b_x \leq 0</math>, it follows that <math>-2p_x b_x \geq 0</math>. But now since all terms of <math>b_x^2-2p_x b_x+b_y^2-2p_y b_y+p_x^2-2p_x+1+p_y^2<0</math> are guaranteed to be nonnegative, this entire expression cannot be negative, leading to a contradiction. Therefore, <math>\angle BAC</math> is acute. | ||
== See also == | == See also == | ||
Latest revision as of 21:24, 18 June 2022
Contents
[hide]Problem
Let ![]() be a point in the plane of triangle
be a point in the plane of triangle ![]() such that the segments
such that the segments ![]() ,
, ![]() , and
, and ![]() are the sides of an obtuse triangle. Assume that in this triangle the obtuse angle opposes the side congruent to
are the sides of an obtuse triangle. Assume that in this triangle the obtuse angle opposes the side congruent to ![]() . Prove that
. Prove that ![]() is acute.
is acute.
Solution
Solution 1
We know that ![]() and we wish to prove that
and we wish to prove that ![]() .
It would be sufficient to prove that
.
It would be sufficient to prove that
![]() Set
Set ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Then, we wish to show
.
Then, we wish to show
![]()
![]()
![]()
![]()
![]()
which is true by the trivial inequality.
Solution 2
Let ![]() be the origin. For a point
be the origin. For a point ![]() , denote by
, denote by ![]() the vector
the vector ![]() , and denote by
, and denote by ![]() the length of
the length of ![]() . The given conditions may be written as
. The given conditions may be written as
![]() or
or
![]() Adding
Adding ![]() on both sides of the last inequality gives
on both sides of the last inequality gives
![]() Since the left-hand side of the last inequality is nonnegative, the right-hand side is positive. Hence
Since the left-hand side of the last inequality is nonnegative, the right-hand side is positive. Hence
![]() that is,
that is, ![]() is acute.
is acute.
Solution 3
For the sake of contradiction, let's assume to the contrary that ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . Then
. Then ![]() . We claim that the quadrilateral
. We claim that the quadrilateral ![]() is convex. Now applying the generalized Ptolemy's Theorem to the convex quadrilateral
is convex. Now applying the generalized Ptolemy's Theorem to the convex quadrilateral ![]() yields
yields
![]() where the second inequality is by Cauchy-Schwarz. This implies
where the second inequality is by Cauchy-Schwarz. This implies ![]() , in contradiction with the facts that
, in contradiction with the facts that ![]() ,
, ![]() , and
, and ![]() are the sides of an obtuse triangle and
are the sides of an obtuse triangle and ![]() .
.
We present two arguments to prove our claim.
First argument: Without loss of generality, we may assume that ![]() ,
, ![]() , and
, and ![]() are in counterclockwise order. Let lines
are in counterclockwise order. Let lines ![]() and
and ![]() be the perpendicular bisectors of segments
be the perpendicular bisectors of segments ![]() and
and ![]() , respectively. Then
, respectively. Then ![]() and
and ![]() meet at
meet at ![]() , the circumcenter of triangle
, the circumcenter of triangle ![]() . Lines
. Lines ![]() and
and ![]() cut the plane into four regions and
cut the plane into four regions and ![]() is in the interior of one of these regions. Since
is in the interior of one of these regions. Since ![]() and
and ![]() ,
, ![]() must be in the interior of the region that opposes
must be in the interior of the region that opposes ![]() . Since
. Since ![]() is not acute, ray
is not acute, ray ![]() does not meet
does not meet ![]() and ray
and ray ![]() does not meet
does not meet ![]() . Hence
. Hence ![]() and
and ![]() must lie in the interiors of the regions adjacent to
must lie in the interiors of the regions adjacent to ![]() . Let
. Let ![]() denote the region containing
denote the region containing ![]() . Then
. Then ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are the four regions in counterclockwise order. Since
are the four regions in counterclockwise order. Since ![]() , either
, either ![]() is on side
is on side ![]() or
or ![]() and
and ![]() are on opposite sides of line
are on opposite sides of line ![]() . In either case
. In either case ![]() and
and ![]() are on opposite sides of line
are on opposite sides of line ![]() . Also, since ray
. Also, since ray ![]() does not meet
does not meet ![]() and ray
and ray ![]() does not meet
does not meet ![]() , it follows that
, it follows that ![]() is entirely in the interior of
is entirely in the interior of ![]() . Hence
. Hence ![]() and
and ![]() are on opposite sides of
are on opposite sides of ![]() . Therefore
. Therefore ![]() is convex.
is convex.
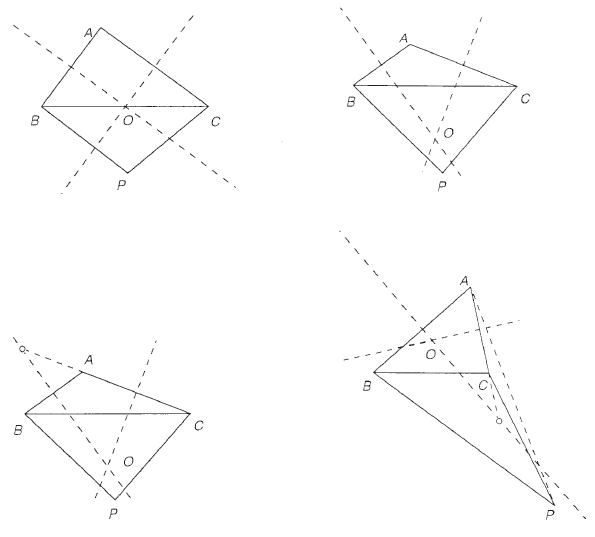
Second argument: Since ![]() and
and ![]() ,
, ![]() cannot be inside or on the sides of triangle
cannot be inside or on the sides of triangle ![]() . Since
. Since ![]() , we have
, we have ![]() and hence
and hence ![]() . Hence
. Hence ![]() cannot be inside or on the sides of triangle
cannot be inside or on the sides of triangle ![]() . Symmetrically,
. Symmetrically, ![]() cannot be inside or on the sides of triangle
cannot be inside or on the sides of triangle ![]() . Finally, since
. Finally, since ![]() and
and ![]() , we have
, we have
![]() Therefore
Therefore ![]() cannot be inside or on the sides of triangle
cannot be inside or on the sides of triangle ![]() . Since this covers all four cases,
. Since this covers all four cases, ![]() is convex.
is convex.
Solution 4
Let ![]() be the origin in vector space, and let
be the origin in vector space, and let ![]() denote the position vectors of
denote the position vectors of ![]() respectively. Then the obtuse triangle condition,
respectively. Then the obtuse triangle condition, ![]() , becomes
, becomes ![]() using the fact that the square of a vector (the dot product of itself and itself) is the square of its magnitude. Now, notice that to prove
using the fact that the square of a vector (the dot product of itself and itself) is the square of its magnitude. Now, notice that to prove ![]() is acute, it suffices to show that
is acute, it suffices to show that ![]() , or
, or ![]() . But this follows from the observation that
. But this follows from the observation that
![]() which leads to
which leads to
![]() and therefore our desired conclusion.
and therefore our desired conclusion.
Solution 5
Let ![]() be midpoints of
be midpoints of ![]() and
and ![]() , respectively. For the points
, respectively. For the points ![]() ; let's apply Euler's quadrilateral formula,
; let's apply Euler's quadrilateral formula,
![]() Given that
Given that ![]() . Thus,
. Thus,
![]() and we get
and we get ![]() is acute.
is acute.
(Lokman GÖKÇE)
Solution 6
Without loss of generality, assume that in a Cartesian coordinate system, ![]() is at the point
is at the point ![]() and
and ![]() is at the point
is at the point ![]() . Let
. Let ![]() be at the point
be at the point ![]() and
and ![]() be at the point
be at the point ![]() . Without loss of generality, also assume that
. Without loss of generality, also assume that ![]() .
.
Now, assume for contradiction that ![]() is not acute. Since
is not acute. Since ![]() ,
, ![]() , and
, and ![]() are the sides of an obtuse triangle, with
are the sides of an obtuse triangle, with ![]() the longest side, it follows that
the longest side, it follows that ![]() , implying that
, implying that ![]() . This inequality simplifies to
. This inequality simplifies to ![]() . Note that since
. Note that since ![]() and
and ![]() are both perfect squares, all terms of this inequality except for
are both perfect squares, all terms of this inequality except for ![]() are already guaranteed to be nonnegative.
are already guaranteed to be nonnegative.
If ![]() , then
, then ![]() would be closer to
would be closer to ![]() than to
than to ![]() , but since
, but since ![]() , this is not possible. Therefore,
, this is not possible. Therefore, ![]() . Since
. Since ![]() not being acute implies that
not being acute implies that ![]() , it follows that
, it follows that ![]() . But now since all terms of
. But now since all terms of ![]() are guaranteed to be nonnegative, this entire expression cannot be negative, leading to a contradiction. Therefore,
are guaranteed to be nonnegative, this entire expression cannot be negative, leading to a contradiction. Therefore, ![]() is acute.
is acute.
See also
| 2001 USAMO (Problems • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









