Difference between revisions of "2003 AMC 12A Problems"
(→Problem 9: added problem) |
Cinnamon e (talk | contribs) m (→Problem 22) |
||
| (36 intermediate revisions by 19 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{AMC12 Problems|year=2003|ab=A}} | ||
== Problem 1 == | == Problem 1 == | ||
What is the difference between the sum of the first <math>2003</math> even counting numbers and the sum of the first <math>2003</math> odd counting numbers? | What is the difference between the sum of the first <math>2003</math> even counting numbers and the sum of the first <math>2003</math> odd counting numbers? | ||
| Line 7: | Line 8: | ||
== Problem 2 == | == Problem 2 == | ||
| − | Members of the Rockham Soccer | + | Members of the Rockham Soccer League buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the League? |
<math> \mathrm{(A) \ } 77\qquad \mathrm{(B) \ } 91\qquad \mathrm{(C) \ } 143\qquad \mathrm{(D) \ } 182\qquad \mathrm{(E) \ } 286 </math> | <math> \mathrm{(A) \ } 77\qquad \mathrm{(B) \ } 91\qquad \mathrm{(C) \ } 143\qquad \mathrm{(D) \ } 182\qquad \mathrm{(E) \ } 286 </math> | ||
| Line 57: | Line 58: | ||
== Problem 8 == | == Problem 8 == | ||
| − | What is the probability that a randomly drawn positive factor of <math>60</math> is less than <math>7</math> | + | What is the probability that a randomly drawn positive factor of <math>60</math> is less than <math>7</math>? |
<math> \mathrm{(A) \ } \frac{1}{10}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{1}{4}\qquad \mathrm{(D) \ } \frac{1}{3}\qquad \mathrm{(E) \ } \frac{1}{2} </math> | <math> \mathrm{(A) \ } \frac{1}{10}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{1}{4}\qquad \mathrm{(D) \ } \frac{1}{3}\qquad \mathrm{(E) \ } \frac{1}{2} </math> | ||
| Line 65: | Line 66: | ||
== Problem 9 == | == Problem 9 == | ||
| − | A set <math>S</math> of points in the <math>xy</math>-plane is symmetric about the | + | A set <math>S</math> of points in the <math>xy</math>-plane is symmetric about the origin, both coordinate axes, and the line <math>y=x</math>. If <math>(2,3)</math> is in <math>S</math>, what is the smallest number of points in <math>S</math>? |
<math> \mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 8\qquad \mathrm{(E) \ } 16 </math> | <math> \mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 8\qquad \mathrm{(E) \ } 16 </math> | ||
| Line 72: | Line 73: | ||
== Problem 10 == | == Problem 10 == | ||
| + | |||
| + | Al, Bert, and Carl are the winners of a school drawing for a pile of Halloween candy, which they are to divide in a ratio of <math>3:2:1</math>, respectively. Due to some confusion they come at different times to claim their prizes, and each assumes he is the first to arrive. If each takes what he believes to be the correct share of candy, what fraction of the candy goes unclaimed? | ||
| + | |||
| + | <math> \mathrm{(A) \ } \frac{1}{18}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{2}{9}\qquad \mathrm{(D) \ } \frac{5}{18}\qquad \mathrm{(E) \ } \frac{5}{12} </math> | ||
[[2003 AMC 12A Problems/Problem 10|Solution]] | [[2003 AMC 12A Problems/Problem 10|Solution]] | ||
== Problem 11 == | == Problem 11 == | ||
| + | |||
| + | A square and an equilateral triangle have the same perimeter. Let <math>A</math> be the area of the circle circumscribed about the square and <math>B</math> the area of the circle circumscribed around the triangle. Find <math>A/B</math>. | ||
| + | |||
| + | <math> \mathrm{(A) \ } \frac{9}{16}\qquad \mathrm{(B) \ } \frac{3}{4}\qquad \mathrm{(C) \ } \frac{27}{32}\qquad \mathrm{(D) \ } \frac{3\sqrt{6}}{8}\qquad \mathrm{(E) \ } 1 </math> | ||
[[2003 AMC 12A Problems/Problem 11|Solution]] | [[2003 AMC 12A Problems/Problem 11|Solution]] | ||
| Line 87: | Line 96: | ||
== Problem 13 == | == Problem 13 == | ||
| − | The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is | + | The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing? |
[[Image:2003amc10a10.gif]] | [[Image:2003amc10a10.gif]] | ||
| Line 96: | Line 105: | ||
== Problem 14 == | == Problem 14 == | ||
| + | |||
| + | Points <math>K, L, M,</math> and <math>N</math> lie in the plane of the square <math>ABCD</math> such that <math>AKB</math>, <math>BLC</math>, <math>CMD</math>, and <math>DNA</math> are equilateral triangles. If <math>ABCD</math> has an area of 16, find the area of <math>KLMN</math>. | ||
| + | |||
| + | <asy> | ||
| + | unitsize(2cm); | ||
| + | defaultpen(fontsize(8)+linewidth(0.8)); | ||
| + | pair A=(-0.5,0.5), B=(0.5,0.5), C=(0.5,-0.5), D=(-0.5,-0.5); | ||
| + | pair K=(0,1.366), L=(1.366,0), M=(0,-1.366), N=(-1.366,0); | ||
| + | draw(A--N--K--A--B--K--L--B--C--L--M--C--D--M--N--D--A); | ||
| + | label("$A$",A,SE); | ||
| + | label("$B$",B,SW); | ||
| + | label("$C$",C,NW); | ||
| + | label("$D$",D,NE); | ||
| + | label("$K$",K,NNW); | ||
| + | label("$L$",L,E); | ||
| + | label("$M$",M,S); | ||
| + | label("$N$",N,W); | ||
| + | </asy> | ||
| + | |||
| + | <math> \textrm{(A)}\ 32\qquad\textrm{(B)}\ 16+16\sqrt{3}\qquad\textrm{(C)}\ 48\qquad\textrm{(D)}\ 32+16\sqrt{3}\qquad\textrm{(E)}\ 64 </math> | ||
[[2003 AMC 12A Problems/Problem 14|Solution]] | [[2003 AMC 12A Problems/Problem 14|Solution]] | ||
| Line 109: | Line 138: | ||
== Problem 16 == | == Problem 16 == | ||
| + | |||
| + | A point P is chosen at random in the interior of equilateral triangle <math>ABC</math>. What is the probability that <math>\triangle ABP</math> has a greater area than each of <math>\triangle ACP</math> and <math>\triangle BCP</math>? | ||
| + | |||
| + | <math> \textbf{(A)}\ \frac{1}{6}\qquad\textbf{(B)}\ \frac{1}{4}\qquad\textbf{(C)}\ \frac{1}{3}\qquad\textbf{(D)}\ \frac{1}{2}\qquad\textbf{(E)}\ \frac{2}{3} </math> | ||
[[2003 AMC 12A Problems/Problem 16|Solution]] | [[2003 AMC 12A Problems/Problem 16|Solution]] | ||
| Line 114: | Line 147: | ||
== Problem 17 == | == Problem 17 == | ||
| − | Square <math>ABCD</math> has sides of length <math>4</math>, and <math>M</math> is the midpoint of <math>\overline{CD}</math>. A circle with radius <math>2</math> and center <math>M</math> intersects a circle with | + | Square <math>ABCD</math> has sides of length <math>4</math>, and <math>M</math> is the midpoint of <math>\overline{CD}</math>. A circle with radius <math>2</math> and center <math>M</math> intersects a circle with radius <math>4</math> and center <math>A</math> at points <math>P</math> and <math>D</math>. What is the distance from <math>P</math> to <math>\overline{AD}</math>? |
| − | + | <asy> | |
| + | pair A,B,C,D,M,P; | ||
| + | D=(0,0); | ||
| + | C=(10,0); | ||
| + | B=(10,10); | ||
| + | A=(0,10); | ||
| + | M=(5,0); | ||
| + | P=(8,4); | ||
| + | dot(M); | ||
| + | dot(P); | ||
| + | draw(A--B--C--D--cycle,linewidth(0.7)); | ||
| + | draw((5,5)..D--C..cycle,linewidth(0.7)); | ||
| + | draw((7.07,2.93)..B--A--D..cycle,linewidth(0.7)); | ||
| + | label("$A$",A,NW); | ||
| + | label("$B$",B,NE); | ||
| + | label("$C$",C,SE); | ||
| + | label("$D$",D,SW); | ||
| + | label("$M$",M,S); | ||
| + | label("$P$",P,N); | ||
| + | </asy> | ||
<math>\textbf{(A)}\ 3 \qquad \textbf{(B)}\ \frac {16}{5} \qquad \textbf{(C)}\ \frac {13}{4} \qquad \textbf{(D)}\ 2\sqrt {3} \qquad \textbf{(E)}\ \frac {7}{2}</math> | <math>\textbf{(A)}\ 3 \qquad \textbf{(B)}\ \frac {16}{5} \qquad \textbf{(C)}\ \frac {13}{4} \qquad \textbf{(D)}\ 2\sqrt {3} \qquad \textbf{(E)}\ \frac {7}{2}</math> | ||
| Line 130: | Line 182: | ||
== Problem 19 == | == Problem 19 == | ||
| + | |||
| + | A parabola with equation <math>y=ax^2+bx+c</math> is reflected about the <math>x</math>-axis. The parabola and its reflection are translated horizontally five units in opposite directions to become the graphs of <math>y=f(x)</math> and <math>y=g(x)</math>, respectively. Which of the following describes the graph of <math>y=(f+g)(x)</math>? | ||
| + | |||
| + | <math> \textbf{(A)}\ \text{a parabola tangent to the }x\text{-axis} </math> | ||
| + | <math> \textbf{(B)}\ \text{a parabola not tangent to the }x\text{-axis}\qquad\textbf{(C)}\ \text{a horizontal line} </math> | ||
| + | <math> \textbf{(D)}\ \text{a non-horizontal line}\qquad\textbf{(E)}\ \text{the graph of a cubic function} </math> | ||
[[2003 AMC 12A Problems/Problem 19|Solution]] | [[2003 AMC 12A Problems/Problem 19|Solution]] | ||
== Problem 20 == | == Problem 20 == | ||
| + | |||
| + | How many <math>15</math>-letter arrangements of <math>5</math> A's, <math>5</math> B's, and <math>5</math> C's have no A's in the first <math>5</math> letters, no B's in the next <math>5</math> letters, and no C's in the last <math>5</math> letters? | ||
| + | |||
| + | <math> \textrm{(A)}\ \sum_{k=0}^{5}\binom{5}{k}^{3}\qquad\textrm{(B)}\ 3^{5}\cdot 2^{5}\qquad\textrm{(C)}\ 2^{15}\qquad\textrm{(D)}\ \frac{15!}{(5!)^{3}}\qquad\textrm{(E)}\ 3^{15} </math> | ||
[[2003 AMC 12A Problems/Problem 20|Solution]] | [[2003 AMC 12A Problems/Problem 20|Solution]] | ||
| Line 149: | Line 211: | ||
== Problem 22 == | == Problem 22 == | ||
| + | |||
| + | Objects <math>A</math> and <math>B</math> move simultaneously in the coordinate plane via a sequence of steps, each of length one. Object <math>A</math> starts at <math>(0,0)</math> and each of its steps is either right or up, both equally likely. Object <math>B</math> starts at <math>(5,7)</math> and each of its steps is either to the left or down, both equally likely. Which of the following is closest to the probability that the objects meet? | ||
| + | |||
| + | <math> | ||
| + | \mathrm{(A)} \ 0.10 \qquad | ||
| + | \mathrm{(B)} \ 0.15 \qquad | ||
| + | \mathrm{(C)} \ 0.20 \qquad | ||
| + | \mathrm{(D)} \ 0.25 \qquad | ||
| + | \mathrm{(E)} \ 0.30 \qquad | ||
| + | </math> | ||
[[2003 AMC 12A Problems/Problem 22|Solution]] | [[2003 AMC 12A Problems/Problem 22|Solution]] | ||
== Problem 23 == | == Problem 23 == | ||
| + | |||
| + | How many perfect squares are divisors of the product <math>1! \cdot 2! \cdot 3! \cdot \hdots \cdot 9!</math>? | ||
| + | |||
| + | <math> \textbf{(A)}\ 504\qquad\textbf{(B)}\ 672\qquad\textbf{(C)}\ 864\qquad\textbf{(D)}\ 936\qquad\textbf{(E)}\ 1008 </math> | ||
[[2003 AMC 12A Problems/Problem 23|Solution]] | [[2003 AMC 12A Problems/Problem 23|Solution]] | ||
== Problem 24 == | == Problem 24 == | ||
| + | |||
| + | If <math>a\geq b > 1,</math> what is the largest possible value of <math>\log_{a}(a/b) + \log_{b}(b/a)?</math> | ||
| + | |||
| + | <math> | ||
| + | \mathrm{(A)}\ -2 \qquad | ||
| + | \mathrm{(B)}\ 0 \qquad | ||
| + | \mathrm{(C)}\ 2 \qquad | ||
| + | \mathrm{(D)}\ 3 \qquad | ||
| + | \mathrm{(E)}\ 4 | ||
| + | </math> | ||
[[2003 AMC 12A Problems/Problem 24|Solution]] | [[2003 AMC 12A Problems/Problem 24|Solution]] | ||
== Problem 25 == | == Problem 25 == | ||
| − | Let <math> | + | Let <math>f(x)= \sqrt{ax^2+bx} </math>. For how many real values of <math>a</math> is there at least one positive value of <math> b </math> for which the domain of <math>f </math> and the range of <math> f </math> are the same set? |
<math> \mathrm{(A) \ 0 } \qquad \mathrm{(B) \ 1 } \qquad \mathrm{(C) \ 2 } \qquad \mathrm{(D) \ 3 } \qquad \mathrm{(E) \ \mathrm{infinitely \ many} } </math> | <math> \mathrm{(A) \ 0 } \qquad \mathrm{(B) \ 1 } \qquad \mathrm{(C) \ 2 } \qquad \mathrm{(D) \ 3 } \qquad \mathrm{(E) \ \mathrm{infinitely \ many} } </math> | ||
| Line 168: | Line 254: | ||
== See also == | == See also == | ||
| + | |||
| + | {{AMC12 box|year=2003|ab=A|before=[[2002 AMC 12B Problems]]|after=[[2003 AMC 12B Problems]]}} | ||
| + | |||
* [[AMC 12]] | * [[AMC 12]] | ||
* [[AMC 12 Problems and Solutions]] | * [[AMC 12 Problems and Solutions]] | ||
* [[2003 AMC 12A]] | * [[2003 AMC 12A]] | ||
* [[Mathematics competition resources]] | * [[Mathematics competition resources]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 20:06, 19 August 2023
| 2003 AMC 12A (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
What is the difference between the sum of the first ![]() even counting numbers and the sum of the first
even counting numbers and the sum of the first ![]() odd counting numbers?
odd counting numbers?
![]()
Problem 2
Members of the Rockham Soccer League buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the League?
![]()
Problem 3
A solid box is ![]() cm by
cm by ![]() cm by
cm by ![]() cm. A new solid is formed by removing a cube
cm. A new solid is formed by removing a cube ![]() cm on a side from each corner of this box. What percent of the original volume is removed?
cm on a side from each corner of this box. What percent of the original volume is removed?
![]()
Problem 4
It takes Mary ![]() minutes to walk uphill
minutes to walk uphill ![]() km from her home to school, but it takes her only
km from her home to school, but it takes her only ![]() minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?
minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?
![]()
Problem 5
The sum of the two 5-digit numbers ![]() and
and ![]() is
is ![]() . What is
. What is ![]() ?
?
![]()
Problem 6
Define ![]() to be
to be ![]() for all real numbers
for all real numbers ![]() and
and ![]() . Which of the following statements is not true?
. Which of the following statements is not true?
![]() for all
for all ![]() and
and ![]()
![]() for all
for all ![]() and
and ![]()
![]() for all
for all ![]()
![]() for all
for all ![]()
![]() if
if ![]()
Problem 7
How many non-congruent triangles with perimeter ![]() have integer side lengths?
have integer side lengths?
![]()
Problem 8
What is the probability that a randomly drawn positive factor of ![]() is less than
is less than ![]() ?
?
![]()
Problem 9
A set ![]() of points in the
of points in the ![]() -plane is symmetric about the origin, both coordinate axes, and the line
-plane is symmetric about the origin, both coordinate axes, and the line ![]() . If
. If ![]() is in
is in ![]() , what is the smallest number of points in
, what is the smallest number of points in ![]() ?
?
![]()
Problem 10
Al, Bert, and Carl are the winners of a school drawing for a pile of Halloween candy, which they are to divide in a ratio of ![]() , respectively. Due to some confusion they come at different times to claim their prizes, and each assumes he is the first to arrive. If each takes what he believes to be the correct share of candy, what fraction of the candy goes unclaimed?
, respectively. Due to some confusion they come at different times to claim their prizes, and each assumes he is the first to arrive. If each takes what he believes to be the correct share of candy, what fraction of the candy goes unclaimed?
![]()
Problem 11
A square and an equilateral triangle have the same perimeter. Let ![]() be the area of the circle circumscribed about the square and
be the area of the circle circumscribed about the square and ![]() the area of the circle circumscribed around the triangle. Find
the area of the circle circumscribed around the triangle. Find ![]() .
.
![]()
Problem 12
Sally has five red cards numbered ![]() through
through ![]() and four blue cards numbered
and four blue cards numbered ![]() through
through ![]() . She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?
. She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?
![]()
Problem 13
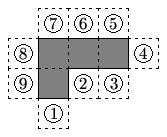
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?
![]()
Problem 14
Points ![]() and
and ![]() lie in the plane of the square
lie in the plane of the square ![]() such that
such that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are equilateral triangles. If
are equilateral triangles. If ![]() has an area of 16, find the area of
has an area of 16, find the area of ![]() .
.
![[asy] unitsize(2cm); defaultpen(fontsize(8)+linewidth(0.8)); pair A=(-0.5,0.5), B=(0.5,0.5), C=(0.5,-0.5), D=(-0.5,-0.5); pair K=(0,1.366), L=(1.366,0), M=(0,-1.366), N=(-1.366,0); draw(A--N--K--A--B--K--L--B--C--L--M--C--D--M--N--D--A); label("$A$",A,SE); label("$B$",B,SW); label("$C$",C,NW); label("$D$",D,NE); label("$K$",K,NNW); label("$L$",L,E); label("$M$",M,S); label("$N$",N,W); [/asy]](http://latex.artofproblemsolving.com/1/4/0/14057a8f4f08bad17471fdaed56a758f1e2fcea7.png)
![]()
Problem 15
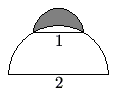
A semicircle of diameter ![]() sits at the top of a semicircle of diameter
sits at the top of a semicircle of diameter ![]() , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
, as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
![]()
Problem 16
A point P is chosen at random in the interior of equilateral triangle ![]() . What is the probability that
. What is the probability that ![]() has a greater area than each of
has a greater area than each of ![]() and
and ![]() ?
?
![]()
Problem 17
Square ![]() has sides of length
has sides of length ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . A circle with radius
. A circle with radius ![]() and center
and center ![]() intersects a circle with radius
intersects a circle with radius ![]() and center
and center ![]() at points
at points ![]() and
and ![]() . What is the distance from
. What is the distance from ![]() to
to ![]() ?
?
![[asy] pair A,B,C,D,M,P; D=(0,0); C=(10,0); B=(10,10); A=(0,10); M=(5,0); P=(8,4); dot(M); dot(P); draw(A--B--C--D--cycle,linewidth(0.7)); draw((5,5)..D--C..cycle,linewidth(0.7)); draw((7.07,2.93)..B--A--D..cycle,linewidth(0.7)); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,SE); label("$D$",D,SW); label("$M$",M,S); label("$P$",P,N); [/asy]](http://latex.artofproblemsolving.com/b/1/f/b1f5dc5a294bcfb2e9f16e90d2d7b6f5843d52e1.png)
![]()
Problem 18
Let ![]() be a
be a ![]() -digit number, and let
-digit number, and let ![]() and
and ![]() be the quotient and the remainder, respectively, when
be the quotient and the remainder, respectively, when ![]() is divided by
is divided by ![]() . For how many values of
. For how many values of ![]() is
is ![]() divisible by
divisible by ![]() ?
?
![]()
Problem 19
A parabola with equation ![]() is reflected about the
is reflected about the ![]() -axis. The parabola and its reflection are translated horizontally five units in opposite directions to become the graphs of
-axis. The parabola and its reflection are translated horizontally five units in opposite directions to become the graphs of ![]() and
and ![]() , respectively. Which of the following describes the graph of
, respectively. Which of the following describes the graph of ![]() ?
?
![]()
![]()
![]()
Problem 20
How many ![]() -letter arrangements of
-letter arrangements of ![]() A's,
A's, ![]() B's, and
B's, and ![]() C's have no A's in the first
C's have no A's in the first ![]() letters, no B's in the next
letters, no B's in the next ![]() letters, and no C's in the last
letters, and no C's in the last ![]() letters?
letters?

Problem 21
The graph of the polynomial
![]()
has five distinct ![]() -intercepts, one of which is at
-intercepts, one of which is at ![]() . Which of the following coefficients cannot be zero?
. Which of the following coefficients cannot be zero?
![]()
Problem 22
Objects ![]() and
and ![]() move simultaneously in the coordinate plane via a sequence of steps, each of length one. Object
move simultaneously in the coordinate plane via a sequence of steps, each of length one. Object ![]() starts at
starts at ![]() and each of its steps is either right or up, both equally likely. Object
and each of its steps is either right or up, both equally likely. Object ![]() starts at
starts at ![]() and each of its steps is either to the left or down, both equally likely. Which of the following is closest to the probability that the objects meet?
and each of its steps is either to the left or down, both equally likely. Which of the following is closest to the probability that the objects meet?
![]()
Problem 23
How many perfect squares are divisors of the product ![]() ?
?
![]()
Problem 24
If ![]() what is the largest possible value of
what is the largest possible value of ![]()
![]()
Problem 25
Let ![]() . For how many real values of
. For how many real values of ![]() is there at least one positive value of
is there at least one positive value of ![]() for which the domain of
for which the domain of ![]() and the range of
and the range of ![]() are the same set?
are the same set?
![]()
See also
| 2003 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by 2002 AMC 12B Problems |
Followed by 2003 AMC 12B Problems |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()