Difference between revisions of "2020 AMC 12A Problems/Problem 17"
m (Minor mistake) |
|||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 5: | Line 5: | ||
== Solution 1 == | == Solution 1 == | ||
| − | Let the coordinates of the quadrilateral be <math>(n,\ln(n)),(n+1,\ln(n+1)),(n+2,\ln(n+2)),(n+3,\ln(n+3))</math>. We have by shoelace's theorem, that the area is<cmath>\frac{\ln(n)(n+1) + \ln(n+1)(n+2) + \ln(n+2)(n+3)+n\ln(n+3)}{2} - \frac{\ln(n+1)(n) + \ln(n+2)(n+1) + \ln(n+3)(n+2)+\ln(n)(n+3)}{2}= | + | Let the coordinates of the quadrilateral be <math>(n,\ln(n)),(n+1,\ln(n+1)),(n+2,\ln(n+2)),(n+3,\ln(n+3))</math>. We have by shoelace's theorem, that the area is |
| + | <cmath>\begin{align*} | ||
| + | &\frac{\ln(n)(n+1) + \ln(n+1)(n+2) + \ln(n+2)(n+3)+n\ln(n+3)}{2} - \frac{\ln(n+1)(n) + \ln(n+2)(n+1) + \ln(n+3)(n+2)+\ln(n)(n+3)}{2} \ | ||
| + | &=\frac{\ln \left( \frac{n^{n+1}(n+1)^{n+2}(n+2)^{n+3}(n+3)^n}{(n+1)^n(n+2)^{n+1}(n+3)^{n+2}n^{n+3}}\right)}{2} \ | ||
| + | &= \ln \left( \sqrt{\frac{(n+1)^2(n+2)^2}{n^2(n+3)^2}} \right) \ | ||
| + | &= \ln \left(\frac{(n+1)(n+2)}{n(n+3)}\right) \ | ||
| + | &= \ln \left( \frac{91}{90} \right). | ||
| + | \end{align*}</cmath> | ||
| + | We know that the numerator must have a factor of <math>13</math>, so given the answer choices, <math>n</math> is either <math>12</math> or <math>11</math>. If <math>n=11</math>, the expression <math>\frac{(n+1)(n+2)}{n(n+3)}</math> does not evaluate to <math>\frac{91}{90}</math>, but if <math>n=12</math>, the expression evaluates to <math>\frac{91}{90}</math>. Hence, our answer is <math>\boxed{12}</math>. | ||
== Solution 2 == | == Solution 2 == | ||
| − | Like above, use the shoelace formula to find that the area of the | + | Like above, use the shoelace formula to find that the area of the quadrilateral is equal to <math>\ln\frac{(n+1)(n+2)}{n(n+3)}</math>. Because the final area we are looking for is <math>\ln\frac{91}{90}</math>, the numerator factors into <math>13</math> and <math>7</math>, which one of <math>n+1</math> and <math>n+2</math> has to be a multiple of <math>13</math> and the other has to be a multiple of <math>7</math>. Clearly, the only choice for that is <math>\boxed{12}</math> |
~Solution by IronicNinja | ~Solution by IronicNinja | ||
| Line 27: | Line 35: | ||
~Solution by AsdrúbalBeltrán | ~Solution by AsdrúbalBeltrán | ||
| − | + | ==Video Solution by TheBeautyofMath== | |
https://www.youtube.com/watch?v=Eq2A2TTahqU?t=583 | https://www.youtube.com/watch?v=Eq2A2TTahqU?t=583 | ||
Another example of shoelace theorem included earlier in the video | Another example of shoelace theorem included earlier in the video | ||
Latest revision as of 20:43, 21 October 2023
Contents
[hide]Problem
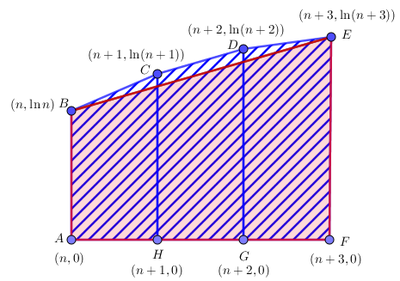
The vertices of a quadrilateral lie on the graph of ![]() , and the
, and the ![]() -coordinates of these vertices are consecutive positive integers. The area of the quadrilateral is
-coordinates of these vertices are consecutive positive integers. The area of the quadrilateral is ![]() . What is the
. What is the ![]() -coordinate of the leftmost vertex?
-coordinate of the leftmost vertex?
![]()
Solution 1
Let the coordinates of the quadrilateral be ![]() . We have by shoelace's theorem, that the area is
. We have by shoelace's theorem, that the area is
 We know that the numerator must have a factor of
We know that the numerator must have a factor of ![]() , so given the answer choices,
, so given the answer choices, ![]() is either
is either ![]() or
or ![]() . If
. If ![]() , the expression
, the expression ![]() does not evaluate to
does not evaluate to ![]() , but if
, but if ![]() , the expression evaluates to
, the expression evaluates to ![]() . Hence, our answer is
. Hence, our answer is ![]() .
.
Solution 2
Like above, use the shoelace formula to find that the area of the quadrilateral is equal to ![]() . Because the final area we are looking for is
. Because the final area we are looking for is ![]() , the numerator factors into
, the numerator factors into ![]() and
and ![]() , which one of
, which one of ![]() and
and ![]() has to be a multiple of
has to be a multiple of ![]() and the other has to be a multiple of
and the other has to be a multiple of ![]() . Clearly, the only choice for that is
. Clearly, the only choice for that is ![]()
~Solution by IronicNinja
Solution 3
How ![]() is a concave function, then:
is a concave function, then:
Therefore ![]() , all quadrilaterals of side right are trapezius
, all quadrilaterals of side right are trapezius
![]()
![]()
![]()
![]()
~Solution by AsdrúbalBeltrán
Video Solution by TheBeautyofMath
https://www.youtube.com/watch?v=Eq2A2TTahqU?t=583 Another example of shoelace theorem included earlier in the video
~IceMatrix
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 16 |
Followed by Problem 18 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.