Difference between revisions of "2019 AIME I Problems/Problem 15"
Mr.sharkman (talk | contribs) m |
|||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 82: | Line 82: | ||
==Solution 6(lazy)== | ==Solution 6(lazy)== | ||
| − | <math>PX \cdot PY=AP \cdot PB=5 \cdot 3=15</math> by power of a point. Also, <math>PX+PY=XY=11</math>, so <math>PX</math> and <math>PY</math> are solutions to the quadratic <math>x^2-11x+15=0</math> so <math>PX</math> and <math>PY</math> is <math>\frac{11\pm\sqrt{61}}{2}</math> in some order. Now, because we want <math>PQ^2</math> and it is known to be rational, we can guess that <math>PQ</math> is irrational or the problem would simply ask for <math>PQ</math>. <math>PQ=QX-PX</math>, and chances are low that <math>QX</math> is some number with a square root plus or minus <math>\frac{\sqrt{61}}{2}</math> to cancel out the <math>\frac{\sqrt{61}}{2}</math> in <math>PX</math>, so one can see that <math>PQ^2</math> is most likely to be <math>(\frac{\sqrt{61}}{2})^2=\frac{61}{4}</math>, and our answer is <math>61+4=\boxed{065}</math> | + | <asy> |
| + | size(8cm); | ||
| + | pair O, A, B, P, O1, O2, Q, X, Y; | ||
| + | O=(0, 0); | ||
| + | A=dir(140); B=dir(40); | ||
| + | P=(3A+5B)/8; | ||
| + | O1=extension((A+P)/2, (A+P)/2+(0, 1), A, O); | ||
| + | O2=extension((B+P)/2, (B+P)/2+(0, 1), B, O); | ||
| + | Q=intersectionpoints(circle(O1, length(A-O1)), circle(O2, length(B-O2)))[1]; | ||
| + | X=intersectionpoint(P -- (P+(P-Q)*100), circle(O, 1)); | ||
| + | Y=intersectionpoint(Q -- (Q+(Q-P)*100), circle(O, 1)); | ||
| + | |||
| + | draw(circle(O, 1)); | ||
| + | draw(circle(O1, length(A-O1))); | ||
| + | draw(circle(O2, length(B-O2))); | ||
| + | draw(A -- B,red); draw(X -- Y,green); | ||
| + | |||
| + | dot("$A$", A, A); | ||
| + | dot("$B$", B, B); | ||
| + | dot("$P$", P, dir(70),blue); | ||
| + | dot("$Q$", Q, dir(200)); | ||
| + | dot("$X$", X, X); | ||
| + | dot("$Y$", Y, Y); | ||
| + | label("$3$", (A+P)/2, N, red); | ||
| + | label("$5$", (B+P)/2, N, red); | ||
| + | draw(brace(X,Y)); | ||
| + | label("$11$",brace(X,Y),dir(20)); | ||
| + | </asy> | ||
| + | <math>PX \cdot PY=AP \cdot PB=5 \cdot 3=15</math> by power of a point. Also, <math>PX+PY=XY=11</math>, so <math>PX</math> and <math>PY</math> are solutions to the quadratic <math>x^2-11x+15=0</math> so <math>PX</math> and <math>PY</math> is <math>\frac{11\pm\sqrt{61}}{2}</math> in some order. Now, because we want <math>PQ^2</math> and it is known to be rational, we can guess that <math>PQ</math> is irrational or the problem would simply ask for <math>PQ</math>. We can also figure out that since <math>PQ^2</math> is rational, <math>PQ</math> is <math>\sqrt{\text{[something]}}</math>. <math>PQ=QX-PX</math>, and chances are low that <math>QX</math> is some number with a square root plus or minus <math>\frac{\sqrt{61}}{2}</math> to cancel out the <math>\frac{\sqrt{61}}{2}</math> in <math>PX</math>, so one can see that <math>PQ^2</math> is most likely to be <math>\left(\frac{\sqrt{61}}{2}\right)^2=\frac{61}{4}</math>, and our answer is <math>61+4=\boxed{065}</math> | ||
Note : If our answer is correct, then <math>QX=\frac{11}{2}</math>, which made <math>Q</math> the midpoint of <math>XY</math>, a feature that occurs often in AIME problems, so that again made our answer probable. Midpoints have many properties and there is a lot of ways to show if a point is the midpoint of a segment. Even if the answer is wrong, it's still the same as leaving it blank and 065 is a good guess. ~[[Ddk001]] | Note : If our answer is correct, then <math>QX=\frac{11}{2}</math>, which made <math>Q</math> the midpoint of <math>XY</math>, a feature that occurs often in AIME problems, so that again made our answer probable. Midpoints have many properties and there is a lot of ways to show if a point is the midpoint of a segment. Even if the answer is wrong, it's still the same as leaving it blank and 065 is a good guess. ~[[Ddk001]] | ||
| Line 90: | Line 118: | ||
<cmath>AP \cdot BP = XP \cdot YP = 15.</cmath> | <cmath>AP \cdot BP = XP \cdot YP = 15.</cmath> | ||
Also, we have <math>XY = XP+YP = 11,</math> so <math>XP = \frac{11 \pm \sqrt{61}}{2}</math>. Notice that <math>XQ = \frac{XY}{2} = \frac{11}{2},</math> so <math>PQ = \frac{\sqrt{61}}{2},</math> giving us our answer of <math>\boxed{065}.</math> | Also, we have <math>XY = XP+YP = 11,</math> so <math>XP = \frac{11 \pm \sqrt{61}}{2}</math>. Notice that <math>XQ = \frac{XY}{2} = \frac{11}{2},</math> so <math>PQ = \frac{\sqrt{61}}{2},</math> giving us our answer of <math>\boxed{065}.</math> | ||
| + | |||
| + | |||
| + | ==Solution 8== | ||
| + | |||
| + | [[File:2019_AIME_Problem_15_Diagram.png|400px|thumb|right|[https://www.overleaf.com/read/bkdngbhwcskc#415c3f Latex]]] | ||
| + | |||
| + | Like Solution 7, let <math>Q'</math> be the altitude from <math>O</math> to <math>XY</math>. And, let <math>M</math> be the intersection of <math>O_1O_2</math> and <math>PQ</math>. Construct <math>P'</math> on line <math>AO</math> such that <math>PP' \parallel O_2O_1</math>. First, because of isosceles triangles <math>OAB</math>, <math>O_1AP</math>, and <math>O_2BP</math>, we have <math>\angle{OAP} = \angle{OBA} = \angle{APO_1} = \angle{BPO_2}</math>, which means <math>OO_1PO_2</math> is a parallelogram. So, <math>O_2P = OO_1</math>. It is also clear that <math>PP'O_1O_2</math> is a parallelogram by virtue of our definition. Thus, <math>O_2P = O_1P' = OO_1</math>. Since <math>OQ' \parallel O_1O_2 \parallel P'P</math> (because of the right angles), <math>\frac{Q'M}{MP} = \frac{OO_1}{O_1P'} = 1 \implies Q'M = MP</math>. And, because <math>QM = MP</math>, <math>Q = Q'</math>. From Power of a Point on <math>P</math>, we have <math>XP(11-XP) = 15</math>, giving us <math>XP = \frac{11 - \sqrt{61}}{2}</math>. Since <math>OQ</math> is perpendicular to <math>XY</math>, <math>Q</math> is the midpoint of <math>XY</math>, so <math>XQ = \frac{11}{2}</math>. Thus, <math>PQ = \frac{11}{2} - \frac{11 - \sqrt{61}}{2} = \frac{\sqrt{61}}{2} \implies {PQ}^2 = \frac{61}{4}</math>. Therefore, our answer is <math>\boxed{65}</math>. | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Crazyvideogamez CrazyVideoGamez] | ||
| + | |||
| + | <math> | ||
| + | \newline | ||
| + | </math> | ||
| + | |||
| + | ==Video Solution by Mr. Math== | ||
| + | |||
| + | https://www.youtube.com/watch?v=X_CSRwUh0Rc | ||
==See Also== | ==See Also== | ||
Revision as of 10:32, 1 February 2024
Contents
[hide]Problem
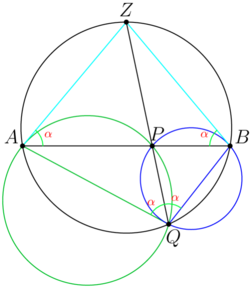
Let ![]() be a chord of a circle
be a chord of a circle ![]() , and let
, and let ![]() be a point on the chord
be a point on the chord ![]() . Circle
. Circle ![]() passes through
passes through ![]() and
and ![]() and is internally tangent to
and is internally tangent to ![]() . Circle
. Circle ![]() passes through
passes through ![]() and
and ![]() and is internally tangent to
and is internally tangent to ![]() . Circles
. Circles ![]() and
and ![]() intersect at points
intersect at points ![]() and
and ![]() . Line
. Line ![]() intersects
intersects ![]() at
at ![]() and
and ![]() . Assume that
. Assume that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
![[asy] size(8cm); pair O, A, B, P, O1, O2, Q, X, Y; O=(0, 0); A=dir(140); B=dir(40); P=(3A+5B)/8; O1=extension((A+P)/2, (A+P)/2+(0, 1), A, O); O2=extension((B+P)/2, (B+P)/2+(0, 1), B, O); Q=intersectionpoints(circle(O1, length(A-O1)), circle(O2, length(B-O2)))[1]; X=intersectionpoint(P -- (P+(P-Q)*100), circle(O, 1)); Y=intersectionpoint(Q -- (Q+(Q-P)*100), circle(O, 1)); draw(circle(O, 1)); draw(circle(O1, length(A-O1))); draw(circle(O2, length(B-O2))); draw(A -- B); draw(X -- Y); draw(A -- O -- B); draw(O1 -- P -- O2); dot("$O$", O, S); dot("$A$", A, A); dot("$B$", B, B); dot("$P$", P, dir(70)); dot("$Q$", Q, dir(200)); dot("$O_1$", O1, SW); dot("$O_2$", O2, SE); dot("$X$", X, X); dot("$Y$", Y, Y); [/asy]](http://latex.artofproblemsolving.com/e/9/6/e962da47468c53887e591467b64d5b0b0fe4dde6.png) Let
Let ![]() and
and ![]() be the centers of
be the centers of ![]() and
and ![]() , respectively. There is a homothety at
, respectively. There is a homothety at ![]() sending
sending ![]() to
to ![]() that sends
that sends ![]() to
to ![]() and
and ![]() to
to ![]() , so
, so ![]() . Similarly,
. Similarly, ![]() , so
, so ![]() is a parallelogram. Moreover,
is a parallelogram. Moreover, ![]() whence
whence ![]() is cyclic. However,
is cyclic. However, ![]() so
so ![]() is an isosceles trapezoid. Since
is an isosceles trapezoid. Since ![]() ,
, ![]() , so
, so ![]() is the midpoint of
is the midpoint of ![]() .
.
By Power of a Point, ![]() . Since
. Since ![]() and
and ![]() ,
, ![]() and the requested sum is
and the requested sum is ![]() .
.
(Solution by TheUltimate123)
Note
One may solve for ![]() first using PoAP,
first using PoAP, ![]() . Then, notice that
. Then, notice that ![]() is rational but
is rational but ![]() is not, also
is not, also ![]() . The most likely explanation for this is that
. The most likely explanation for this is that ![]() is the midpoint of
is the midpoint of ![]() , so that
, so that ![]() and
and ![]() . Then our answer is
. Then our answer is ![]() . One can rigorously prove this using the methods above
. One can rigorously prove this using the methods above
Solution 2
Let the tangents to ![]() at
at ![]() and
and ![]() intersect at
intersect at ![]() . Then, since
. Then, since ![]() ,
, ![]() lies on the radical axis of
lies on the radical axis of ![]() and
and ![]() , which is
, which is ![]() . It follows that
. It follows that ![]() Let
Let ![]() denote the midpoint of
denote the midpoint of ![]() . By the Midpoint of Harmonic Bundles Lemma(EGMO 9.17),
. By the Midpoint of Harmonic Bundles Lemma(EGMO 9.17), ![]() whence
whence ![]() . Like above,
. Like above, ![]() . Since
. Since ![]() , we establish that
, we establish that ![]() , from which
, from which ![]() , and the requested sum is
, and the requested sum is ![]() .
.
(Solution by TheUltimate123)
Solution 3
Firstly we need to notice that ![]() is the middle point of
is the middle point of ![]() . Assume the center of circle
. Assume the center of circle ![]() are
are ![]() , respectively. Then
, respectively. Then ![]() are collinear and
are collinear and ![]() are collinear. Link
are collinear. Link ![]() . Notice that,
. Notice that, ![]() . As a result,
. As a result, ![]() and
and ![]() . So we have parallelogram
. So we have parallelogram ![]() . So
. So ![]() Notice that,
Notice that, ![]() and
and ![]() divides
divides ![]() into two equal length pieces, So we have
into two equal length pieces, So we have ![]() . As a result,
. As a result, ![]() lie on one circle. So
lie on one circle. So ![]() . Notice that since
. Notice that since ![]() , we have
, we have ![]() . As a result,
. As a result, ![]() . So
. So ![]() is the middle point of
is the middle point of ![]() .
.
Back to our problem. Assume ![]() ,
, ![]() and
and ![]() . Then we have
. Then we have ![]() , that is,
, that is, ![]() . Also,
. Also, ![]() . Solve these above, we have
. Solve these above, we have ![]() . As a result, we have
. As a result, we have ![]() . So, we have
. So, we have ![]() . As a result, our answer is
. As a result, our answer is ![]() .
.
Solution By BladeRunnerAUG (Fanyuchen20020715). Edited by bgn4493.
Solution 4
Note that the tangents to the circles at ![]() and
and ![]() intersect at a point
intersect at a point ![]() on
on ![]() by radical axis theorem. Since
by radical axis theorem. Since ![]() and
and ![]() , we have
, we have
![]() so
so ![]() is cyclic.
is cyclic.
But if ![]() is the center of
is the center of ![]() , clearly
, clearly ![]() is cyclic with diameter
is cyclic with diameter ![]() , so
, so ![]() implies that
implies that ![]() is the midpoint of
is the midpoint of ![]() . Then, by power of point
. Then, by power of point ![]() ,
, ![]() whereas it is given that
whereas it is given that ![]() . Thus
. Thus ![]() so
so ![]() , i.e.
, i.e. ![]() and the answer is
and the answer is ![]() .
.
Solution 5
Connect ![]() , since
, since ![]() , so
, so ![]() then, so
then, so ![]() are concyclic
are concyclic
We let ![]() , it is clear that
, it is clear that ![]() , which leads to the conclusion
, which leads to the conclusion ![]() which tells
which tells ![]() is the midpoint of
is the midpoint of ![]()
Then it is clear, ![]() , the answer is
, the answer is ![]()
~bluesoul
Solution 6(lazy)
![[asy] size(8cm); pair O, A, B, P, O1, O2, Q, X, Y; O=(0, 0); A=dir(140); B=dir(40); P=(3A+5B)/8; O1=extension((A+P)/2, (A+P)/2+(0, 1), A, O); O2=extension((B+P)/2, (B+P)/2+(0, 1), B, O); Q=intersectionpoints(circle(O1, length(A-O1)), circle(O2, length(B-O2)))[1]; X=intersectionpoint(P -- (P+(P-Q)*100), circle(O, 1)); Y=intersectionpoint(Q -- (Q+(Q-P)*100), circle(O, 1)); draw(circle(O, 1)); draw(circle(O1, length(A-O1))); draw(circle(O2, length(B-O2))); draw(A -- B,red); draw(X -- Y,green); dot("$A$", A, A); dot("$B$", B, B); dot("$P$", P, dir(70),blue); dot("$Q$", Q, dir(200)); dot("$X$", X, X); dot("$Y$", Y, Y); label("$3$", (A+P)/2, N, red); label("$5$", (B+P)/2, N, red); draw(brace(X,Y)); label("$11$",brace(X,Y),dir(20)); [/asy]](http://latex.artofproblemsolving.com/0/2/1/021866f4c98be05cd2670be35b844ab217fc247b.png)
![]() by power of a point. Also,
by power of a point. Also, ![]() , so
, so ![]() and
and ![]() are solutions to the quadratic
are solutions to the quadratic ![]() so
so ![]() and
and ![]() is
is ![]() in some order. Now, because we want
in some order. Now, because we want ![]() and it is known to be rational, we can guess that
and it is known to be rational, we can guess that ![]() is irrational or the problem would simply ask for
is irrational or the problem would simply ask for ![]() . We can also figure out that since
. We can also figure out that since ![]() is rational,
is rational, ![]() is
is ![]() .
. ![]() , and chances are low that
, and chances are low that ![]() is some number with a square root plus or minus
is some number with a square root plus or minus ![]() to cancel out the
to cancel out the ![]() in
in ![]() , so one can see that
, so one can see that ![]() is most likely to be
is most likely to be  , and our answer is
, and our answer is ![]()
Note : If our answer is correct, then ![]() , which made
, which made ![]() the midpoint of
the midpoint of ![]() , a feature that occurs often in AIME problems, so that again made our answer probable. Midpoints have many properties and there is a lot of ways to show if a point is the midpoint of a segment. Even if the answer is wrong, it's still the same as leaving it blank and 065 is a good guess. ~Ddk001
, a feature that occurs often in AIME problems, so that again made our answer probable. Midpoints have many properties and there is a lot of ways to show if a point is the midpoint of a segment. Even if the answer is wrong, it's still the same as leaving it blank and 065 is a good guess. ~Ddk001
Solution 7
We will show that ![]() is the midpoint of
is the midpoint of ![]() To do this, let
To do this, let ![]() be the altitude from
be the altitude from ![]() to
to ![]() or, equivalently, to
or, equivalently, to ![]() Notice that
Notice that ![]() is a parallelogram. Thus, the height from
is a parallelogram. Thus, the height from ![]() to
to ![]() is equal to the height from
is equal to the height from ![]() to
to ![]() Say that the line through
Say that the line through ![]() perpendicular to
perpendicular to ![]() intersects
intersects ![]() at
at ![]() Then,
Then, ![]() is perpendicular to
is perpendicular to ![]() so
so ![]() is on
is on ![]() Now, we have that the altitude from
Now, we have that the altitude from ![]() to
to ![]() is equal to the altitude from
is equal to the altitude from ![]() to
to ![]() (since
(since ![]() ). However, the altitude from
). However, the altitude from ![]() to
to ![]() is just
is just ![]() Also, the altitude from
Also, the altitude from ![]() to
to ![]() is
is ![]() , so
, so ![]() Thus,
Thus, ![]() bisects
bisects ![]() However, this is true for
However, this is true for ![]() too, so
too, so ![]() and we are done. Now, by PoP, we have
and we are done. Now, by PoP, we have
![]() Also, we have
Also, we have ![]() so
so ![]() . Notice that
. Notice that ![]() so
so ![]() giving us our answer of
giving us our answer of ![]()
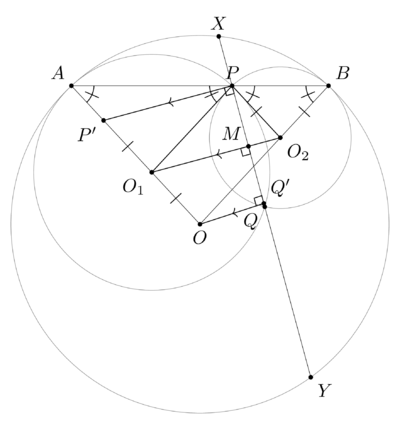
Solution 8
Like Solution 7, let ![]() be the altitude from
be the altitude from ![]() to
to ![]() . And, let
. And, let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Construct
. Construct ![]() on line
on line ![]() such that
such that ![]() . First, because of isosceles triangles
. First, because of isosceles triangles ![]() ,
, ![]() , and
, and ![]() , we have
, we have ![]() , which means
, which means ![]() is a parallelogram. So,
is a parallelogram. So, ![]() . It is also clear that
. It is also clear that ![]() is a parallelogram by virtue of our definition. Thus,
is a parallelogram by virtue of our definition. Thus, ![]() . Since
. Since ![]() (because of the right angles),
(because of the right angles), ![]() . And, because
. And, because ![]() ,
, ![]() . From Power of a Point on
. From Power of a Point on ![]() , we have
, we have ![]() , giving us
, giving us ![]() . Since
. Since ![]() is perpendicular to
is perpendicular to ![]() ,
, ![]() is the midpoint of
is the midpoint of ![]() , so
, so ![]() . Thus,
. Thus, ![]() . Therefore, our answer is
. Therefore, our answer is ![]() .
.
![]()
Video Solution by Mr. Math
https://www.youtube.com/watch?v=X_CSRwUh0Rc
See Also
| 2019 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()