Difference between revisions of "2003 AMC 8 Problems"
Math Kirby (talk | contribs) (→Problem 20) |
Superstriker (talk | contribs) (→Problem 12) |
||
| (46 intermediate revisions by 19 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{AMC8 Problems|year=2003|}} | ||
==Problem 1== | ==Problem 1== | ||
| − | Jamie counted the number of edges of a cube, Jimmy counted the numbers of corners, and Judy counted the number of faces. They then added the three numbers. What was the resulting sum? | + | Jamie counted the number of edges of a cube, Jimmy counted the numbers of corners, and Judy counted the number of faces. They then added the three numbers. What was the resulting sum? |
<math>\mathrm{(A)}\ 12 \qquad\mathrm{(B)}\ 16 \qquad\mathrm{(C)}\ 20 \qquad\mathrm{(D)}\ 22 \qquad\mathrm{(E)}\ 26</math> | <math>\mathrm{(A)}\ 12 \qquad\mathrm{(B)}\ 16 \qquad\mathrm{(C)}\ 20 \qquad\mathrm{(D)}\ 22 \qquad\mathrm{(E)}\ 26</math> | ||
| Line 14: | Line 15: | ||
==Problem 3== | ==Problem 3== | ||
| − | A burger at Ricky C's weighs | + | A burger at Ricky C's weighs 120 grams, of which 30 grams are filler. What percent of the burger is not filler? |
| − | What percent of the burger is not filler? | ||
<math>\mathrm{(A)}\ 60\% \qquad\mathrm{(B)}\ 65\% \qquad\mathrm{(C)}\ 70\% \qquad\mathrm{(D)}\ 75\% \qquad\mathrm{(E)}\ 90\%</math> | <math>\mathrm{(A)}\ 60\% \qquad\mathrm{(B)}\ 65\% \qquad\mathrm{(C)}\ 70\% \qquad\mathrm{(D)}\ 75\% \qquad\mathrm{(E)}\ 90\%</math> | ||
| Line 22: | Line 22: | ||
==Problem 4== | ==Problem 4== | ||
| − | A group of children riding on bicycles and tricycles rode past Billy Bob's house. Billy Bob counted | + | A group of children riding on bicycles and tricycles rode past Billy Bob's house. Billy Bob counted 7 children and 19 wheels. How many tricycles were there? |
<math>\mathrm{(A)}\ 2 \qquad\mathrm{(B)}\ 4 \qquad\mathrm{(C)}\ 5 \qquad\mathrm{(D)}\ 6 \qquad\mathrm{(E)}\ 7</math> | <math>\mathrm{(A)}\ 2 \qquad\mathrm{(B)}\ 4 \qquad\mathrm{(C)}\ 5 \qquad\mathrm{(D)}\ 6 \qquad\mathrm{(E)}\ 7</math> | ||
| Line 29: | Line 29: | ||
==Problem 5== | ==Problem 5== | ||
| − | If | + | If 20% of a number is 12, what is 30% of the same number? |
<math>\mathrm{(A)}\ 15\qquad\mathrm{(B)}\ 18 \qquad\mathrm{(C)}\ 20 \qquad\mathrm{(D)}\ 24 \qquad\mathrm{(E)}\ 30</math> | <math>\mathrm{(A)}\ 15\qquad\mathrm{(B)}\ 18 \qquad\mathrm{(C)}\ 20 \qquad\mathrm{(D)}\ 24 \qquad\mathrm{(E)}\ 30</math> | ||
| − | [[ | + | [[2003 AMC 8 Problems/Problem 5|Solution]] |
==Problem 6== | ==Problem 6== | ||
| − | Given the areas of the three squares in the figure, what is the area of the interior triangle? | + | Given the areas of the three squares in the figure, what is the area of the interior triangle? |
| + | |||
| + | <asy> | ||
| + | draw((0,0)--(-5,12)--(7,17)--(12,5)--(17,5)--(17,0)--(12,0)--(12,-12)--(0,-12)--(0,0)--(12,5)--(12,0)--cycle,linewidth(1)); | ||
| + | label("$25$",(14.5,1),N); | ||
| + | label("$144$",(6,-7.5),N); | ||
| + | label("$169$",(3.5,7),N); | ||
| + | </asy> | ||
<math>\mathrm{(A)}\ 13 \qquad\mathrm{(B)}\ 30 \qquad\mathrm{(C)}\ 60 \qquad\mathrm{(D)}\ 300 \qquad\mathrm{(E)}\ 1800</math> | <math>\mathrm{(A)}\ 13 \qquad\mathrm{(B)}\ 30 \qquad\mathrm{(C)}\ 60 \qquad\mathrm{(D)}\ 300 \qquad\mathrm{(E)}\ 1800</math> | ||
| Line 43: | Line 50: | ||
==Problem 7== | ==Problem 7== | ||
| − | Blake and Jenny each took four | + | Blake and Jenny each took four 100-point tests. Blake averaged 78 on the four tests. Jenny scored 10 points higher than Blake on the first test, 10 points lower than him on the second test, and 20 points higher on both the third and fourth tests. What is the difference between Jenny's average and Blake's average on these four tests? |
<math> \mathrm{(A)}\ 10 \qquad\mathrm{(B)}\ 15 \qquad\mathrm{(C)}\ 20 \qquad\mathrm{(D)}\ 25 \qquad\mathrm{(E)}\ 40 </math> | <math> \mathrm{(A)}\ 10 \qquad\mathrm{(B)}\ 15 \qquad\mathrm{(C)}\ 20 \qquad\mathrm{(D)}\ 25 \qquad\mathrm{(E)}\ 40 </math> | ||
| Line 49: | Line 56: | ||
[[2003 AMC 8 Problems/Problem 7|Solution]] | [[2003 AMC 8 Problems/Problem 7|Solution]] | ||
| − | ==Bake Sale | + | ==Problem 8== |
| − | Problems 8, 9 and 10 use the data found in the accompanying paragraph and figures | + | <math>\textbf{Bake Sale}</math> |
| + | |||
| + | (Problems 8, 9, and 10 use the data found in the accompanying paragraph and figures) | ||
Four friends, Art, Roger, Paul and Trisha, bake cookies, and all cookies have the same thickness. The shapes of the cookies differ, as shown. | Four friends, Art, Roger, Paul and Trisha, bake cookies, and all cookies have the same thickness. The shapes of the cookies differ, as shown. | ||
| − | <math>\circ</math> Art's cookies are trapezoids | + | <math>\circ</math> Art's cookies are trapezoids. |
| − | <asy>size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | + | <asy> |
| + | size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | ||
draw(origin--(5,0)--(5,3)--(2,3)--cycle); | draw(origin--(5,0)--(5,3)--(2,3)--cycle); | ||
draw(rightanglemark((5,3), (5,0), origin)); | draw(rightanglemark((5,3), (5,0), origin)); | ||
label("5 in", (2.5,0), S); | label("5 in", (2.5,0), S); | ||
label("3 in", (5,1.5), E); | label("3 in", (5,1.5), E); | ||
| − | label("3 in", (3.5,3), N);</asy> | + | label("3 in", (3.5,3), N); |
| + | </asy> | ||
| − | <math>\circ</math> Roger's cookies are rectangles | + | <math>\circ</math> Roger's cookies are rectangles. |
| − | <asy>size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | + | <asy> |
| + | size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | ||
draw(origin--(4,0)--(4,2)--(0,2)--cycle); | draw(origin--(4,0)--(4,2)--(0,2)--cycle); | ||
draw(rightanglemark((4,2), (4,0), origin)); | draw(rightanglemark((4,2), (4,0), origin)); | ||
draw(rightanglemark((0,2), origin, (4,0))); | draw(rightanglemark((0,2), origin, (4,0))); | ||
label("4 in", (2,0), S); | label("4 in", (2,0), S); | ||
| − | label("2 in", (4,1), E);</asy> | + | label("2 in", (4,1), E); |
| + | </asy> | ||
| − | <math>\circ</math> Paul's cookies are parallelograms | + | <math>\circ</math> Paul's cookies are parallelograms. |
| − | <asy>size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | + | <asy> |
| + | size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | ||
draw(origin--(3,0)--(2.5,2)--(-0.5,2)--cycle); | draw(origin--(3,0)--(2.5,2)--(-0.5,2)--cycle); | ||
draw((2.5,2)--(2.5,0), dashed); | draw((2.5,2)--(2.5,0), dashed); | ||
draw(rightanglemark((2.5,2),(2.5,0), origin)); | draw(rightanglemark((2.5,2),(2.5,0), origin)); | ||
label("3 in", (1.5,0), S); | label("3 in", (1.5,0), S); | ||
| − | label("2 in", (2.5,1), W);</asy> | + | label("2 in", (2.5,1), W); |
| + | </asy> | ||
| − | <math>\circ</math> Trisha's cookies are triangles | + | <math>\circ</math> Trisha's cookies are triangles. |
| − | <asy>size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | + | <asy> |
| + | size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); | ||
draw(origin--(3,0)--(3,4)--cycle); | draw(origin--(3,0)--(3,4)--cycle); | ||
draw(rightanglemark((3,4),(3,0), origin)); | draw(rightanglemark((3,4),(3,0), origin)); | ||
label("3 in", (1.5,0), S); | label("3 in", (1.5,0), S); | ||
| − | label("4 in", (3,2), E);</asy> | + | label("4 in", (3,2), E); |
| + | </asy> | ||
| − | + | Each friend uses the same amount of dough, and Art makes exactly 12 cookies. Who gets the fewest cookies from one batch of cookie dough? | |
| − | Who gets the fewest cookies from one batch of cookie dough? | ||
| − | <math> \textbf{(A)}\ \text{Art} \qquad\textbf{(B)}\ \text{ | + | <math> \textbf{(A)}\ \text{Art}\qquad\textbf{(B)}\ \text{Roger}\qquad\textbf{(C)}\ \text{Paul}\qquad\textbf{(D)}\ \text{Trisha}\qquad\textbf{(E)}\ \text{There is a tie for fewest.} </math> |
[[2003 AMC 8 Problems/Problem 8|Solution]] | [[2003 AMC 8 Problems/Problem 8|Solution]] | ||
| Line 107: | Line 123: | ||
==Problem 11== | ==Problem 11== | ||
| − | Business is a little slow at Lou's Fine Shoes, so Lou decides to have a | + | |
| − | sale. On Friday, Lou increases all of Thursday's prices by | + | Business is a little slow at Lou's Fine Shoes, so Lou decides to have a sale. On Friday, Lou increases all of Thursday's prices by 10%. Over the weekend, Lou advertises the sale: "Ten percent off the listed price. Sale starts Monday." How much does a pair of shoes cost on Monday that cost 40 dollars on Thursday? |
| − | weekend, Lou advertises the sale: Ten percent off the listed price. Sale | ||
| − | starts Monday." How much does a pair of shoes cost on Monday that | ||
| − | cost | ||
<math> \textbf{(A)}\ 36\qquad\textbf{(B)}\ 39.60\qquad\textbf{(C)}\ 40\qquad\textbf{(D)}\ 40.40\qquad\textbf{(E)}\ 44 </math> | <math> \textbf{(A)}\ 36\qquad\textbf{(B)}\ 39.60\qquad\textbf{(C)}\ 40\qquad\textbf{(D)}\ 40.40\qquad\textbf{(E)}\ 44 </math> | ||
| Line 118: | Line 131: | ||
==Problem 12== | ==Problem 12== | ||
| − | When a fair six-sided die is tossed on a table top, the bottom face cannot | + | |
| − | be seen. What is the probability that the product of the numbers on the | + | When a fair six-sided die is tossed on a table top, the bottom face cannot be seen. What is the probability that the product of the numbers on the five faces that can be seen is divisible by 6? |
| − | five faces that can be seen is divisible by 6? | ||
<math> \textbf{(A)}\ \frac{1}{3}\qquad\textbf{(B)}\ \frac{1}{2}\qquad\textbf{(C)}\ \frac{2}{3}\qquad\textbf{(D)}\ \frac{5}{6}\qquad\textbf{(E)}\ 1</math> | <math> \textbf{(A)}\ \frac{1}{3}\qquad\textbf{(B)}\ \frac{1}{2}\qquad\textbf{(C)}\ \frac{2}{3}\qquad\textbf{(D)}\ \frac{5}{6}\qquad\textbf{(E)}\ 1</math> | ||
| Line 127: | Line 139: | ||
==Problem 13== | ==Problem 13== | ||
| − | Fourteen white cubes are put together to form the | + | |
| + | Fourteen white cubes are put together to form the figure on the right. The complete surface of the figure, including the bottom, is painted red. The figure is then separated into individual cubes. How many of the individual cubes have exactly four red faces? | ||
<asy> | <asy> | ||
| Line 154: | Line 167: | ||
==Problem 14== | ==Problem 14== | ||
| + | |||
In this addition problem, each letter stands for a different digit. | In this addition problem, each letter stands for a different digit. | ||
| − | <math> \setlength{\tabcolsep}{0.5mm}\begin{array}{cccc}&T & W & O\ | + | <math> \setlength{\tabcolsep}{0.5mm}\begin{array}{cccc}&T & W & O\ + &T & W & O\ \hline F& O & U & R\end{array} </math> |
| − | If T = 7 and the letter O represents an even number, what is the only possible value for W? | + | If <math>T = 7</math> and the letter <math>O</math> represents an even number, what is the only possible value for <math>W</math>? |
| − | <math>\textbf{(A)}\ 0 \qquad | + | <math>\textbf{(A)}\ 0 \qquad \textbf{(B)}\ 1 \qquad \textbf{(C)}\ 2\qquad \textbf{(D)}\ 3\qquad \textbf{(E)}\ 4</math> |
| − | \textbf{(B)}\ 1 \qquad | ||
| − | \textbf{(C)}\ 2\qquad | ||
| − | \textbf{(D)}\ 3\qquad | ||
| − | \textbf{(E)}\ 4</math> | ||
[[2003 AMC 8 Problems/Problem 14|Solution]] | [[2003 AMC 8 Problems/Problem 14|Solution]] | ||
==Problem 15== | ==Problem 15== | ||
| + | |||
A figure is constructed from unit cubes. Each cube shares at least one face with another cube. What is the minimum number of cubes needed to build a figure with the front and side views shown? | A figure is constructed from unit cubes. Each cube shares at least one face with another cube. What is the minimum number of cubes needed to build a figure with the front and side views shown? | ||
| Line 184: | Line 195: | ||
==Problem 16== | ==Problem 16== | ||
| − | |||
| − | <math>\textbf{(A)}\ 2 \qquad | + | Ali, Bonnie, Carlo, and Dianna are going to drive together to a nearby theme park. The car they are using has 4 seats: 1 driver's seat, 1 front passenger seat, and 2 back passenger seats. Bonnie and Carlo are the only ones who know how to drive the car. How many possible seating arrangements are there? |
| − | \textbf{(B)}\ 4 \qquad | + | |
| − | \textbf{(C)}\ 6 \qquad | + | <math>\textbf{(A)}\ 2 \qquad \textbf{(B)}\ 4 \qquad \textbf{(C)}\ 6 \qquad \textbf{(D)}\ 12 \qquad \textbf{(E)}\ 24</math> |
| − | \textbf{(D)}\ 12 \qquad | ||
| − | \textbf{(E)}\ 24</math> | ||
[[2003 AMC 8 Problems/Problem 16|Solution]] | [[2003 AMC 8 Problems/Problem 16|Solution]] | ||
==Problem 17== | ==Problem 17== | ||
| + | |||
The six children listed below are from two families of three siblings each. Each child has blue or brown eyes and black or blond hair. Children from the same family have at least one of these characteristics in common. Which two children are Jim's siblings? | The six children listed below are from two families of three siblings each. Each child has blue or brown eyes and black or blond hair. Children from the same family have at least one of these characteristics in common. Which two children are Jim's siblings? | ||
| + | |||
<cmath> | <cmath> | ||
| − | <math> \textbf{(A)}\ \text{Nadeen and Austin}\qquad\textbf{(B)}\ \text{Benjamin and Sue}\qquad\textbf{(C)}\ \text{Benjamin and Austin}\qquad\textbf{(D)}\ \text{Nadeen and Tevyn} | + | |
| − | <math> \textbf{(E)}\ \text{Austin and Sue} </math> | + | <math>\textbf{(A)}\ \text{Nadeen and Austin}\qquad\textbf{(B)}\ \text{Benjamin and Sue}\qquad\textbf{(C)}\ \text{Benjamin and Austin}\qquad\textbf{(D)}\ \text{Nadeen and Tevyn}</math> |
| + | |||
| + | <math>\textbf{(E)}\ \text{Austin and Sue} </math> | ||
[[2003 AMC 8 Problems/Problem 17|Solution]] | [[2003 AMC 8 Problems/Problem 17|Solution]] | ||
==Problem 18== | ==Problem 18== | ||
| + | |||
Each of the twenty dots on the graph below represents one of Sarah's classmates. Classmates who are friends are connected with a line segment. For her birthday party, Sarah is inviting only the following: all of her friends and all of those classmates who are friends with at least one of her friends. How many classmates will not be invited to Sarah's party? | Each of the twenty dots on the graph below represents one of Sarah's classmates. Classmates who are friends are connected with a line segment. For her birthday party, Sarah is inviting only the following: all of her friends and all of those classmates who are friends with at least one of her friends. How many classmates will not be invited to Sarah's party? | ||
<asy>/* AMC8 2003 #18 Problem */ | <asy>/* AMC8 2003 #18 Problem */ | ||
| Line 232: | Line 245: | ||
==Problem 19== | ==Problem 19== | ||
| − | |||
| − | <math>\textbf{(A)}\ 1 \qquad | + | How many integers between 1000 and 2000 have all three of the numbers 15, 20, and 25 as factors? |
| − | \textbf{(B)}\ 2 \qquad | + | |
| − | \textbf{(C)}\ 3 \qquad | + | <math>\textbf{(A)}\ 1 \qquad \textbf{(B)}\ 2 \qquad \textbf{(C)}\ 3 \qquad \textbf{(D)}\ 4 \qquad \textbf{(E)}\ 5</math> |
| − | \textbf{(D)}\ 4 \qquad | ||
| − | \textbf{(E)}\ 5</math> | ||
[[2003 AMC 8 Problems/Problem 19|Solution]] | [[2003 AMC 8 Problems/Problem 19|Solution]] | ||
==Problem 20== | ==Problem 20== | ||
| − | |||
| − | <math>\textbf{(A)}\ 0 \qquad | + | What is the measure of the acute angle formed by the hands of the clock at 4:20 PM? |
| − | \textbf{(B)}\ 5 \qquad | + | |
| − | \textbf{(C)}\ 8 \qquad | + | <math>\textbf{(A)}\ 0 \qquad \textbf{(B)}\ 5 \qquad \textbf{(C)}\ 8 \qquad \textbf{(D)}\ 10 \qquad \textbf{(E)}\ 12</math> |
| − | \textbf{(D)}\ 10 \qquad | ||
| − | \textbf{(E)}\ 12</math> | ||
[[2003 AMC 8 Problems/Problem 20|Solution]] | [[2003 AMC 8 Problems/Problem 20|Solution]] | ||
==Problem 21== | ==Problem 21== | ||
| − | The area of trapezoid <math> ABCD</math> is <math> 164 \text{cm}^2</math>. The altitude is | + | |
| + | The area of trapezoid <math> ABCD</math> is <math>164\text{ cm}^2</math>. The altitude is 8 cm, <math>AB</math> is 10 cm, and <math>CD</math> is 17 cm. What is <math>BC</math>, in centimeters? | ||
| + | |||
<asy>/* AMC8 2003 #21 Problem */ | <asy>/* AMC8 2003 #21 Problem */ | ||
size(4inch,2inch); | size(4inch,2inch); | ||
| Line 269: | Line 278: | ||
<math> \textbf{(A)}\ 9\qquad\textbf{(B)}\ 10\qquad\textbf{(C)}\ 12\qquad\textbf{(D)}\ 15\qquad\textbf{(E)}\ 20</math> | <math> \textbf{(A)}\ 9\qquad\textbf{(B)}\ 10\qquad\textbf{(C)}\ 12\qquad\textbf{(D)}\ 15\qquad\textbf{(E)}\ 20</math> | ||
| + | |||
| + | [[2003 AMC 8 Problems/Problem 21|Solution]] | ||
==Problem 22== | ==Problem 22== | ||
| Line 304: | Line 315: | ||
<math> \textbf{(A)}\ \text{A only}\qquad\textbf{(B)}\ \text{B only}\qquad\textbf{(C)}\ \text{C only}\qquad\textbf{(D)}\ \text{both A and B}\qquad\textbf{(E)}\ \text{all are equal}</math> | <math> \textbf{(A)}\ \text{A only}\qquad\textbf{(B)}\ \text{B only}\qquad\textbf{(C)}\ \text{C only}\qquad\textbf{(D)}\ \text{both A and B}\qquad\textbf{(E)}\ \text{all are equal}</math> | ||
| + | |||
| + | [[2003 AMC 8 Problems/Problem 22|Solution]] | ||
==Problem 23== | ==Problem 23== | ||
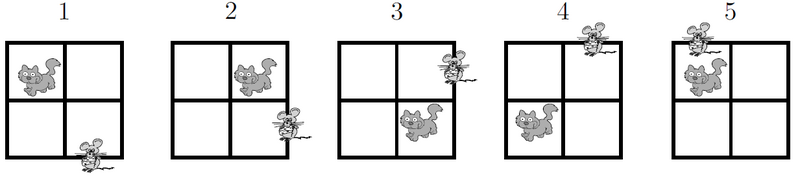
| − | In the pattern below, the cat | + | In the pattern below, the cat moves clockwise through the four squares and the mouse moves counterclockwise through the eight exterior segments of the four squares. |
| − | < | + | <center> |
| − | + | [[Image:2003amc8prob23a.png|800px]] | |
| − | + | </center> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
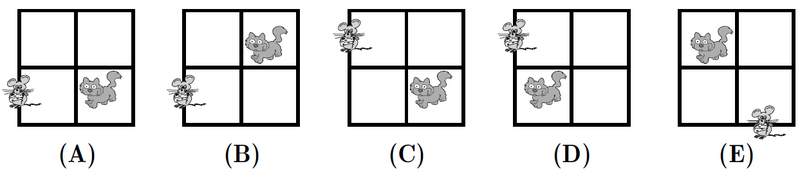
If the pattern is continued, where would the cat and mouse be after the 247th move? | If the pattern is continued, where would the cat and mouse be after the 247th move? | ||
| − | < | + | <center> |
| − | + | [[Image:2003amc8prob23b.png|800px]] | |
| − | + | </center> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | [[2003 AMC 8 Problems/Problem 23|Solution]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Problem 24== | ==Problem 24== | ||
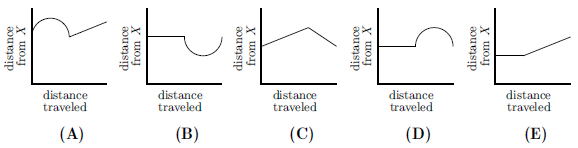
| − | A ship travels from point A to point B along a semicircular path, centered at Island X. Then it travels along a straight path from B to C. Which of these graphs best shows the ship's distance from Island X as it moves along its course? | + | A ship travels from point <math>A</math> to point <math>B</math> along a semicircular path, centered at Island <math>X</math>. Then it travels along a straight path from <math>B</math> to <math>C</math>. Which of these graphs best shows the ship's distance from Island <math>X</math> as it moves along its course? |
<asy>size(150); | <asy>size(150); | ||
| Line 393: | Line 343: | ||
label("$C$", C, N); | label("$C$", C, N); | ||
label("$B$", B, E); | label("$B$", B, E); | ||
| − | label("$A$", A, W | + | label("$A$", A, W); |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</asy> | </asy> | ||
| − | < | + | <center> |
| − | + | [[Image:2003amc8prob24ans.png|800px]] | |
| − | + | </center> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | [[2003 AMC 8 Problems/Problem 24|Solution]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Problem 25== | ==Problem 25== | ||
| − | In the figure, the area of square WXYZ is <math>25 \text{cm}^2</math>. The four smaller squares have sides 1 cm long, either parallel to or coinciding with the sides of the large square. In <math>\ | + | In the figure, the area of square <math>WXYZ</math> is <math>25 \text{ cm}^2</math>. The four smaller squares have sides 1 cm long, either parallel to or coinciding with the sides of the large square. In <math>\triangle ABC</math>, <math>AB = AC</math>, and when <math>\triangle ABC</math> is folded over side <math>\overline{BC}</math>, point <math>A</math> coincides with <math>O</math>, the center of square <math>WXYZ</math>. What is the area of <math>\triangle ABC</math>, in square centimeters? |
<asy> | <asy> | ||
| Line 461: | Line 368: | ||
label("$W$",W , NE); | label("$W$",W , NE); | ||
label("$X$", X, N); | label("$X$", X, N); | ||
| − | label("$Y$", Y, | + | label("$Y$", Y, S); |
label("$Z$", Z, SE); | label("$Z$", Z, SE); | ||
</asy> | </asy> | ||
<math> \textbf{(A)}\ \frac{15}4\qquad\textbf{(B)}\ \frac{21}4\qquad\textbf{(C)}\ \frac{27}4\qquad\textbf{(D)}\ \frac{21}2\qquad\textbf{(E)}\ \frac{27}2</math> | <math> \textbf{(A)}\ \frac{15}4\qquad\textbf{(B)}\ \frac{21}4\qquad\textbf{(C)}\ \frac{27}4\qquad\textbf{(D)}\ \frac{21}2\qquad\textbf{(E)}\ \frac{27}2</math> | ||
| + | |||
| + | [[2003 AMC 8 Problems/Problem 25|Solution]] | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC8 box|year=2003|before=[[2002 AMC 8 Problems|2002 AMC 8]]|after=[[2004 AMC 8 Problems|2004 AMC 8]]}} | ||
| + | * [[AMC 8]] | ||
| + | * [[AMC 8 Problems and Solutions]] | ||
| + | * [[Mathematics competition resources]] | ||
| + | |||
| + | |||
| + | {{MAA Notice}} | ||
Latest revision as of 12:02, 19 February 2024
| 2003 AMC 8 (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See Also
Problem 1
Jamie counted the number of edges of a cube, Jimmy counted the numbers of corners, and Judy counted the number of faces. They then added the three numbers. What was the resulting sum?
![]()
Problem 2
Which of the following numbers has the smallest prime factor?
![]()
Problem 3
A burger at Ricky C's weighs 120 grams, of which 30 grams are filler. What percent of the burger is not filler?
![]()
Problem 4
A group of children riding on bicycles and tricycles rode past Billy Bob's house. Billy Bob counted 7 children and 19 wheels. How many tricycles were there?
![]()
Problem 5
If 20% of a number is 12, what is 30% of the same number?
![]()
Problem 6
Given the areas of the three squares in the figure, what is the area of the interior triangle?
![[asy] draw((0,0)--(-5,12)--(7,17)--(12,5)--(17,5)--(17,0)--(12,0)--(12,-12)--(0,-12)--(0,0)--(12,5)--(12,0)--cycle,linewidth(1)); label("$25$",(14.5,1),N); label("$144$",(6,-7.5),N); label("$169$",(3.5,7),N); [/asy]](http://latex.artofproblemsolving.com/3/7/2/372ee1f13836b7ad774c0aa23e598d4f8b07cbb6.png)
![]()
Problem 7
Blake and Jenny each took four 100-point tests. Blake averaged 78 on the four tests. Jenny scored 10 points higher than Blake on the first test, 10 points lower than him on the second test, and 20 points higher on both the third and fourth tests. What is the difference between Jenny's average and Blake's average on these four tests?
![]()
Problem 8
![]()
(Problems 8, 9, and 10 use the data found in the accompanying paragraph and figures)
Four friends, Art, Roger, Paul and Trisha, bake cookies, and all cookies have the same thickness. The shapes of the cookies differ, as shown.
![]() Art's cookies are trapezoids.
Art's cookies are trapezoids.
![[asy] size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); draw(origin--(5,0)--(5,3)--(2,3)--cycle); draw(rightanglemark((5,3), (5,0), origin)); label("5 in", (2.5,0), S); label("3 in", (5,1.5), E); label("3 in", (3.5,3), N); [/asy]](http://latex.artofproblemsolving.com/3/d/5/3d531b95a6e97cf02b7ade98fe9eebdcf1a10ad3.png)
![]() Roger's cookies are rectangles.
Roger's cookies are rectangles.
![[asy] size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); draw(origin--(4,0)--(4,2)--(0,2)--cycle); draw(rightanglemark((4,2), (4,0), origin)); draw(rightanglemark((0,2), origin, (4,0))); label("4 in", (2,0), S); label("2 in", (4,1), E); [/asy]](http://latex.artofproblemsolving.com/3/b/b/3bb42c95ed47ad88dc8045d2158c24b3b513dc36.png)
![]() Paul's cookies are parallelograms.
Paul's cookies are parallelograms.
![[asy] size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); draw(origin--(3,0)--(2.5,2)--(-0.5,2)--cycle); draw((2.5,2)--(2.5,0), dashed); draw(rightanglemark((2.5,2),(2.5,0), origin)); label("3 in", (1.5,0), S); label("2 in", (2.5,1), W); [/asy]](http://latex.artofproblemsolving.com/0/f/f/0ff4ffd66b62485d742d63d1b12a9a321024937a.png)
![]() Trisha's cookies are triangles.
Trisha's cookies are triangles.
![[asy] size(80);defaultpen(linewidth(0.8));defaultpen(fontsize(8)); draw(origin--(3,0)--(3,4)--cycle); draw(rightanglemark((3,4),(3,0), origin)); label("3 in", (1.5,0), S); label("4 in", (3,2), E); [/asy]](http://latex.artofproblemsolving.com/5/b/7/5b7f1b1605342590d1d41eae41b1be7f1ebbf9a5.png)
Each friend uses the same amount of dough, and Art makes exactly 12 cookies. Who gets the fewest cookies from one batch of cookie dough?
![]()
Problem 9
Each friend uses the same amount of dough, and Art makes exactly ![]() cookies. Art's cookies sell for
cookies. Art's cookies sell for ![]() cents each. To earn the same amount from a single batch, how much should one of Roger's cookies cost in cents?
cents each. To earn the same amount from a single batch, how much should one of Roger's cookies cost in cents?
![]()
Problem 10
How many cookies will be in one batch of Trisha's cookies?
![]()
Problem 11
Business is a little slow at Lou's Fine Shoes, so Lou decides to have a sale. On Friday, Lou increases all of Thursday's prices by 10%. Over the weekend, Lou advertises the sale: "Ten percent off the listed price. Sale starts Monday." How much does a pair of shoes cost on Monday that cost 40 dollars on Thursday?
![]()
Problem 12
When a fair six-sided die is tossed on a table top, the bottom face cannot be seen. What is the probability that the product of the numbers on the five faces that can be seen is divisible by 6?
![]()
Problem 13
Fourteen white cubes are put together to form the figure on the right. The complete surface of the figure, including the bottom, is painted red. The figure is then separated into individual cubes. How many of the individual cubes have exactly four red faces?
![[asy] import three; defaultpen(linewidth(0.8)); real r=0.5; currentprojection=orthographic(3/4,8/15,7/15); draw(unitcube, white, thick(), nolight); draw(shift(1,0,0)*unitcube, white, thick(), nolight); draw(shift(2,0,0)*unitcube, white, thick(), nolight); draw(shift(0,0,1)*unitcube, white, thick(), nolight); draw(shift(2,0,1)*unitcube, white, thick(), nolight); draw(shift(0,1,0)*unitcube, white, thick(), nolight); draw(shift(2,1,0)*unitcube, white, thick(), nolight); draw(shift(0,2,0)*unitcube, white, thick(), nolight); draw(shift(2,2,0)*unitcube, white, thick(), nolight); draw(shift(0,3,0)*unitcube, white, thick(), nolight); draw(shift(0,3,1)*unitcube, white, thick(), nolight); draw(shift(1,3,0)*unitcube, white, thick(), nolight); draw(shift(2,3,0)*unitcube, white, thick(), nolight); draw(shift(2,3,1)*unitcube, white, thick(), nolight);[/asy]](http://latex.artofproblemsolving.com/e/c/4/ec490b94b3cc33cceee6968204269eb392d87c3d.png)
![]()
Problem 14
In this addition problem, each letter stands for a different digit.

If ![]() and the letter
and the letter ![]() represents an even number, what is the only possible value for
represents an even number, what is the only possible value for ![]() ?
?
![]()
Problem 15
A figure is constructed from unit cubes. Each cube shares at least one face with another cube. What is the minimum number of cubes needed to build a figure with the front and side views shown?
![[asy] defaultpen(linewidth(0.8)); path p=unitsquare; draw(p^^shift(0,1)*p^^shift(1,0)*p); draw(shift(4,0)*p^^shift(5,0)*p^^shift(5,1)*p); label("FRONT", (1,0), S); label("SIDE", (5,0), S);[/asy]](http://latex.artofproblemsolving.com/9/0/9/909c990102c2e104c145a3c91e964d4e1e22c59a.png)
![]()
Problem 16
Ali, Bonnie, Carlo, and Dianna are going to drive together to a nearby theme park. The car they are using has 4 seats: 1 driver's seat, 1 front passenger seat, and 2 back passenger seats. Bonnie and Carlo are the only ones who know how to drive the car. How many possible seating arrangements are there?
![]()
Problem 17
The six children listed below are from two families of three siblings each. Each child has blue or brown eyes and black or blond hair. Children from the same family have at least one of these characteristics in common. Which two children are Jim's siblings?
![\[\begin{array}{c|c|c}\text{Child}&\text{Eye Color}&\text{Hair Color}\\ \hline\text{Benjamin}&\text{Blue}&\text{Black}\\ \hline\text{Jim}&\text{Brown}&\text{Blonde}\\ \hline\text{Nadeen}&\text{Brown}&\text{Black}\\ \hline\text{Austin}&\text{Blue}&\text{Blonde}\\ \hline\text{Tevyn}&\text{Blue}&\text{Black}\\ \hline\text{Sue}&\text{Blue}&\text{Blonde}\\ \hline\end{array}\]](http://latex.artofproblemsolving.com/0/a/e/0ae4f05da3c8e0d429452248f1039b98196d0c98.png)
![]()
![]()
Problem 18
Each of the twenty dots on the graph below represents one of Sarah's classmates. Classmates who are friends are connected with a line segment. For her birthday party, Sarah is inviting only the following: all of her friends and all of those classmates who are friends with at least one of her friends. How many classmates will not be invited to Sarah's party?
![[asy]/* AMC8 2003 #18 Problem */ pair a=(102,256), b=(68,131), c=(162,101), d=(134,150); pair e=(269,105), f=(359,104), g=(303,12), h=(579,211); pair i=(534, 342), j=(442,432), k=(374,484), l=(278,501); pair m=(282,411), n=(147,451), o=(103,437), p=(31,373); pair q=(419,175), r=(462,209), s=(477,288), t=(443,358); pair oval=(282,303); draw(l--m--n--cycle); draw(p--oval); draw(o--oval); draw(b--d--oval); draw(c--d--e--oval); draw(e--f--g--h--i--j--oval); draw(k--oval); draw(q--oval); draw(s--oval); draw(r--s--t--oval); dot(a); dot(b); dot(c); dot(d); dot(e); dot(f); dot(g); dot(h); dot(i); dot(j); dot(k); dot(l); dot(m); dot(n); dot(o); dot(p); dot(q); dot(r); dot(s); dot(t); filldraw(yscale(.5)*Circle((282,606),80),white,black); label(scale(0.75)*"Sarah", oval);[/asy]](http://latex.artofproblemsolving.com/8/5/7/8574a9ed5e1d1bbfa8860c587504b3d9136789cd.png)
![]()
Problem 19
How many integers between 1000 and 2000 have all three of the numbers 15, 20, and 25 as factors?
![]()
Problem 20
What is the measure of the acute angle formed by the hands of the clock at 4:20 PM?
![]()
Problem 21
The area of trapezoid ![]() is
is ![]() . The altitude is 8 cm,
. The altitude is 8 cm, ![]() is 10 cm, and
is 10 cm, and ![]() is 17 cm. What is
is 17 cm. What is ![]() , in centimeters?
, in centimeters?
![[asy]/* AMC8 2003 #21 Problem */ size(4inch,2inch); draw((0,0)--(31,0)--(16,8)--(6,8)--cycle); draw((11,8)--(11,0), linetype("8 4")); draw((11,1)--(12,1)--(12,0)); label("$A$", (0,0), SW); label("$D$", (31,0), SE); label("$B$", (6,8), NW); label("$C$", (16,8), NE); label("10", (3,5), W); label("8", (11,4), E); label("17", (22.5,5), E);[/asy]](http://latex.artofproblemsolving.com/c/6/6/c66899b4bcfdeca2247f2e6ca1ab430486b95306.png)
![]()
Problem 22
The following figures are composed of squares and circles. Which figure has a shaded region with largest area?
![[asy]/* AMC8 2003 #22 Problem */ size(3inch, 2inch); unitsize(1cm); pen outline = black+linewidth(1); filldraw((0,0)--(2,0)--(2,2)--(0,2)--cycle, mediumgrey, outline); filldraw(shift(3,0)*((0,0)--(2,0)--(2,2)--(0,2)--cycle), mediumgrey, outline); filldraw(Circle((7,1), 1), mediumgrey, black+linewidth(1)); filldraw(Circle((1,1), 1), white, outline); filldraw(Circle((3.5,.5), .5), white, outline); filldraw(Circle((4.5,.5), .5), white, outline); filldraw(Circle((3.5,1.5), .5), white, outline); filldraw(Circle((4.5,1.5), .5), white, outline); filldraw((6.3,.3)--(7.7,.3)--(7.7,1.7)--(6.3,1.7)--cycle, white, outline); label("A", (1, 2), N); label("B", (4, 2), N); label("C", (7, 2), N); draw((0,-.5)--(.5,-.5), BeginArrow); draw((1.5, -.5)--(2, -.5), EndArrow); label("2 cm", (1, -.5)); draw((3,-.5)--(3.5,-.5), BeginArrow); draw((4.5, -.5)--(5, -.5), EndArrow); label("2 cm", (4, -.5)); draw((6,-.5)--(6.5,-.5), BeginArrow); draw((7.5, -.5)--(8, -.5), EndArrow); label("2 cm", (7, -.5)); draw((6,1)--(6,-.5), linetype("4 4")); draw((8,1)--(8,-.5), linetype("4 4"));[/asy]](http://latex.artofproblemsolving.com/6/6/6/666ac41befa9511afaf3ff9277993a8e313ccc43.png)
![]()
Problem 23
In the pattern below, the cat moves clockwise through the four squares and the mouse moves counterclockwise through the eight exterior segments of the four squares.
If the pattern is continued, where would the cat and mouse be after the 247th move?
Problem 24
A ship travels from point ![]() to point
to point ![]() along a semicircular path, centered at Island
along a semicircular path, centered at Island ![]() . Then it travels along a straight path from
. Then it travels along a straight path from ![]() to
to ![]() . Which of these graphs best shows the ship's distance from Island
. Which of these graphs best shows the ship's distance from Island ![]() as it moves along its course?
as it moves along its course?
![[asy]size(150); pair X=origin, A=(-5,0), B=(5,0), C=(0,5); draw(Arc(X, 5, 180, 360)^^B--C); dot(X); label("$X$", X, NE); label("$C$", C, N); label("$B$", B, E); label("$A$", A, W); [/asy]](http://latex.artofproblemsolving.com/9/1/9/91933f8be27c24174af480d964c31782da9f3bb4.png)
Problem 25
In the figure, the area of square ![]() is
is ![]() . The four smaller squares have sides 1 cm long, either parallel to or coinciding with the sides of the large square. In
. The four smaller squares have sides 1 cm long, either parallel to or coinciding with the sides of the large square. In ![]() ,
, ![]() , and when
, and when ![]() is folded over side
is folded over side ![]() , point
, point ![]() coincides with
coincides with ![]() , the center of square
, the center of square ![]() . What is the area of
. What is the area of ![]() , in square centimeters?
, in square centimeters?
![[asy] defaultpen(fontsize(8)); size(225); pair Z=origin, W=(0,10), X=(10,10), Y=(10,0), O=(5,5), B=(-4,8), C=(-4,2), A=(-13,5); draw((-4,0)--Y--X--(-4,10)--cycle); draw((0,-2)--(0,12)--(-2,12)--(-2,8)--B--A--C--(-2,2)--(-2,-2)--cycle); dot(O); label("$A$", A, NW); label("$O$", O, NE); label("$B$", B, SW); label("$C$", C, NW); label("$W$",W , NE); label("$X$", X, N); label("$Y$", Y, S); label("$Z$", Z, SE); [/asy]](http://latex.artofproblemsolving.com/f/b/5/fb5de36e57bfb81488edf36e2717cf7b93f0444b.png)
![]()
See Also
| 2003 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by 2002 AMC 8 |
Followed by 2004 AMC 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()