Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AMC 10A Problems/Problem 22"

(Blanked the page)
(Tag: Blanking)
(→‎Solution 3)
 
(92 intermediate revisions by 22 users not shown)
Line 1: Line 1:
 +
==Problem==
 +
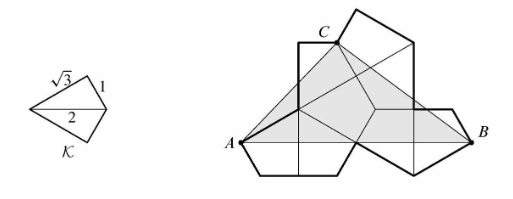
Let <math>\mathcal K</math> be the kite formed by joining two right triangles with legs <math>1</math> and <math>\sqrt3</math> along a common hypotenuse. Eight copies of <math>\mathcal K</math> are used to form the polygon shown below. What is the area of triangle <math>\Delta ABC</math>?
  
 +
[[File:Asset-ddfea426a1acee64ea44467d8aa8797a.png]]
 +
 +
<math>\textbf{(A) }2+3\sqrt3\qquad\textbf{(B) }\dfrac92\sqrt3\qquad\textbf{(C) }\dfrac{10+8\sqrt3}{3}\qquad\textbf{(D) }8\qquad\textbf{(E) }5\sqrt3</math>
 +
 +
==Solution 1==
 +
 +
[[File:2024 AMC 10 A Diagram Problem 22.png]]
 +
 +
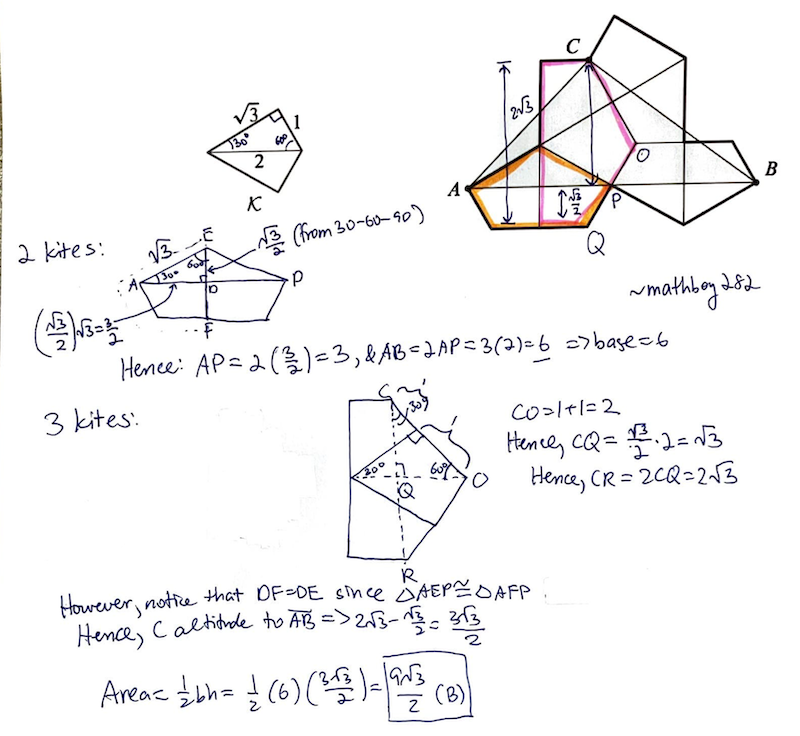
First, we should find the length of <math>AB</math>. In order to do this, as we see in the diagram, it can be split into 4 equal sections. Since diagram <math>K</math> shows us that it is made up of two <math>{30,60,90}</math> triangles, then the triangle outlined in red must be a <math>30,60,90</math> triangle, as <math>{30+30=60}</math>, and the two lines are perpendicular (it is proveable, but during competition, it is best to assume this is true, as the diagram is draw pretty well to scale). Also, since we know the length of the longest side of the red triangle is <math>{\sqrt3}</math>, then the side we are looking for, which is outlined in blue, must be <math>\frac{3}{2}</math> by the <math>{1,\sqrt3, 2}</math> relationship of <math>{30,60,90}</math> triangles. Therefore <math>AB</math>, which is the base of the triangle we are looking, for must be <math>6.</math>
 +
 +
 +
Now all we have to do is find the height. We can split the height into 2 sections, the green and the light green. The green section must be <math>{\sqrt3}</math>, as <math>K</math> shows us. Also, the light green section must be equal to <math>{\frac{\sqrt3}{2}}</math>, as in the previous paragraph, the triangle outlined in red is <math>30,60,90</math>. Then, the green section, which is the height, must be <math>{\sqrt3}+{\frac{\sqrt3}{2}}</math>, which is just <math>{\frac{3\sqrt3}{2}}</math>.
 +
 +
 +
Then the area of the triangle must be <math>{\frac{1}{2}}\cdot {b} \cdot {h}</math>, which is just <math>\boxed{  \textbf{(B) } \frac{9}{2} \sqrt3}.</math>
 +
 +
~Solution by [[User:HappySharks|HappySharks]]
 +
~Minor Edits by [[User:Mathkiddus|mathkiddus]]
 +
 +
==Solution 2==
 +
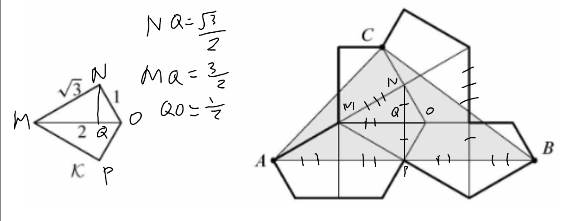
Let <math>\mathcal K</math> be quadrilateral <math>MNOP</math>. Drawing line <math>MO</math> splits the triangle into <math>\Delta MNO</math>.
 +
Drawing the altitude from <math>N</math> to point <math>Q</math> on line <math>MO</math>, we know <math>NQ</math> is <math>\frac{\sqrt{3}}{2}</math>, <math>MQ</math> is <math>\frac{3}{2}</math>, and <math>QO</math> is <math>\frac{1}{2}</math>.
 +
 +
[[File:Screenshot 2024-11-08 2.33.52 PM.png]]
 +
 +
Due to the many similarities present, we can find that <math>AB</math> is <math>4(MQ)</math>, and the height of <math>\Delta ABC</math> is <math>NQ+MN</math>
 +
 +
<math>AB</math> is <math>4(\frac{3}{2})=6</math> and the height of <math>\Delta ABC</math> is <math>\sqrt3+\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}</math>.
 +
 +
Solving for the area of <math>\Delta ABC</math> gives <math>6\cdot\frac{3\sqrt{3}}{2}\cdot\frac{1}{2}</math> which is <math>\boxed{\textbf{(B) }\dfrac92\sqrt3}</math>
 +
 +
~9897 (latex beginner here)
 +
 +
~i_am_suk_at_math(very minor latex edits)
 +
 +
==Solution 3==
 +
 +
Let's start by looking at kite <math>\mathcal K</math>. We can quickly deduce based off of the side lengths that the kite can be split into two <math>30-60-90</math> triangles. Going back to the triangle <math>\triangle ABC</math>, focus on side <math>AB</math>. There are <math>4</math> kites, they are all either reflected over the line <math>AB</math> or a line perpendicular to <math>AB</math>, meaning the length of <math>AB</math> can be split up into 4 equal parts.
 +
 +
Pick out the bottom-left kite, and we can observe that the kite and the triangle formed by the intersection of the kite and <math>\Delta ABC</math> share a <math>60</math> degree angle. (this was deduced from the <math>30-60-90</math> triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a <math>90^{\circ}</math> angle. Because that is also a <math>30-60-90</math> triangle with a hypotenuse of <math>\sqrt3</math>, so we find the length of AB to be <math>4*3/2</math>, which is <math>6</math>.
 +
 +
Then, we can drop an altitude from <math>C</math> to <math>AB</math>. We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and <math>\Delta ABC</math>. (Look at the line formed on the left of <math>C</math> that drops down to <math>AB</math> if you are confused) We already have those values from the <math>30-60-90</math> triangles, so we can just plug it into the triangle area formula, <math>bh/2</math>. We get <cmath>6\cdot\dfrac{\sqrt3+\frac{\sqrt3}{2}}{2}\rightarrow3\cdot(\sqrt3+\dfrac{\sqrt3}{2})\rightarrow3\cdot\dfrac{\sqrt3}{2}\rightarrow\boxed{\textbf{(B) }\dfrac92\sqrt3}</cmath>
 +
 +
~YTH
 +
 +
~WIP (Header)
 +
 +
~Tacos_are_yummy_1 (<math>\LaTeX</math> & Formatting)
 +
 +
==Solution 4==
 +
 +
[[File:202410A_23v2.png]]
 +
 +
~mathboy282
 +
 +
==Solution 5 ==
 +
Let the point of intersection of <math>AB</math> and the kite with <math>A</math> as vertex be <math>D</math>.
 +
 +
Let the left kite with <math>C</math> as a vertex touch the kite with <math>A</math> as vertex at point <math>E</math>.
 +
 +
<math>\triangle ADE</math> is a <math>30-60-90</math> so <math>AD = \frac{3}{2}</math> and <math>DE = \frac{\sqrt3}{2}</math>.
 +
 +
So, <math>AB = 4\cdot AD = 6</math> and <math>CD=CE+DE= \frac{3\sqrt3}{2}</math>, and the area is <math>\frac12\cdot AB \cdot CD = \boxed{  \textbf{(B) } \frac{9}{2} \sqrt3}.</math>
 +
 +
~Mintylemon66
 +
==Solution 6(trig bash)==
 +
[[File:Screenshot_2024-11-09_201440.png]]
 +
<cmath>\textbf{Step 1:} </cmath>
 +
As stated in the solutions above we can easily find that <math>AB</math> is split into <math>4</math> equal parts, so we have <math>AB=4(AE)</math> We can calculate <math>AE,</math> by using <math>AA</math> similarity to find <math>\triangle{ADE}</math> is a <math>30-60-90</math> triangle, therefore we have <math>AD=\sqrt{3},DE=\frac{\sqrt{3}}{2},</math> and finally <math>AE=\frac{3}{2},</math> therefore <math>AB=4(AE)=4(\frac{3}{2})=6.</math> Similarly we have <math>CF</math> is congruent to <math>FG,</math> therefore <math>CF=FG=1.</math> Next we have <math>AD</math> is congruent to <math>DF</math> telling us <math>AF=AD+DF=2(AD)=2\sqrt{3}.</math> Noticing <math>\triangle{CFA}</math> is right, we apply Pythagorean theorem to <math>\triangle{CFA}</math> to find
 +
<cmath>AC^2=CF^2+AF^2</cmath>
 +
<cmath>AC^2=(1)^2+(2\sqrt{3})^2=13</cmath>
 +
<cmath>AC=\sqrt{13}.</cmath>
 +
<cmath>\textbf{Step 2:} </cmath>
 +
Next we would like to calculate CJ, As said before <math>CF=FG=1</math> so <math>CG=2.</math> We know the inscribed angle between CG and GJ is <math>60\cdot2=120,</math> and finally we know <math>GJ=1.</math> So we apply LoC on triangle CGJ in order to find CJ.
 +
<cmath>CJ^2=CG^2+GJ^2-2\cdot{CG}\cdot{GJ}\cdot\cos{120^{\circ}}. </cmath>
 +
<cmath>CJ^2=2^2+1^2-2\cdot2\cdot1\cdot\cos{120^{\circ}}.</cmath>
 +
<cmath>CJ^2=5-2\cdot2\cdot\frac{-1}{2}=7.</cmath> <cmath>CJ=\sqrt{7}.</cmath>
 +
<cmath>\textbf{Step 3:} </cmath>
 +
Now since we have all side lengths of <math>\triangle{CAJ}</math> we can find <math>\cos{\angle{CAJ}}.</math> Applying LoC again on <math>\triangle{CAJ}</math> we have,
 +
<cmath>CJ^2=CA^2+AJ^2-2\cdot{CA}\cdot{AJ}\cdot\cos{\angle{CAJ}}. </cmath>
 +
<cmath>{\sqrt{7}}^2={\sqrt{13}}^2+{3}^2-2\cdot3\cdot{\sqrt{13}}\cdot\cos{\angle{CAJ}}.</cmath>
 +
<cmath>7=22-6{\sqrt{13}}\cdot\cos{\angle{CAJ}}.</cmath>
 +
<cmath>\frac{-15}{-6{\sqrt{13}}}=\frac{5\sqrt{13}}{26}=\cos{\angle{CAJ}}.</cmath>
 +
<cmath>\textbf{Step 4:} </cmath>
 +
We can solve for the area using the sin area formula which is <math>\frac{1}{2}\cdot{AC}\cdot{AB}\sin{\angle{CAJ}}.</math> To find <math>\sin{\angle{CAJ}}</math> we use the well known fact <math>\sin^2{x}+\cos^2{x}=1.</math> So we find,
 +
<cmath>\sin^2{\angle{CAJ}}+\cos^2{\angle{CAJ}}=1.</cmath>
 +
<cmath>\sin^2{\angle{CAJ}}+(\frac{5\sqrt{13}}{26})^2=1.</cmath>
 +
<cmath>\sin^2{\angle{CAJ}}+\frac{25}{52}=1.</cmath>
 +
<cmath>\sin^2{\angle{CAJ}}=\frac{27}{52}.</cmath>
 +
<cmath>\sin{\angle{CAJ}}=\frac{3\sqrt{39}}{26}.</cmath>
 +
Finally to wrap up we can find the area of <math>\triangle{ABC}</math> using the sin area formula,
 +
<cmath>[ABC]=\frac{1}{2}\cdot{AC}\cdot{AB}\cdot\sin{\angle{CAJ}}.</cmath>
 +
<cmath>[ABC]=\frac{1}{2}\cdot\sqrt{13}\cdot{6}\cdot\frac{3\sqrt{39}}{26}=\frac{9\sqrt{3}}{2}.</cmath>
 +
Therefore our answer is <math>\boxed{\textbf{(B) } \frac{9}{2} \sqrt3.}</math>
 +
 +
~[[User:Mathkiddus|mathkiddus]]
 +
==Solution 7(coordinate bash)==
 +
Assume we set A as <math>(0, 0)</math>. The line AB can be split into 4 equal sections, easily noticed in the picture. Not that the first equal section, starting at A. When we follow the line AB, we see that it's a right angle, noticing its a 30, 60, 90 triangle. Because the hypothenuse of that triangle is <math>\sqrt{3}</math>. Using the 30, 60, 90 ratio, we see that one of those equal sections is 3/2. Making the coordinate of B, <math>(6, 0)</math>.
 +
 +
Now, we must find the coordinate of C. Note that when we drop C down to the perpindicular of AB, there is a <math>x</math> component to C, and a <math>y</math> component to C. To find the X component, we see that it's one equal section found before as 3/2, and another section equal to 1, given in the question, making it <math>x</math> = 5/2. The Y component can be seen as another two sections. The two green sections marked in solution 1. One is <math>\sqrt{3}/2</math> due to the same 30 60 90 triangle we found in the first part of the solution. And the other part is <math>\sqrt{3}</math>, given in the question. Making <math>y</math> = <math>\frac{3}{2} \sqrt3</math>.
 +
So we see that C = (<math>5/2</math>, <math>\frac{3}{2} \sqrt3</math>)
 +
 +
Using shoelace theorem, we get to get  <math>\boxed{  \textbf{(B) } \frac{9}{2} \sqrt3}.</math>
 +
 +
sorry for no diagrams D:
 +
 +
 +
-marcus
 +
 +
== Video Solution by Power Solve ==
 +
https://www.youtube.com/watch?v=bxC_UENbmNk
 +
 +
== Video Solution by Pi Academy (Fast and Easy⚡️🚀) ==
 +
 +
https://youtu.be/hcpej1uRYu4?si=-DekbEWkAg_c6nsg
 +
 +
 +
==Video Solution by Innovative Minds ==
 +
 +
https://www.youtube.com/watch?v=bhC58BB3kJA
 +
 +
~i_am_suk_at_math_2
 +
 +
==Video Solution by SpreadTheMathLove==
 +
https://www.youtube.com/watch?v=6SQ74nt3ynw
 +
==Video Solution by Just Math⚡==
 +
https://www.youtube.com/watch?v=OjdLNjiO5Qw
 +
 +
==See also==
 +
{{AMC10 box|year=2024|ab=A|num-b=21|num-a=23}}
 +
{{MAA Notice}}

Latest revision as of 21:40, 6 December 2024

Problem

Let $\mathcal K$ be the kite formed by joining two right triangles with legs $1$ and $\sqrt3$ along a common hypotenuse. Eight copies of $\mathcal K$ are used to form the polygon shown below. What is the area of triangle $\Delta ABC$?

Asset-ddfea426a1acee64ea44467d8aa8797a.png

$\textbf{(A) }2+3\sqrt3\qquad\textbf{(B) }\dfrac92\sqrt3\qquad\textbf{(C) }\dfrac{10+8\sqrt3}{3}\qquad\textbf{(D) }8\qquad\textbf{(E) }5\sqrt3$

Solution 1

2024 AMC 10 A Diagram Problem 22.png

First, we should find the length of $AB$. In order to do this, as we see in the diagram, it can be split into 4 equal sections. Since diagram $K$ shows us that it is made up of two ${30,60,90}$ triangles, then the triangle outlined in red must be a $30,60,90$ triangle, as ${30+30=60}$, and the two lines are perpendicular (it is proveable, but during competition, it is best to assume this is true, as the diagram is draw pretty well to scale). Also, since we know the length of the longest side of the red triangle is ${\sqrt3}$, then the side we are looking for, which is outlined in blue, must be $\frac{3}{2}$ by the ${1,\sqrt3, 2}$ relationship of ${30,60,90}$ triangles. Therefore $AB$, which is the base of the triangle we are looking, for must be $6.$


Now all we have to do is find the height. We can split the height into 2 sections, the green and the light green. The green section must be ${\sqrt3}$, as $K$ shows us. Also, the light green section must be equal to ${\frac{\sqrt3}{2}}$, as in the previous paragraph, the triangle outlined in red is $30,60,90$. Then, the green section, which is the height, must be ${\sqrt3}+{\frac{\sqrt3}{2}}$, which is just ${\frac{3\sqrt3}{2}}$.


Then the area of the triangle must be ${\frac{1}{2}}\cdot {b} \cdot {h}$, which is just $\boxed{ \textbf{(B) } \frac{9}{2} \sqrt3}.$

~Solution by HappySharks ~Minor Edits by mathkiddus

Solution 2

Let $\mathcal K$ be quadrilateral $MNOP$. Drawing line $MO$ splits the triangle into $\Delta MNO$. Drawing the altitude from $N$ to point $Q$ on line $MO$, we know $NQ$ is $\frac{\sqrt{3}}{2}$, $MQ$ is $\frac{3}{2}$, and $QO$ is $\frac{1}{2}$.

Screenshot 2024-11-08 2.33.52 PM.png

Due to the many similarities present, we can find that $AB$ is $4(MQ)$, and the height of $\Delta ABC$ is $NQ+MN$

$AB$ is $4(\frac{3}{2})=6$ and the height of $\Delta ABC$ is $\sqrt3+\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}$.

Solving for the area of $\Delta ABC$ gives $6\cdot\frac{3\sqrt{3}}{2}\cdot\frac{1}{2}$ which is $\boxed{\textbf{(B) }\dfrac92\sqrt3}$

~9897 (latex beginner here)

~i_am_suk_at_math(very minor latex edits)

Solution 3

Let's start by looking at kite $\mathcal K$. We can quickly deduce based off of the side lengths that the kite can be split into two $30-60-90$ triangles. Going back to the triangle $\triangle ABC$, focus on side $AB$. There are $4$ kites, they are all either reflected over the line $AB$ or a line perpendicular to $AB$, meaning the length of $AB$ can be split up into 4 equal parts.

Pick out the bottom-left kite, and we can observe that the kite and the triangle formed by the intersection of the kite and $\Delta ABC$ share a $60$ degree angle. (this was deduced from the $30-60-90$ triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a $90^{\circ}$ angle. Because that is also a $30-60-90$ triangle with a hypotenuse of $\sqrt3$, so we find the length of AB to be $4*3/2$, which is $6$.

Then, we can drop an altitude from $C$ to $AB$. We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and $\Delta ABC$. (Look at the line formed on the left of $C$ that drops down to $AB$ if you are confused) We already have those values from the $30-60-90$ triangles, so we can just plug it into the triangle area formula, $bh/2$. We get \[6\cdot\dfrac{\sqrt3+\frac{\sqrt3}{2}}{2}\rightarrow3\cdot(\sqrt3+\dfrac{\sqrt3}{2})\rightarrow3\cdot\dfrac{\sqrt3}{2}\rightarrow\boxed{\textbf{(B) }\dfrac92\sqrt3}\]

~YTH

~WIP (Header)

~Tacos_are_yummy_1 ($\LaTeX$ & Formatting)

Solution 4

202410A 23v2.png

~mathboy282

Solution 5

Let the point of intersection of $AB$ and the kite with $A$ as vertex be $D$.

Let the left kite with $C$ as a vertex touch the kite with $A$ as vertex at point $E$.

$\triangle ADE$ is a $30-60-90$ so $AD = \frac{3}{2}$ and $DE = \frac{\sqrt3}{2}$.

So, $AB = 4\cdot AD = 6$ and $CD=CE+DE= \frac{3\sqrt3}{2}$, and the area is $\frac12\cdot AB \cdot CD = \boxed{ \textbf{(B) } \frac{9}{2} \sqrt3}.$

~Mintylemon66

Solution 6(trig bash)

Screenshot 2024-11-09 201440.png \[\textbf{Step 1:}\] As stated in the solutions above we can easily find that $AB$ is split into $4$ equal parts, so we have $AB=4(AE)$ We can calculate $AE,$ by using $AA$ similarity to find $\triangle{ADE}$ is a $30-60-90$ triangle, therefore we have $AD=\sqrt{3},DE=\frac{\sqrt{3}}{2},$ and finally $AE=\frac{3}{2},$ therefore $AB=4(AE)=4(\frac{3}{2})=6.$ Similarly we have $CF$ is congruent to $FG,$ therefore $CF=FG=1.$ Next we have $AD$ is congruent to $DF$ telling us $AF=AD+DF=2(AD)=2\sqrt{3}.$ Noticing $\triangle{CFA}$ is right, we apply Pythagorean theorem to $\triangle{CFA}$ to find \[AC^2=CF^2+AF^2\] \[AC^2=(1)^2+(2\sqrt{3})^2=13\] \[AC=\sqrt{13}.\] \[\textbf{Step 2:}\] Next we would like to calculate CJ, As said before $CF=FG=1$ so $CG=2.$ We know the inscribed angle between CG and GJ is $60\cdot2=120,$ and finally we know $GJ=1.$ So we apply LoC on triangle CGJ in order to find CJ. \[CJ^2=CG^2+GJ^2-2\cdot{CG}\cdot{GJ}\cdot\cos{120^{\circ}}.\] \[CJ^2=2^2+1^2-2\cdot2\cdot1\cdot\cos{120^{\circ}}.\] \[CJ^2=5-2\cdot2\cdot\frac{-1}{2}=7.\] \[CJ=\sqrt{7}.\] \[\textbf{Step 3:}\] Now since we have all side lengths of $\triangle{CAJ}$ we can find $\cos{\angle{CAJ}}.$ Applying LoC again on $\triangle{CAJ}$ we have, \[CJ^2=CA^2+AJ^2-2\cdot{CA}\cdot{AJ}\cdot\cos{\angle{CAJ}}.\] \[{\sqrt{7}}^2={\sqrt{13}}^2+{3}^2-2\cdot3\cdot{\sqrt{13}}\cdot\cos{\angle{CAJ}}.\] \[7=22-6{\sqrt{13}}\cdot\cos{\angle{CAJ}}.\] \[\frac{-15}{-6{\sqrt{13}}}=\frac{5\sqrt{13}}{26}=\cos{\angle{CAJ}}.\] \[\textbf{Step 4:}\] We can solve for the area using the sin area formula which is $\frac{1}{2}\cdot{AC}\cdot{AB}\sin{\angle{CAJ}}.$ To find $\sin{\angle{CAJ}}$ we use the well known fact $\sin^2{x}+\cos^2{x}=1.$ So we find, \[\sin^2{\angle{CAJ}}+\cos^2{\angle{CAJ}}=1.\] \[\sin^2{\angle{CAJ}}+(\frac{5\sqrt{13}}{26})^2=1.\] \[\sin^2{\angle{CAJ}}+\frac{25}{52}=1.\] \[\sin^2{\angle{CAJ}}=\frac{27}{52}.\] \[\sin{\angle{CAJ}}=\frac{3\sqrt{39}}{26}.\] Finally to wrap up we can find the area of $\triangle{ABC}$ using the sin area formula, \[[ABC]=\frac{1}{2}\cdot{AC}\cdot{AB}\cdot\sin{\angle{CAJ}}.\] \[[ABC]=\frac{1}{2}\cdot\sqrt{13}\cdot{6}\cdot\frac{3\sqrt{39}}{26}=\frac{9\sqrt{3}}{2}.\] Therefore our answer is $\boxed{\textbf{(B) } \frac{9}{2} \sqrt3.}$

~mathkiddus

Solution 7(coordinate bash)

Assume we set A as $(0, 0)$. The line AB can be split into 4 equal sections, easily noticed in the picture. Not that the first equal section, starting at A. When we follow the line AB, we see that it's a right angle, noticing its a 30, 60, 90 triangle. Because the hypothenuse of that triangle is $\sqrt{3}$. Using the 30, 60, 90 ratio, we see that one of those equal sections is 3/2. Making the coordinate of B, $(6, 0)$.

Now, we must find the coordinate of C. Note that when we drop C down to the perpindicular of AB, there is a $x$ component to C, and a $y$ component to C. To find the X component, we see that it's one equal section found before as 3/2, and another section equal to 1, given in the question, making it $x$ = 5/2. The Y component can be seen as another two sections. The two green sections marked in solution 1. One is $\sqrt{3}/2$ due to the same 30 60 90 triangle we found in the first part of the solution. And the other part is $\sqrt{3}$, given in the question. Making $y$ = $\frac{3}{2} \sqrt3$. So we see that C = ($5/2$, $\frac{3}{2} \sqrt3$)

Using shoelace theorem, we get to get $\boxed{ \textbf{(B) } \frac{9}{2} \sqrt3}.$

sorry for no diagrams D:


-marcus

Video Solution by Power Solve

https://www.youtube.com/watch?v=bxC_UENbmNk

Video Solution by Pi Academy (Fast and Easy⚡️🚀)

https://youtu.be/hcpej1uRYu4?si=-DekbEWkAg_c6nsg


Video Solution by Innovative Minds

https://www.youtube.com/watch?v=bhC58BB3kJA

~i_am_suk_at_math_2

Video Solution by SpreadTheMathLove

https://www.youtube.com/watch?v=6SQ74nt3ynw

Video Solution by Just Math⚡

https://www.youtube.com/watch?v=OjdLNjiO5Qw

See also

2024 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_10A_Problems/Problem_22&oldid=236304"