Difference between revisions of "2001 USAMO Problems/Problem 2"
5849206328x (talk | contribs) (→Solution: official solution) |
5849206328x (talk | contribs) (→Solution 2: added images) |
||
| Line 25: | Line 25: | ||
'''Lemma''': Segment <math>D_1Q</math> is a diameter of circle <math>\omega</math>. | '''Lemma''': Segment <math>D_1Q</math> is a diameter of circle <math>\omega</math>. | ||
| − | + | <center>[[File:2001usamo2-1.png]]</center> | |
''Proof'': Let <math>I</math> be the center of circle <math>\omega</math>, i.e., <math>I</math> is the incenter of triangle <math>ABC</math>. Extend segment <math>D_1I</math> through <math>I</math> to intersect circle <math>\omega</math> again at <math>Q'</math>, and extend segment <math>AQ'</math> through <math>Q'</math> to intersect segment <math>BC</math> at <math>D'</math>. We show that <math>D_2 = D'</math>, which in turn implies that <math>Q = Q'</math>, that is, <math>D_1Q</math> is a diameter of <math>\omega</math>. | ''Proof'': Let <math>I</math> be the center of circle <math>\omega</math>, i.e., <math>I</math> is the incenter of triangle <math>ABC</math>. Extend segment <math>D_1I</math> through <math>I</math> to intersect circle <math>\omega</math> again at <math>Q'</math>, and extend segment <math>AQ'</math> through <math>Q'</math> to intersect segment <math>BC</math> at <math>D'</math>. We show that <math>D_2 = D'</math>, which in turn implies that <math>Q = Q'</math>, that is, <math>D_1Q</math> is a diameter of <math>\omega</math>. | ||
| Line 40: | Line 40: | ||
that is, <math>D' = D_2</math>, as desired. <math>\blacksquare</math> | that is, <math>D' = D_2</math>, as desired. <math>\blacksquare</math> | ||
| − | |||
Now we prove our main result. Let <math>M_1</math> and <math>M_2</math> be the respective midpoints of segments <math>BC</math> and <math>CA</math>. Then <math>M_1</math> is also the midpoint of segment <math>D_1D_2</math>, from which it follows that <math>IM_1</math> is the midline of triangle <math>D_1QD_2</math>. Hence | Now we prove our main result. Let <math>M_1</math> and <math>M_2</math> be the respective midpoints of segments <math>BC</math> and <math>CA</math>. Then <math>M_1</math> is also the midpoint of segment <math>D_1D_2</math>, from which it follows that <math>IM_1</math> is the midline of triangle <math>D_1QD_2</math>. Hence | ||
<cmath>QD_2 = 2IM_1</cmath> | <cmath>QD_2 = 2IM_1</cmath> | ||
and <math>AD_2\parallel M_1I</math>. Similarly, we can prove that <math>BE_2\parallel M_2I</math>. | and <math>AD_2\parallel M_1I</math>. Similarly, we can prove that <math>BE_2\parallel M_2I</math>. | ||
| − | + | <center>[[File:2001usamo2-2.png]]</center> | |
| + | |||
Let <math>G</math> be the centroid of triangle <math>ABC</math>. Thus segments <math>AM_1</math> and <math>BM_2</math> intersect at <math>G</math>. Define transformation <math>\mathbf{H}_2</math> as the dilation with its center at <math>G</math> and ratio <math>-1/2</math>. Then <math>\mathbf{H}_2(A) = M_1</math> and <math>\mathbf{H}_2(B) = M_2</math>. Under the dilation, parallel lines go to parallel lines and the intersection of two lines goes to the intersection of their images. Since <math>AD_2\parallel M_1I</math> and <math>BE_2\parallel M_2I</math>, <math>\mathbf{H}_2</math> maps lines <math>AD_2</math> and <math>BE_2</math> to lines <math>M_1I</math> and <math>M_2I</math>, respectively. It also follows that <math>\mathbf{H}_2(I) = P</math> and | Let <math>G</math> be the centroid of triangle <math>ABC</math>. Thus segments <math>AM_1</math> and <math>BM_2</math> intersect at <math>G</math>. Define transformation <math>\mathbf{H}_2</math> as the dilation with its center at <math>G</math> and ratio <math>-1/2</math>. Then <math>\mathbf{H}_2(A) = M_1</math> and <math>\mathbf{H}_2(B) = M_2</math>. Under the dilation, parallel lines go to parallel lines and the intersection of two lines goes to the intersection of their images. Since <math>AD_2\parallel M_1I</math> and <math>BE_2\parallel M_2I</math>, <math>\mathbf{H}_2</math> maps lines <math>AD_2</math> and <math>BE_2</math> to lines <math>M_1I</math> and <math>M_2I</math>, respectively. It also follows that <math>\mathbf{H}_2(I) = P</math> and | ||
<cmath>\frac{IM_1}{AP} = \frac{GM_1}{AG} = \frac{1}{2}</cmath> | <cmath>\frac{IM_1}{AP} = \frac{GM_1}{AG} = \frac{1}{2}</cmath> | ||
Revision as of 20:59, 6 July 2014
Contents
[hide]Problem
Let ![]() be a triangle and let
be a triangle and let ![]() be its incircle. Denote by
be its incircle. Denote by ![]() and
and ![]() the points where
the points where ![]() is tangent to sides
is tangent to sides ![]() and
and ![]() , respectively. Denote by
, respectively. Denote by ![]() and
and ![]() the points on sides
the points on sides ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() and
and ![]() , and denote by
, and denote by ![]() the point of intersection of segments
the point of intersection of segments ![]() and
and ![]() . Circle
. Circle ![]() intersects segment
intersects segment ![]() at two points, the closer of which to the vertex
at two points, the closer of which to the vertex ![]() is denoted by
is denoted by ![]() . Prove that
. Prove that ![]() .
.
Solution
Solution 1
It is well known that the excircle opposite ![]() is tangent to
is tangent to ![]() at the point
at the point ![]() . (Proof: let the points of tangency of the excircle with the lines
. (Proof: let the points of tangency of the excircle with the lines ![]() be
be ![]() respectively. Then
respectively. Then ![]() . It follows that
. It follows that ![]() , and
, and ![]() , so
, so ![]() .)
.)
Now consider the homothety that carries the incircle of ![]() to its excircle. The homothety also carries
to its excircle. The homothety also carries ![]() to
to ![]() (since
(since ![]() are collinear), and carries the tangency points
are collinear), and carries the tangency points ![]() to
to ![]() . It follows that
. It follows that ![]() .
.
![[asy] pathpen = linewidth(0.7); size(300); pen d = linetype("4 4") + linewidth(0.6); pair B=(0,0), C=(10,0), A=7*expi(1),O=D(incenter(A,B,C)),D1 = D(MP("D_1",foot(O,B,C))),E1 = D(MP("E_1",foot(O,A,C),NE)),E2 = D(MP("E_2",C+A-E1,NE)); /* arbitrary points */ /* ugly construction for OA */ pair Ca = 2C-A, Cb = bisectorpoint(Ca,C,B), OA = IP(A--A+10*(O-A),C--C+50*(Cb-C)), D2 = D(MP("D_2",foot(OA,B,C))), Fa=2B-A, Ga=2C-A, F=MP("F",D(foot(OA,B,Fa)),NW), G=MP("G",D(foot(OA,C,Ga)),NE); D(OA); D(MP("A",A,N)--MP("B",B,NW)--MP("C",C,NE)--cycle); D(incircle(A,B,C)); D(CP(OA,D2),d); D(B--Fa,linewidth(0.6)); D(C--Ga,linewidth(0.6)); D(MP("P",IP(D(A--D2),D(B--E2)),NNE)); D(MP("Q",IP(incircle(A,B,C),A--D2),SW)); clip((-20,-10)--(-20,20)--(20,20)--(20,-10)--cycle); [/asy]](http://latex.artofproblemsolving.com/d/b/6/db6875d6724835163f466dad6bbadb2278bef967.png)
By Menelaus' Theorem on ![]() with segment
with segment ![]() , it follows that
, it follows that ![]() . It easily follows that
. It easily follows that ![]() .
. ![]()
Solution 2
The key observation is the following lemma.
Lemma: Segment ![]() is a diameter of circle
is a diameter of circle ![]() .
.
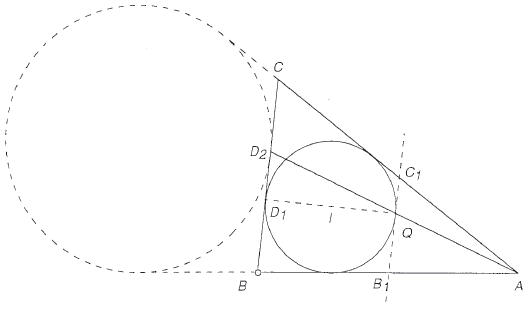
Proof: Let ![]() be the center of circle
be the center of circle ![]() , i.e.,
, i.e., ![]() is the incenter of triangle
is the incenter of triangle ![]() . Extend segment
. Extend segment ![]() through
through ![]() to intersect circle
to intersect circle ![]() again at
again at ![]() , and extend segment
, and extend segment ![]() through
through ![]() to intersect segment
to intersect segment ![]() at
at ![]() . We show that
. We show that ![]() , which in turn implies that
, which in turn implies that ![]() , that is,
, that is, ![]() is a diameter of
is a diameter of ![]() .
.
Let ![]() be the line tangent to circle
be the line tangent to circle ![]() at
at ![]() , and let
, and let ![]() intersect the segments
intersect the segments ![]() and
and ![]() at
at ![]() and
and ![]() , respectively. Then
, respectively. Then ![]() is an excircle of triangle
is an excircle of triangle ![]() . Let
. Let ![]() denote the dilation with its center at
denote the dilation with its center at ![]() and ratio
and ratio ![]() . Since
. Since ![]() and
and ![]() ,
, ![]() . Hence
. Hence ![]() . Thus
. Thus ![]() ,
, ![]() , and
, and ![]() . It also follows that an excircle
. It also follows that an excircle ![]() of triangle
of triangle ![]() is tangent to the side
is tangent to the side ![]() at
at ![]() .
.
It is well known that
![]() We compute
We compute ![]() . Let
. Let ![]() and
and ![]() denote the points of tangency of circle
denote the points of tangency of circle ![]() with rays
with rays ![]() and
and ![]() , respectively. Then by equal tangents,
, respectively. Then by equal tangents, ![]() ,
, ![]() , and
, and ![]() . Hence
. Hence
![]() It follows that
It follows that
![]() Combining these two equations yields
Combining these two equations yields ![]() . Thus
. Thus
![]() that is,
that is, ![]() , as desired.
, as desired. ![]()
Now we prove our main result. Let ![]() and
and ![]() be the respective midpoints of segments
be the respective midpoints of segments ![]() and
and ![]() . Then
. Then ![]() is also the midpoint of segment
is also the midpoint of segment ![]() , from which it follows that
, from which it follows that ![]() is the midline of triangle
is the midline of triangle ![]() . Hence
. Hence
![]() and
and ![]() . Similarly, we can prove that
. Similarly, we can prove that ![]() .
.
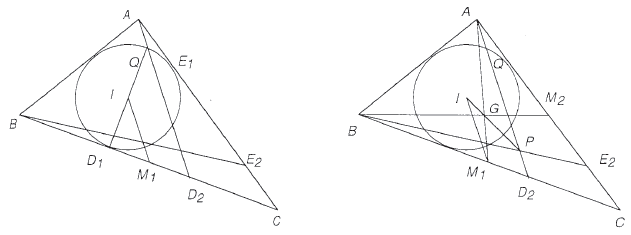
Let ![]() be the centroid of triangle
be the centroid of triangle ![]() . Thus segments
. Thus segments ![]() and
and ![]() intersect at
intersect at ![]() . Define transformation
. Define transformation ![]() as the dilation with its center at
as the dilation with its center at ![]() and ratio
and ratio ![]() . Then
. Then ![]() and
and ![]() . Under the dilation, parallel lines go to parallel lines and the intersection of two lines goes to the intersection of their images. Since
. Under the dilation, parallel lines go to parallel lines and the intersection of two lines goes to the intersection of their images. Since ![]() and
and ![]() ,
, ![]() maps lines
maps lines ![]() and
and ![]() to lines
to lines ![]() and
and ![]() , respectively. It also follows that
, respectively. It also follows that ![]() and
and
![]() or
or
![]() This yields
This yields
![]() as desired.
as desired.
Note: We used directed lengths in our calculations to avoid possible complications caused by the different shapes of triangle ![]() .
.
See also
| 2001 USAMO (Problems • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









