Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2001 USAMO Problems/Problem 6"

(→‎Solution: official solution)
m (fixed the qedsymbol)
 
Line 10: Line 10:
 
''Proof'': Assume without loss of generality that <math>BC\parallel AD</math>, and that rays <math>AB</math> and <math>DC</math> meet at <math>P</math>. Let <math>I</math> be the incenter of triangle <math>PAC</math>, and let line <math>l</math> bisect <math>\angle APD</math>. Then <math>I</math> is on <math>l</math>, so reflecting everything across line <math>l</math> shows that <math>I</math> is also the incenter of triangle <math>PDB</math>. Therefore,
 
''Proof'': Assume without loss of generality that <math>BC\parallel AD</math>, and that rays <math>AB</math> and <math>DC</math> meet at <math>P</math>. Let <math>I</math> be the incenter of triangle <math>PAC</math>, and let line <math>l</math> bisect <math>\angle APD</math>. Then <math>I</math> is on <math>l</math>, so reflecting everything across line <math>l</math> shows that <math>I</math> is also the incenter of triangle <math>PDB</math>. Therefore,
 
<cmath>\frac{p + a + c}{3} = i = \frac{p + b + d}{3}.</cmath>
 
<cmath>\frac{p + a + c}{3} = i = \frac{p + b + d}{3}.</cmath>
−
Hence <math>a + c = b + d</math>, as desired.<math>\qedsymbol</math>
+
Hence <math>a + c = b + d</math>, as desired.<math>\blacksquare</math>
  
 
<center>[[File:2001usamo6-1.png]]</center>
 
<center>[[File:2001usamo6-1.png]]</center>

Latest revision as of 17:11, 22 February 2016

Problem

Each point in the plane is assigned a real number such that, for any triangle, the number at the center of its inscribed circle is equal to the arithmetic mean of the three numbers at its vertices. Prove that all points in the plane are assigned the same number.

Solution

We label each upper case point with the corresponding lower case letter as its assigned number. The key step is the following lemma.

Lemma: If $ABCD$ is an isosceles trapezoid, then $a + c = b + d$.

Proof: Assume without loss of generality that $BC\parallel AD$, and that rays $AB$ and $DC$ meet at $P$. Let $I$ be the incenter of triangle $PAC$, and let line $l$ bisect $\angle APD$. Then $I$ is on $l$, so reflecting everything across line $l$ shows that $I$ is also the incenter of triangle $PDB$. Therefore, \[\frac{p + a + c}{3} = i = \frac{p + b + d}{3}.\] Hence $a + c = b + d$, as desired.$\blacksquare$

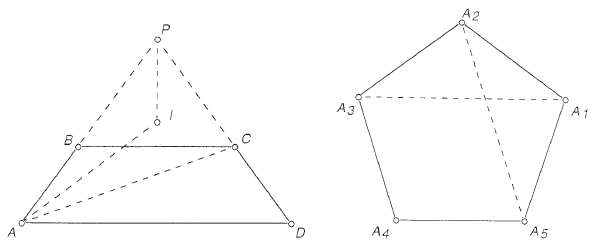
2001usamo6-1.png

For any two distinct points $A_1$ and $A_2$ in the plane, we construct a regular pentagon $A_1A_2A_3A_4A_5$. Applying the lemma to isosceles trapezoids $A_1A_3A_4A_5$ and $A_2A_3A_4A_5$ yields \[a_1 + a_4 = a_3 + a_5\quad\text{and}\quad a_2 + a_4 = a_3 + a_5.\] Hence $a_1 = a_2$. Since $A_1$ and $A_2$ were arbitrary, all points in the plane are assigned the same number.

See also

2001 USAMO (Problems • Resources)
Preceded by
Problem 5 		Followed by
Last question
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2001_USAMO_Problems/Problem_6&oldid=76980"