Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME I Problems/Problem 8"

(→‎Solution 1)
m (→‎Solution 3 (Simple Geometry))
 
(56 intermediate revisions by 10 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
Equilateral triangle <math>\triangle ABC</math> is inscribed in circle <math>\omega</math> with radius <math>18.</math> Circle <math>\omega_A</math> is tangent to sides <math>\overline{AB}</math> and <math>\overline{AC}</math> and is internally tangent to <math>\omega</math>. Circles <math>\omega_B</math> and <math>\omega_C</math> are defined analogously. Circles <math>\omega_A</math>, <math>\omega_B</math>, and <math>\omega_C</math> meet in six points<math>-</math>two points for each pair of circles. The three intersection points closest to the vertices of <math>\triangle ABC</math> are the vertices of a large equilateral triangle in the interior of <math>\triangle ABC</math>, and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of <math>\triangle ABC</math>. The side length of the smaller equilateral triangle can be written as <math>\sqrt{a}-\sqrt{b}</math>, where <math>a</math> and <math>b</math> are positive integers. Find <math>a+b</math>.
+
Equilateral triangle <math>\triangle ABC</math> is inscribed in circle <math>\omega</math> with radius <math>18.</math> Circle <math>\omega_A</math> is tangent to sides <math>\overline{AB}</math> and <math>\overline{AC}</math> and is internally tangent to <math>\omega.</math> Circles <math>\omega_B</math> and <math>\omega_C</math> are defined analogously. Circles <math>\omega_A,</math> <math>\omega_B,</math> and <math>\omega_C</math> meet in six points---two points for each pair of circles. The three intersection points closest to the vertices of <math>\triangle ABC</math> are the vertices of a large equilateral triangle in the interior of <math>\triangle ABC,</math> and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of <math>\triangle ABC.</math> The side length of the smaller equilateral triangle can be written as <math>\sqrt{a} - \sqrt{b},</math> where <math>a</math> and <math>b</math> are positive integers. Find <math>a+b.</math>
  
 
== Diagram ==
 
== Diagram ==
 
<asy>
 
<asy>
−
unitsize(0.3cm);
+
/* Made by MRENTHUSIASM */
−
draw(circle((0,0),18));
+
size(250);
−
pair A = (9 * sqrt(3), -9);
+
pair A, B, C, W, WA, WB, WC, X, Y, Z;
−
pair B = (-9 * sqrt(3), -9);
+
A = 18*dir(90);
−
pair C = (0,18);
+
B = 18*dir(210);
−
draw(A--B--C--cycle);
+
C = 18*dir(330);
−
draw(circle((0,-6),12), gray);
+
W = (0,0);
−
draw(circle((3*sqrt(3),3),12), gray);
+
WA = 6*dir(270);
−
draw(circle((-3*sqrt(3),3),12), gray);
+
WB = 6*dir(30);
 +
WC = 6*dir(150);
 +
X = (sqrt(117)-3)*dir(270);
 +
Y = (sqrt(117)-3)*dir(30);
 +
Z = (sqrt(117)-3)*dir(150);
 +
filldraw(X--Y--Z--cycle,green,dashed);
 +
draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue);
 +
draw(Circle(W,18)^^A--B--C--cycle);
 +
dot("$A$",A,1.5*dir(A),linewidth(4));
 +
dot("$B$",B,1.5*dir(B),linewidth(4));
 +
dot("$C$",C,1.5*dir(C),linewidth(4));
 +
dot("$\omega$",W,1.5*dir(270),linewidth(4));
 +
dot("$\omega_A$",WA,1.5*dir(-WA),linewidth(4));
 +
dot("$\omega_B$",WB,1.5*dir(-WB),linewidth(4));
 +
dot("$\omega_C$",WC,1.5*dir(-WC),linewidth(4));
 +
</asy>
 +
~MRENTHUSIASM ~ihatemath123
  
−
pair X = (0, 3-sqrt(117));
+
==Solution 1 (Coordinate Geometry)==
−
pair Y = ( (sqrt(351)-sqrt(27))/2, (sqrt(117)-3)/2 );
 
−
pair Z = ( (sqrt(27) - sqrt(351))/2, (sqrt(117)-3)/2 );
 
−
dot(X);
 
−
dot(Y);
 
−
dot(Z);
 
  
−
draw(X--Y--Z--cycle, dashed);
+
We can extend <math>AB</math> and <math>AC</math> to <math>B'</math> and <math>C'</math> respectively such that circle <math>\omega_A</math> is the incircle of <math>\triangle AB'C'</math>.
 +
<asy>
 +
/* Made by MRENTHUSIASM */
 +
size(300);
 +
pair A, B, C, B1, C1, W, WA, WB, WC, X, Y, Z;
 +
A = 18*dir(90);
 +
B = 18*dir(210);
 +
C = 18*dir(330);
 +
B1 = A+24*sqrt(3)*dir(B-A);
 +
C1 = A+24*sqrt(3)*dir(C-A);
 +
W = (0,0);
 +
WA = 6*dir(270);
 +
WB = 6*dir(30);
 +
WC = 6*dir(150);
 +
X = (sqrt(117)-3)*dir(270);
 +
Y = (sqrt(117)-3)*dir(30);
 +
Z = (sqrt(117)-3)*dir(150);
 +
filldraw(X--Y--Z--cycle,green,dashed);
 +
draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue);
 +
draw(Circle(W,18)^^A--B--C--cycle);
 +
draw(B--B1--C1--C,dashed);
 +
dot("$A$",A,1.5*dir(A),linewidth(4));
 +
dot("$B$",B,1.5*(-1,0),linewidth(4));
 +
dot("$C$",C,1.5*(1,0),linewidth(4));
 +
dot("$B'$",B1,1.5*dir(B1),linewidth(4));
 +
dot("$C'$",C1,1.5*dir(C1),linewidth(4));
 +
dot("$O$",W,1.5*dir(90),linewidth(4));
 +
dot("$X$",X,1.5*dir(X),linewidth(4));
 +
dot("$Y$",Y,1.5*dir(Y),linewidth(4));
 +
dot("$Z$",Z,1.5*dir(Z),linewidth(4));
 
</asy>
 
</asy>
 +
Since the diameter of the circle is the height of this triangle, the height of this triangle is <math>36</math>. We can use inradius or equilateral triangle properties to get the inradius of this triangle is <math>12</math> (The incenter is also a centroid in an equilateral triangle, and the distance from a side to the centroid is a third of the height). Therefore, the radius of each of the smaller circles is <math>12</math>.
  
−
==Solution 1==
+
Let <math>O=\omega</math> be the center of the largest circle. We will set up a coordinate system with <math>O</math> as the origin. The center of <math>\omega_A</math> will be at <math>(0,-6)</math> because it is directly beneath <math>O</math> and is the length of the larger radius minus the smaller radius, or <math>18-12 = 6</math>. By rotating this point <math>120^{\circ}</math> around <math>O</math>, we get the center of <math>\omega_B</math>. This means that the magnitude of vector <math>\overrightarrow{O\omega_B}</math> is <math>6</math> and is at a <math>30</math> degree angle from the horizontal. Therefore, the coordinates of this point are <math>(3\sqrt{3},3)</math> and by symmetry the coordinates of the center of <math>\omega_C</math> is <math>(-3\sqrt{3},3)</math>.
  
−
We can extend <math>AB</math> and <math>AC</math> to <math>B'</math> and <math>C'</math> respectively such that circle <math>\omega_A</math> is the incircle of <math>\triangle AB'C'</math>.
+
The upper left and right circles intersect at two points, the lower of which is <math>X</math>. The equations of these two circles are:
 +
<cmath>\begin{align*}
 +
(x+3\sqrt3)^2 + (y-3)^2 &= 12^2, \\
 +
(x-3\sqrt3)^2 + (y-3)^2 &= 12^2.
 +
\end{align*}</cmath>
 +
We solve this system by subtracting to get <math>x = 0</math>. Plugging back in to the first equation, we have <math>(3\sqrt{3})^2 + (y-3)^2 = 144 \implies (y-3)^2 = 117 \implies y-3 = \pm \sqrt{117} \implies y = 3 \pm \sqrt{117}</math>. Since we know <math>X</math> is the lower solution, we take the negative value to get <math>X = (0,3-\sqrt{117})</math>.
  
 +
We can solve the problem two ways from here. We can find <math>Y</math> by rotation and use the distance formula to find the length, or we can be somewhat more clever. We notice that it is easier to find <math>OX</math> as they lie on the same vertical, <math>\angle XOY</math> is <math>120</math> degrees so we can make use of <math>30-60-90</math> triangles, and <math>OX = OY</math> because <math>O</math> is the center of triangle <math>XYZ</math>. We can draw the diagram as such:
 
<asy>
 
<asy>
−
unitsize(0.3cm);
+
/* Made by MRENTHUSIASM */
−
draw(circle((0,0),18));
+
size(300);
−
pair C = (9 * sqrt(3), -9);
+
pair A, B, C, B1, C1, W, WA, WB, WC, X, Y, Z;
−
pair B = (-9 * sqrt(3), -9);
+
A = 18*dir(90);
−
pair B2 = (-12 * sqrt(3), -18);
+
B = 18*dir(210);
−
pair C2 = (12 * sqrt(3), -18);
+
C = 18*dir(330);
 +
B1 = A+24*sqrt(3)*dir(B-A);
 +
C1 = A+24*sqrt(3)*dir(C-A);
 +
W = (0,0);
 +
WA = 6*dir(270);
 +
WB = 6*dir(30);
 +
WC = 6*dir(150);
 +
X = (sqrt(117)-3)*dir(270);
 +
Y = (sqrt(117)-3)*dir(30);
 +
Z = (sqrt(117)-3)*dir(150);
 +
filldraw(X--Y--Z--cycle,green,dashed);
 +
draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue);
 +
draw(Circle(W,18)^^A--B--C--cycle);
 +
draw(B--B1--C1--C^^W--X^^W--Y^^W--midpoint(X--Y),dashed);
 +
dot("$A$",A,1.5*dir(A),linewidth(4));
 +
dot("$B$",B,1.5*(-1,0),linewidth(4));
 +
dot("$C$",C,1.5*(1,0),linewidth(4));
 +
dot("$B'$",B1,1.5*dir(B1),linewidth(4));
 +
dot("$C'$",C1,1.5*dir(C1),linewidth(4));
 +
dot("$O$",W,1.5*dir(90),linewidth(4));
 +
dot("$X$",X,1.5*dir(X),linewidth(4));
 +
dot("$Y$",Y,1.5*dir(Y),linewidth(4));
 +
dot("$Z$",Z,1.5*dir(Z),linewidth(4));
 +
</asy>
 +
Note that <math>OX = OY = \sqrt{117} - 3</math>. It follows that
 +
<cmath>\begin{align*}
 +
XY &= 2 \cdot \frac{OX\cdot\sqrt{3}}{2} \\
 +
&= OX \cdot \sqrt{3} \\
 +
&= (\sqrt{117}-3) \cdot \sqrt{3} \\
 +
&= \sqrt{351}-\sqrt{27}.
 +
\end{align*}</cmath>
 +
Finally, the answer is <math>351+27 = \boxed{378}</math>.
 +
 
 +
~KingRavi
  
−
pair A = (0,18);
+
==Solution 2 (Euclidean Geometry)==
−
draw(A--B--C--cycle);
 
−
draw(circle((0,-6),12), gray);
 
−
draw(circle((3*sqrt(3),3),12), gray);
 
−
draw(circle((-3*sqrt(3),3),12), gray);
 
  
−
draw(B--B2,dashed);
+
<asy>
−
draw(C--C2,dashed);
+
/* Made by MRENTHUSIASM */
−
draw(B2--C2,dashed);
+
/* Modified by isabelchen */
 +
size(250);
 +
pair A, B, C, W, WA, WB, WC, X, Y, Z, D, E;
 +
A = 18*dir(90);
 +
B = 18*dir(210);
 +
C = 18*dir(330);
 +
W = (0,0);
 +
WA = 6*dir(270);
 +
WB = 6*dir(30);
 +
WC = 6*dir(150);
 +
X = (sqrt(117)-3)*dir(270);
 +
Y = (sqrt(117)-3)*dir(30);
 +
Z = (sqrt(117)-3)*dir(150);
 +
D = intersectionpoint(Circle(WA,12),A--C);
 +
E = intersectionpoints(Circle(WB,12),Circle(WC,12))[0];
 +
filldraw(X--Y--Z--cycle,green,dashed);
 +
draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue);
 +
draw(Circle(W,18)^^A--B--C--cycle);
 +
dot("$A$",A,1.5*dir(A),linewidth(4));
 +
dot("$B$",B,1.5*dir(B),linewidth(4));
 +
dot("$C$",C,1.5*dir(C),linewidth(4));
 +
dot("$\omega$",W,1.5*dir(270),linewidth(4));
 +
dot("$\omega_A$",WA,1.5*dir(-WA),linewidth(4));
 +
dot("$\omega_B$",WB,1.5*dir(-WB),linewidth(4));
 +
dot("$\omega_C$",WC,1.5*dir(-WC),linewidth(4));
 +
dot("$X$",X,1.5*dir(X),linewidth(4));
 +
dot("$Y$",Y,1.5*dir(Y),linewidth(4));
 +
dot("$Z$",Z,1.5*dir(Z),linewidth(4));
 +
dot("$E$",E,1.5*dir(E),linewidth(4));
 +
dot("$D$",D,1.5*dir(D),linewidth(4));
 +
draw(WC--WB^^WC--X^^WC--E^^WA--D^^A--X);
 +
</asy>
 +
For equilateral triangle with side length <math>l</math>, height <math>h</math>, and circumradius <math>r</math>, there are relationships: <math>h = \frac{\sqrt{3}}{2} l</math>, <math>r = \frac{2}{3} h = \frac{\sqrt{3}}{3} l</math>, and <math>l = \sqrt{3}r</math>.
  
−
dot(B2);
+
There is a lot of symmetry in the figure. The radius of the big circle <math>\odot \omega</math> is <math>R = 18</math>, let the radius of the small circles <math>\odot \omega_A</math>, <math>\odot \omega_B</math>, <math>\odot \omega_C</math> be <math>r</math>.
−
dot(C2);
 
  
−
pair X = (0, 3-sqrt(117));
+
We are going to solve this problem in <math>3</math> steps:
−
pair Y = ( (sqrt(351)-sqrt(27))/2, (sqrt(117)-3)/2 );
 
−
pair Z = ( (sqrt(27) - sqrt(351))/2, (sqrt(117)-3)/2 );
 
−
dot(X);
 
−
dot(Y);
 
−
dot(Z);
 
−
dot((0,0));
 
−
label("$O$",(0,0),N);
 
  
−
label("$A$",A,N);
+
<math>\textbf{Step 1:}</math>
−
label("$B$",B,W);
 
−
label("$C$",C,E);
 
−
label("$B'$",B2,W);
 
−
label("$C'$",C2,E);
 
−
label("$X$",X,S);
 
−
label("$Y$",Y,E);
 
−
label("$Z$",Z,W);
 
  
 +
We have <math>\triangle A \omega_A D</math> is a <math>30-60-90</math> triangle, and <math>A \omega_A = 2 \cdot \omega_A D</math>, <math>A \omega_A = 2R-r</math> (<math>\odot \omega</math> and <math>\odot \omega_A</math> are tangent), and <math>\omega_A D = r</math>. So, we get <math>2R-r = 2r</math> and <math>r = \frac{2}{3} \cdot R = 12</math>.
  
−
draw(X--Y--Z--cycle, dashed);
+
Since <math>\odot \omega</math> and <math>\odot \omega_A</math> are tangent, we get <math>\omega \omega_A = R - r = \frac{1}{3} \cdot R = 6</math>.
−
</asy>
 
  
 +
Note that <math>\triangle \omega_A \omega_B \omega_C</math> is an equilateral triangle, and <math>\omega</math> is its center, so <math>\omega_B \omega_C = \sqrt{3} \cdot \omega \omega_A = 6 \sqrt{3}</math>.
  
−
Since the diameter of the circle is the height of this triangle, the height of this triangle is <math>36</math>. We can use inradius or equilateral triangle properties to get the inradius of this triangle is <math>12</math> (The incenter is also a centroid in an equilateral triangle, and the distance from a side to the centroid is a third of the height). Therefore, the radius of each of the smaller circles is <math>12</math>.
+
<math>\textbf{Step 2:}</math>  
  
−
Let <math>O</math> be the center of the largest circle. We will set up a coordinate system with <math>O</math> as the origin. The center of <math>\omega_A</math> will be at <math>(0,-6)</math> because it is directly beneath <math>O</math> and is the length of the larger radius minus the smaller radius, or <math>18-12 = 6</math>. By rotating this point <math>120^{\circ}</math> around <math>O</math>, we get the center of <math>\omega_B</math>. This means that the magnitude of vector <math>\overrightarrow{O\omega_B}</math> is <math>6</math> and is at a <math>30</math> degree angle from the horizontal. Therefore, the coordinates of this point are <math>(3\sqrt{3},3)</math> and by symmetry the coordinates of the center of <math>\omega_C</math> is <math>(-3\sqrt{3},3)</math>.
+
Note that <math>\triangle \omega_C E X</math> is an isosceles triangle, so <cmath>EX = 2 \sqrt{(\omega_C E)^2 - \left(\frac{\omega_B \omega_C}{2}\right)^2} = 2 \sqrt{r^2 - \left(\frac{\omega_B \omega_C}{2}\right)^2} = 2 \sqrt{12^2 - (3 \sqrt{3})^2} = 2 \sqrt{117}.</cmath>
  
−
The upper left and right circles intersect at two points, the lower of which is <math>X</math>. The equations of these two circles are:
+
<math>\textbf{Step 3:}</math>  
−
<cmath>(x+3\sqrt3)^2 + (y-3)^2 = 12^2</cmath>
 
−
<cmath>(x-3\sqrt3)^2 + (y-3)^2 = 12^2</cmath>
 
  
−
We solve this system by subtracting to get <math>x = 0</math>. Plugging back in to the first equation, we have <math>(3\sqrt{3})^2 + (y-3)^2 = 144 \implies (y-3)^2 = 117 \implies y-3 = \pm \sqrt{117} \implies y = 3 \pm \sqrt{117}</math>. Since we know <math>X</math> is the lower solution, we take the negative value to get <math>X = (0,3-\sqrt{117})</math>.
+
In <math>\odot \omega_C</math>, Power of a Point gives <math>\omega X \cdot \omega E = r^2 - (\omega_C \omega)^2</math> and <math>\omega E = EX - \omega X = 2\sqrt{117} - \omega X</math>.
  
−
We can solve the problem two ways from here. We can find <math>Y</math> by rotation and use the distance formula to find the length, or we can be somewhat more clever. We notice that it is easier to find <math>OX</math> as they lie on the same vertical, <math>\angle XOY</math> is <math>120</math> degrees so we can make use of <math>30-60-90</math> triangles, and <math>OX = OY</math> because <math>O</math> is the center of triangle <math>XYZ</math>. We can draw the diagram as such:
+
It follows that <math>\omega X \cdot (2\sqrt{117} - \omega X) = 12^2 - 6^2</math>. We solve this quadratic equation: <math>\omega X = \sqrt{117} - 3</math>.
  
−
<asy>
+
Since <math>\omega X</math> is the circumradius of equilateral <math>\triangle XYZ</math>, we have <math>XY = \sqrt{3} \cdot \omega X = \sqrt{3} \cdot (\sqrt{117} - 3) = \sqrt{351}-\sqrt{27}</math>.
−
unitsize(0.3cm);
 
−
draw(circle((0,0),18));
 
−
pair C = (9 * sqrt(3), -9);
 
−
pair B = (-9 * sqrt(3), -9);
 
−
pair B2 = (-12 * sqrt(3), -18);
 
−
pair C2 = (12 * sqrt(3), -18);
 
  
−
pair A = (0,18);
+
Therefore, the answer is <math>351+27 = \boxed{378}</math>.
−
draw(A--B--C--cycle);
 
−
draw(circle((0,-6),12), gray);
 
−
draw(circle((3*sqrt(3),3),12), gray);
 
−
draw(circle((-3*sqrt(3),3),12), gray);
 
  
−
draw(B--B2,dashed);
+
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
−
draw(C--C2,dashed);
 
−
draw(B2--C2,dashed);
 
  
−
dot(B2);
+
==Solution 3 (Simple Geometry)==
−
dot(C2);
+
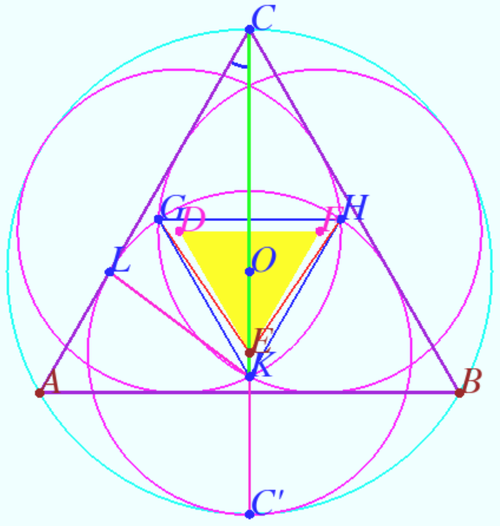
[[File:AIME 2022 I 7.png|500px|right]]
 +
Let <math>O</math> be the center, <math>R = 18</math> be the radius, and <math>CC'</math> be the diameter of <math>\omega.</math>
 +
Let <math>r</math>  be the radius, <math>E,D,F</math> are the centers of <math>\omega_A, \omega_B,\omega_C.</math>
 +
Let <math>KGH</math> be the desired triangle with side  <math>x.</math>
 +
We find <math>r</math> using
 +
<cmath>CC' = 2R = C'K + KC = r + \frac{r}{\sin 30^\circ} = 3r.</cmath>
 +
<cmath>r = \frac{2R}{3} = 12.</cmath>
 +
<cmath>OE = R – r = 6.</cmath>
 +
Triangles <math>\triangle DEF</math> and <math>\triangle KGH</math> – are equilateral triangles with a common center <math>O,</math> therefore in the triangle  <math>OEH</math> <math>OE = 6, \angle EOH = 120^\circ, OH = \frac{x}{\sqrt3}.</math>
 +
 +
We apply the Law of Cosines to <math>\triangle OEH</math> and get
 +
<cmath>OE^2 + OH^2 + OE \cdot OH = EH^2.</cmath>
 +
<cmath>6^2 + \frac{x^2}{3} + \frac{6x}{\sqrt3} = 12^2.</cmath>
 +
<cmath>x^2 + 6x \sqrt{3} = 324</cmath>
 +
<cmath>x= \sqrt{351} - \sqrt{27}  \implies 351 + 27 = \boxed {378}</cmath>
  
−
pair X = (0, 3-sqrt(117));
+
'''vladimir.shelomovskii@gmail.com, vvsss'''
−
pair Y = ( (sqrt(351)-sqrt(27))/2, (sqrt(117)-3)/2 );
 
−
pair Z = ( (sqrt(27) - sqrt(351))/2, (sqrt(117)-3)/2 );
 
−
dot(X);
 
−
dot(Y);
 
−
dot(Z);
 
−
dot((0,0));
 
−
label("$O$",(0,0),N);
 
  
−
label("$A$",A,N);
+
==Solution 4 (Mixtilinear Incircles)==
−
label("$B$",B,W);
+
Let <math>O</math> be the center of <math>\omega</math>, <math>X</math> be the intersection of <math>\omega_B,\omega_C</math> further from <math>A</math>, and <math>O_A</math> be the center of <math>\omega_A</math>. Define <math>Y, Z, O_B, O_C</math> similarly. It is well-known that the <math>A</math>-mixtilinear inradius <math>R_A</math> is <math>\tfrac{r}{\cos^2\left(\frac{\angle A}{2}\right)} = \tfrac{9}{\cos^2\left(30^{\circ}\right)} = 12</math>, so in particular this means that <math>OO_B = 18 -  R_B = 6 = OO_C</math>. Since <math>\angle O_BOO_C = \angle BOC = 120^\circ</math>, it follows by Law of Cosines on <math>\triangle OO_BO_C</math> that <math>O_BO_C = 6\sqrt{3}</math>. Then the Pythagorean theorem gives that the altitude of <math>O_BO_CX</math> is <math>\sqrt{117}</math>, so <math>OY = OX = \text{dist}(X, YZ) - \text{dist}(O, YZ) = \sqrt{117} - 3</math> and <math>YZ = \tfrac{O_BO_C\cdot OY}{OO_B} = \tfrac{6\sqrt{3}(\sqrt{117} - 3)}{6}=\sqrt{351} - \sqrt{27}</math> so the answer is <math>351 + 27 = \boxed{378}</math>.
−
label("$C$",C,E);
 
−
label("$B'$",B2,W);
 
−
label("$C'$",C2,E);
 
−
label("$X$",X,S);
 
−
label("$Y$",Y,E);
 
−
label("$Z$",Z,W);
 
  
−
draw(O--X);
+
~Kagebaka
−
draw(O--Y);
 
−
draw(O--((sqrt(351)-sqrt(27))/4,((sqrt(117)-3)/2 + (3-\sqrt{117}))/2));
 
  
 +
==Video Solution==
  
−
draw(X--Y--Z--cycle, dashed);
+
https://youtu.be/q6_LslAfFpI
−
</asy>
 
  
−
==Solution 2==
+
~MathProblemSolvingSkills.com
  
−
Let bottom left point as the origin, the radius of each circle is <math>36/3=12</math>, note that three centers for circles are <math>(9\sqrt{3},3),(12\sqrt{3},12),(6\sqrt{3},12)</math>
+
==Video Solution==
  
−
It is not hard to find that one intersection point lies on <math>\frac{\sqrt{3}x}{3}</math> since the intersection must lie on the angle bisector of the bigger triangle, plug it into equation
+
https://youtu.be/NTbdG4IiCRY
−
<math>(x-9\sqrt{3})^2+(\frac{\sqrt{3}x}{3}-3)^2=12^2</math>, getting that <math>x=\frac{15\sqrt{3}+3\sqrt{39}}{2}</math>, the length is <math>2*(\frac{15\sqrt{3}+3\sqrt{39}-18\sqrt{3}}{2}=3\sqrt{39}-3\sqrt{3}</math>, leads to the answer <math>378</math>
 
  
−
~bluesoul
+
~AMC & AIME Training
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2022|n=I|num-b=7|num-a=9}}
 
{{AIME box|year=2022|n=I|num-b=7|num-a=9}}
 +
 +
[[Category:Intermediate Geometry Problems]]
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 20:11, 31 January 2024

Problem

Equilateral triangle $\triangle ABC$ is inscribed in circle $\omega$ with radius $18.$ Circle $\omega_A$ is tangent to sides $\overline{AB}$ and $\overline{AC}$ and is internally tangent to $\omega.$ Circles $\omega_B$ and $\omega_C$ are defined analogously. Circles $\omega_A,$ $\omega_B,$ and $\omega_C$ meet in six points---two points for each pair of circles. The three intersection points closest to the vertices of $\triangle ABC$ are the vertices of a large equilateral triangle in the interior of $\triangle ABC,$ and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of $\triangle ABC.$ The side length of the smaller equilateral triangle can be written as $\sqrt{a} - \sqrt{b},$ where $a$ and $b$ are positive integers. Find $a+b.$

Diagram

[asy] /* Made by MRENTHUSIASM */ size(250); pair A, B, C, W, WA, WB, WC, X, Y, Z; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$\omega$",W,1.5*dir(270),linewidth(4)); dot("$\omega_A$",WA,1.5*dir(-WA),linewidth(4)); dot("$\omega_B$",WB,1.5*dir(-WB),linewidth(4)); dot("$\omega_C$",WC,1.5*dir(-WC),linewidth(4)); [/asy] ~MRENTHUSIASM ~ihatemath123

Solution 1 (Coordinate Geometry)

We can extend $AB$ and $AC$ to $B'$ and $C'$ respectively such that circle $\omega_A$ is the incircle of $\triangle AB'C'$. [asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, B1, C1, W, WA, WB, WC, X, Y, Z; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); B1 = A+24*sqrt(3)*dir(B-A); C1 = A+24*sqrt(3)*dir(C-A); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); draw(B--B1--C1--C,dashed); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*(-1,0),linewidth(4)); dot("$C$",C,1.5*(1,0),linewidth(4)); dot("$B'$",B1,1.5*dir(B1),linewidth(4)); dot("$C'$",C1,1.5*dir(C1),linewidth(4)); dot("$O$",W,1.5*dir(90),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); [/asy] Since the diameter of the circle is the height of this triangle, the height of this triangle is $36$. We can use inradius or equilateral triangle properties to get the inradius of this triangle is $12$ (The incenter is also a centroid in an equilateral triangle, and the distance from a side to the centroid is a third of the height). Therefore, the radius of each of the smaller circles is $12$.

Let $O=\omega$ be the center of the largest circle. We will set up a coordinate system with $O$ as the origin. The center of $\omega_A$ will be at $(0,-6)$ because it is directly beneath $O$ and is the length of the larger radius minus the smaller radius, or $18-12 = 6$. By rotating this point $120^{\circ}$ around $O$, we get the center of $\omega_B$. This means that the magnitude of vector $\overrightarrow{O\omega_B}$ is $6$ and is at a $30$ degree angle from the horizontal. Therefore, the coordinates of this point are $(3\sqrt{3},3)$ and by symmetry the coordinates of the center of $\omega_C$ is $(-3\sqrt{3},3)$.

The upper left and right circles intersect at two points, the lower of which is $X$. The equations of these two circles are: \begin{align*} (x+3\sqrt3)^2 + (y-3)^2 &= 12^2, \\ (x-3\sqrt3)^2 + (y-3)^2 &= 12^2. \end{align*} We solve this system by subtracting to get $x = 0$. Plugging back in to the first equation, we have $(3\sqrt{3})^2 + (y-3)^2 = 144 \implies (y-3)^2 = 117 \implies y-3 = \pm \sqrt{117} \implies y = 3 \pm \sqrt{117}$. Since we know $X$ is the lower solution, we take the negative value to get $X = (0,3-\sqrt{117})$.

We can solve the problem two ways from here. We can find $Y$ by rotation and use the distance formula to find the length, or we can be somewhat more clever. We notice that it is easier to find $OX$ as they lie on the same vertical, $\angle XOY$ is $120$ degrees so we can make use of $30-60-90$ triangles, and $OX = OY$ because $O$ is the center of triangle $XYZ$. We can draw the diagram as such: [asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, B1, C1, W, WA, WB, WC, X, Y, Z; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); B1 = A+24*sqrt(3)*dir(B-A); C1 = A+24*sqrt(3)*dir(C-A); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); draw(B--B1--C1--C^^W--X^^W--Y^^W--midpoint(X--Y),dashed); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*(-1,0),linewidth(4)); dot("$C$",C,1.5*(1,0),linewidth(4)); dot("$B'$",B1,1.5*dir(B1),linewidth(4)); dot("$C'$",C1,1.5*dir(C1),linewidth(4)); dot("$O$",W,1.5*dir(90),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); [/asy] Note that $OX = OY = \sqrt{117} - 3$. It follows that \begin{align*} XY &= 2 \cdot \frac{OX\cdot\sqrt{3}}{2} \\ &= OX \cdot \sqrt{3} \\ &= (\sqrt{117}-3) \cdot \sqrt{3} \\ &= \sqrt{351}-\sqrt{27}. \end{align*} Finally, the answer is $351+27 = \boxed{378}$.

~KingRavi

Solution 2 (Euclidean Geometry)

[asy] /* Made by MRENTHUSIASM */ /* Modified by isabelchen */ size(250); pair A, B, C, W, WA, WB, WC, X, Y, Z, D, E; A = 18*dir(90); B = 18*dir(210); C = 18*dir(330); W = (0,0); WA = 6*dir(270); WB = 6*dir(30); WC = 6*dir(150); X = (sqrt(117)-3)*dir(270); Y = (sqrt(117)-3)*dir(30); Z = (sqrt(117)-3)*dir(150); D = intersectionpoint(Circle(WA,12),A--C); E = intersectionpoints(Circle(WB,12),Circle(WC,12))[0]; filldraw(X--Y--Z--cycle,green,dashed); draw(Circle(WA,12)^^Circle(WB,12)^^Circle(WC,12),blue); draw(Circle(W,18)^^A--B--C--cycle); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$\omega$",W,1.5*dir(270),linewidth(4)); dot("$\omega_A$",WA,1.5*dir(-WA),linewidth(4)); dot("$\omega_B$",WB,1.5*dir(-WB),linewidth(4)); dot("$\omega_C$",WC,1.5*dir(-WC),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); dot("$E$",E,1.5*dir(E),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); draw(WC--WB^^WC--X^^WC--E^^WA--D^^A--X); [/asy] For equilateral triangle with side length $l$, height $h$, and circumradius $r$, there are relationships: $h = \frac{\sqrt{3}}{2} l$, $r = \frac{2}{3} h = \frac{\sqrt{3}}{3} l$, and $l = \sqrt{3}r$.

There is a lot of symmetry in the figure. The radius of the big circle $\odot \omega$ is $R = 18$, let the radius of the small circles $\odot \omega_A$, $\odot \omega_B$, $\odot \omega_C$ be $r$.

We are going to solve this problem in $3$ steps:

$\textbf{Step 1:}$

We have $\triangle A \omega_A D$ is a $30-60-90$ triangle, and $A \omega_A = 2 \cdot \omega_A D$, $A \omega_A = 2R-r$ ($\odot \omega$ and $\odot \omega_A$ are tangent), and $\omega_A D = r$. So, we get $2R-r = 2r$ and $r = \frac{2}{3} \cdot R = 12$.

Since $\odot \omega$ and $\odot \omega_A$ are tangent, we get $\omega \omega_A = R - r = \frac{1}{3} \cdot R = 6$.

Note that $\triangle \omega_A \omega_B \omega_C$ is an equilateral triangle, and $\omega$ is its center, so $\omega_B \omega_C = \sqrt{3} \cdot \omega \omega_A = 6 \sqrt{3}$.

$\textbf{Step 2:}$

Note that $\triangle \omega_C E X$ is an isosceles triangle, so \[EX = 2 \sqrt{(\omega_C E)^2 - \left(\frac{\omega_B \omega_C}{2}\right)^2} = 2 \sqrt{r^2 - \left(\frac{\omega_B \omega_C}{2}\right)^2} = 2 \sqrt{12^2 - (3 \sqrt{3})^2} = 2 \sqrt{117}.\]

$\textbf{Step 3:}$

In $\odot \omega_C$, Power of a Point gives $\omega X \cdot \omega E = r^2 - (\omega_C \omega)^2$ and $\omega E = EX - \omega X = 2\sqrt{117} - \omega X$.

It follows that $\omega X \cdot (2\sqrt{117} - \omega X) = 12^2 - 6^2$. We solve this quadratic equation: $\omega X = \sqrt{117} - 3$.

Since $\omega X$ is the circumradius of equilateral $\triangle XYZ$, we have $XY = \sqrt{3} \cdot \omega X = \sqrt{3} \cdot (\sqrt{117} - 3) = \sqrt{351}-\sqrt{27}$.

Therefore, the answer is $351+27 = \boxed{378}$.

~isabelchen

Solution 3 (Simple Geometry)

AIME 2022 I 7.png

Let $O$ be the center, $R = 18$ be the radius, and $CC'$ be the diameter of $\omega.$ Let $r$ be the radius, $E,D,F$ are the centers of $\omega_A, \omega_B,\omega_C.$ Let $KGH$ be the desired triangle with side $x.$ We find $r$ using \[CC' = 2R = C'K + KC = r + \frac{r}{\sin 30^\circ} = 3r.\] \[r = \frac{2R}{3} = 12.\] \[OE = R – r = 6.\] Triangles $\triangle DEF$ and $\triangle KGH$ – are equilateral triangles with a common center $O,$ therefore in the triangle $OEH$ $OE = 6, \angle EOH = 120^\circ, OH = \frac{x}{\sqrt3}.$

We apply the Law of Cosines to $\triangle OEH$ and get \[OE^2 + OH^2 + OE \cdot OH = EH^2.\] \[6^2 + \frac{x^2}{3} + \frac{6x}{\sqrt3} = 12^2.\] \[x^2 + 6x \sqrt{3} = 324\] \[x= \sqrt{351} - \sqrt{27} \implies 351 + 27 = \boxed {378}\]

vladimir.shelomovskii@gmail.com, vvsss

Solution 4 (Mixtilinear Incircles)

Let $O$ be the center of $\omega$, $X$ be the intersection of $\omega_B,\omega_C$ further from $A$, and $O_A$ be the center of $\omega_A$. Define $Y, Z, O_B, O_C$ similarly. It is well-known that the $A$-mixtilinear inradius $R_A$ is $\tfrac{r}{\cos^2\left(\frac{\angle A}{2}\right)} = \tfrac{9}{\cos^2\left(30^{\circ}\right)} = 12$, so in particular this means that $OO_B = 18 - R_B = 6 = OO_C$. Since $\angle O_BOO_C = \angle BOC = 120^\circ$, it follows by Law of Cosines on $\triangle OO_BO_C$ that $O_BO_C = 6\sqrt{3}$. Then the Pythagorean theorem gives that the altitude of $O_BO_CX$ is $\sqrt{117}$, so $OY = OX = \text{dist}(X, YZ) - \text{dist}(O, YZ) = \sqrt{117} - 3$ and $YZ = \tfrac{O_BO_C\cdot OY}{OO_B} = \tfrac{6\sqrt{3}(\sqrt{117} - 3)}{6}=\sqrt{351} - \sqrt{27}$ so the answer is $351 + 27 = \boxed{378}$.

~Kagebaka

Video Solution

https://youtu.be/q6_LslAfFpI

~MathProblemSolvingSkills.com

Video Solution

https://youtu.be/NTbdG4IiCRY

~AMC & AIME Training

See Also

2022 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 7 		Followed by
Problem 9
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_I_Problems/Problem_8&oldid=213992"