Difference between revisions of "2022 AIME I Problems/Problem 15"
Pi is 3.14 (talk | contribs) (→Solution 2 (Detailed Geometric Solution created by ChatGPT)) |
(→Solution 5) |
||
| (44 intermediate revisions by 7 users not shown) | |||
| Line 10: | Line 10: | ||
==Solution 1 (geometric interpretation)== | ==Solution 1 (geometric interpretation)== | ||
| − | First, | + | First, let define a triangle with side lengths <math>\sqrt{2x}</math>, <math>\sqrt{2z}</math>, and <math>l</math>, with altitude from <math>l</math>'s equal to <math>\sqrt{xz}</math>. <math>l = \sqrt{2x - xz} + \sqrt{2z - xz}</math>, the left side of one equation in the problem. |
| − | + | Let <math>\theta</math> be angle opposite the side with length <math>\sqrt{2x}</math>. Then the altitude has length <math>\sqrt{2z} \cdot \sin(\theta) = \sqrt{xz}</math> and thus <math>\sin(\theta) = \sqrt{\frac{x}{2}}</math>, so <math>x=2\sin^2(\theta)</math> and the side length <math>\sqrt{2x}</math> is equal to <math>2\sin(\theta)</math>. | |
| − | We | + | We can symmetrically apply this to the two other equations/triangles. |
| − | + | By law of sines, we have <math>\frac{2\sin(\theta)}{\sin(\theta)} = 2R</math>, with <math>R=1</math> as the circumradius, same for all 3 triangles. | |
| + | The circumcircle's central angle to a side is <math>2 \arcsin(l/2)</math>, so the 3 triangles' <math>l=1, \sqrt{2}, \sqrt{3}</math>, have angles <math>120^{\circ}, 90^{\circ}, 60^{\circ}</math>, respectively. | ||
| − | == | + | This means that by half angle arcs, we see that we have in some order, <math>x=2\sin^2(\alpha)</math>, <math>y=2\sin^2(\beta)</math>, and <math>z=2\sin^2(\gamma)</math> (not necessarily this order, but here it does not matter due to symmetry), satisfying that <math>\alpha+\beta=180^{\circ}-\frac{120^{\circ}}{2}</math>, <math>\beta+\gamma=180^{\circ}-\frac{90^{\circ}}{2}</math>, and <math>\gamma+\alpha=180^{\circ}-\frac{60^{\circ}}{2}</math>. Solving, we get <math>\alpha=\frac{135^{\circ}}{2}</math>, <math>\beta=\frac{105^{\circ}}{2}</math>, and <math>\gamma=\frac{165^{\circ}}{2}</math>. |
| − | + | We notice that <cmath>[(1-x)(1-y)(1-z)]^2=[\sin(2\alpha)\sin(2\beta)\sin(2\gamma)]^2=[\sin(135^{\circ})\sin(105^{\circ})\sin(165^{\circ})]^2</cmath> <cmath>=\left(\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{6}-\sqrt{2}}{4} \cdot \frac{\sqrt{6}+\sqrt{2}}{4}\right)^2 = \left(\frac{\sqrt{2}}{8}\right)^2=\frac{1}{32} \to \boxed{033}. \blacksquare</cmath> | |
| − | + | - kevinmathz | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Solution 2 (pure algebraic trig, easy to follow)== | ==Solution 2 (pure algebraic trig, easy to follow)== | ||
| Line 69: | Line 34: | ||
\sqrt{z}\cdot\sqrt{2-x} + \sqrt{x}\cdot\sqrt{2-z} &= \sqrt3. | \sqrt{z}\cdot\sqrt{2-x} + \sqrt{x}\cdot\sqrt{2-z} &= \sqrt3. | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| + | |||
This should give off tons of trigonometry vibes. To make the connection clear, <math>x = 2\cos^2 \alpha</math>, <math>y = 2\cos^2 \beta</math>, and <math>z = 2\cos^2 \theta</math> is a helpful substitution: | This should give off tons of trigonometry vibes. To make the connection clear, <math>x = 2\cos^2 \alpha</math>, <math>y = 2\cos^2 \beta</math>, and <math>z = 2\cos^2 \theta</math> is a helpful substitution: | ||
| + | |||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
\sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \beta} + \sqrt{2\cos^2 \beta}\cdot\sqrt{2-2\cos^2 \alpha} &= 1 \\ | \sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \beta} + \sqrt{2\cos^2 \beta}\cdot\sqrt{2-2\cos^2 \alpha} &= 1 \\ | ||
| Line 75: | Line 42: | ||
\sqrt{2\cos^2 \theta}\cdot\sqrt{2-2\cos^2 \alpha} + \sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \theta} &= \sqrt3. | \sqrt{2\cos^2 \theta}\cdot\sqrt{2-2\cos^2 \alpha} + \sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \theta} &= \sqrt3. | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| + | |||
From each equation <math>\sqrt{2}^2</math> can be factored out, and when every equation is divided by 2, we get: | From each equation <math>\sqrt{2}^2</math> can be factored out, and when every equation is divided by 2, we get: | ||
| + | |||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
\sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \beta} + \sqrt{\cos^2 \beta}\cdot\sqrt{1-\cos^2 \alpha} &= \frac{1}{2} \\ | \sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \beta} + \sqrt{\cos^2 \beta}\cdot\sqrt{1-\cos^2 \alpha} &= \frac{1}{2} \\ | ||
| Line 81: | Line 50: | ||
\sqrt{\cos^2 \theta}\cdot\sqrt{1-\cos^2 \alpha} + \sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \theta} &= \frac{\sqrt3}{2}. | \sqrt{\cos^2 \theta}\cdot\sqrt{1-\cos^2 \alpha} + \sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \theta} &= \frac{\sqrt3}{2}. | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| + | |||
which simplifies to (using the Pythagorean identity <math>\sin^2 \phi + \cos^2 \phi = 1 \; \forall \; \phi \in \mathbb{C} </math>): | which simplifies to (using the Pythagorean identity <math>\sin^2 \phi + \cos^2 \phi = 1 \; \forall \; \phi \in \mathbb{C} </math>): | ||
| + | |||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
\cos \alpha\cdot\sin \beta + \cos \beta\cdot\sin \alpha &= \frac{1}{2} \\ | \cos \alpha\cdot\sin \beta + \cos \beta\cdot\sin \alpha &= \frac{1}{2} \\ | ||
| Line 87: | Line 58: | ||
\cos \theta\cdot\sin \alpha + \cos \alpha\cdot\sin \theta &= \frac{\sqrt3}{2}. | \cos \theta\cdot\sin \alpha + \cos \alpha\cdot\sin \theta &= \frac{\sqrt3}{2}. | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| + | |||
which further simplifies to (using sine addition formula <math>\sin(a + b) = \sin a \cos b + \cos a \sin b</math>): | which further simplifies to (using sine addition formula <math>\sin(a + b) = \sin a \cos b + \cos a \sin b</math>): | ||
| + | |||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
\sin(\alpha + \beta) &= \frac{1}{2} \\ | \sin(\alpha + \beta) &= \frac{1}{2} \\ | ||
| Line 93: | Line 66: | ||
\sin(\alpha + \theta) &= \frac{\sqrt3}{2}. | \sin(\alpha + \theta) &= \frac{\sqrt3}{2}. | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| − | + | ||
| + | Taking the inverse sine (<math>0\leq\theta\frac{\pi}{2}</math>) of each equation yields a simple system: | ||
| + | |||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
\alpha + \beta &= \frac{\pi}{6} \\ | \alpha + \beta &= \frac{\pi}{6} \\ | ||
\beta + \theta &= \frac{\pi}{4} \\ | \beta + \theta &= \frac{\pi}{4} \\ | ||
| − | \alpha + \theta &= \frac{\pi}{3} | + | \alpha + \theta &= \frac{\pi}{3} |
| + | \end{align*}</cmath> | ||
| + | |||
| + | giving solutions: | ||
| + | |||
| + | <cmath>\begin{align*} | ||
| + | \alpha &= \frac{\pi}{8} \\ | ||
| + | \beta &= \frac{\pi}{24} \\ | ||
| + | \theta &= \frac{5\pi}{24} | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| − | + | ||
| − | <cmath>\left[ (-1)^3\left(\cos \left(2\cdot\frac{\pi}{8}\right)\cos \left(2\cdot\frac{\pi}{24}\right)\cos \left(2\cdot\frac{5\pi}{24}\right)\right)\right]^2 = \left[ (-1)\left(\cos \left(\frac{\pi}{4}\right)\cos \left(\frac{\pi}{12}\right)\cos \left(\frac{5\pi}{12}\right)\right)\right]^2 </cmath> | + | Since these unknowns are directly related to our original unknowns, there are consequent solutions for those: |
| − | Now, all the cosines in here are fairly standard: < | + | |
| − | <cmath>(-1)^2\left(\frac{\sqrt{2}}{2}\right)^2\left(\frac{\sqrt{6} + \sqrt{2}}{4}\right)^2\left(\frac{\sqrt{6} - \sqrt{2}}{4}\right)^2 = \left(\frac{1}{2}\right)\left(\frac{ | + | |
| − | This is our answer in simplest form <math>\frac{m}{n}</math>, so <math>m + n = 1 + 32 = \boxed{033} | + | <cmath>\begin{align*} |
| + | x &= 2\cos^2\left(\frac{\pi}{8}\right) \\ | ||
| + | y &= 2\cos^2\left(\frac{\pi}{24}\right) \\ | ||
| + | z &= 2\cos^2\left(\frac{5\pi}{24}\right) | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | When plugging into the expression <math>\left[ (1-x)(1-y)(1-z) \right]^2</math>, noting that <math>-\cos 2\phi = 1 - 2\cos^2 \phi\; \forall \; \phi \in \mathbb{C}</math> helps to simplify this expression into: | ||
| + | |||
| + | |||
| + | <cmath>\begin{align*} | ||
| + | \left[ (-1)^3\left(\cos \left(2\cdot\frac{\pi}{8}\right)\cos \left(2\cdot\frac{\pi}{24}\right)\cos \left(2\cdot\frac{5\pi}{24}\right)\right)\right]^2 \\ | ||
| + | = \left[ (-1)\left(\cos \left(\frac{\pi}{4}\right)\cos \left(\frac{\pi}{12}\right)\cos \left(\frac{5\pi}{12}\right)\right)\right]^2 | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | Now, all the cosines in here are fairly standard: | ||
| + | |||
| + | <cmath>\begin{align*} | ||
| + | \cos \frac{\pi}{4} &= \frac{\sqrt{2}}{2} \\ | ||
| + | \cos \frac{\pi}{12} &=\frac{\sqrt{6} + \sqrt{2}}{4} & (= \cos{\frac{\frac{\pi}{6}}{2}} ) \\ | ||
| + | \cos \frac{5\pi}{12} &= \frac{\sqrt{6} - \sqrt{2}}{4} & (= \cos\left({\frac{\pi}{6} + \frac{\pi}{4}} \right) ) | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | With some final calculations: | ||
| + | |||
| + | |||
| + | <cmath>\begin{align*} | ||
| + | &(-1)^2\left(\frac{\sqrt{2}}{2}\right)^2\left(\frac{\sqrt{6} + \sqrt{2}}{4}\right)^2\left(\frac{\sqrt{6} - \sqrt{2}}{4}\right)^2 \\ | ||
| + | =& | ||
| + | \left(\frac{1}{2}\right) | ||
| + | \left(\left(\frac{\sqrt{6} + \sqrt{2}}{4}\right)\left(\frac{\sqrt{6} - \sqrt{2}}{4}\right)\right)^2 \\ | ||
| + | =&\frac{1}{2} \frac{4^2}{16^2} = \frac{1}{32} | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | This is our answer in simplest form <math>\frac{m}{n}</math>, so <math>m + n = 1 + 32 = \boxed{033}</math>. | ||
~Oxymoronic15 | ~Oxymoronic15 | ||
| − | == | + | ==Solution 3 (substitution)== |
Let <math>1-x=a;1-y=b;1-z=c</math>, rewrite those equations | Let <math>1-x=a;1-y=b;1-z=c</math>, rewrite those equations | ||
| Line 116: | Line 132: | ||
<math>\sqrt{(1-a)(1+c)}+\sqrt{(1-c)(1+a)}=\sqrt{3}</math> | <math>\sqrt{(1-a)(1+c)}+\sqrt{(1-c)(1+a)}=\sqrt{3}</math> | ||
| − | + | and solve for <math>m/n = (abc)^2 = a^2b^2c^2</math> | |
| + | |||
| + | Square both sides and simplify, to get three equations: | ||
<math>2ab-1=2\sqrt{(1-a^2)(1-b^2)}</math> | <math>2ab-1=2\sqrt{(1-a^2)(1-b^2)}</math> | ||
| − | <math>2bc=2\sqrt{(1-b^2)(1-c^2)}</math> | + | <math>2bc~ ~ ~ ~ ~ ~=2\sqrt{(1-b^2)(1-c^2)}</math> |
<math>2ac+1=2\sqrt{(1-c^2)(1-a^2)}</math> | <math>2ac+1=2\sqrt{(1-c^2)(1-a^2)}</math> | ||
| − | + | Square both sides again, and simplify to get three equations: | |
| + | |||
| + | <math>a^2+b^2-ab=\frac{3}{4}</math> | ||
| − | <math>b^2+c^2=1</math> | + | <math>b^2+c^2~ ~ ~ ~ ~ ~=1</math> |
<math>a^2+c^2+ac=\frac{3}{4}</math> | <math>a^2+c^2+ac=\frac{3}{4}</math> | ||
| Line 134: | Line 154: | ||
Put it in first equation, getting <math>b^2-2bc+c^2+b^2-b(b-c)=b^2+c^2-bc=\frac{3}{4}</math>, <math>bc=\frac{1}{4}</math> | Put it in first equation, getting <math>b^2-2bc+c^2+b^2-b(b-c)=b^2+c^2-bc=\frac{3}{4}</math>, <math>bc=\frac{1}{4}</math> | ||
| − | Since <math>a^2=b^2+c^2-2bc=\frac{1}{2}</math>, | + | Since <math>a^2=b^2+c^2-2bc=\frac{1}{2}</math>, <math>m/n = a^2b^2c^2 = a^2(bc)^2 = \frac{1}{2}\left(\frac{1}{4}\right)^2=\frac{1}{32}</math> and so the final answer is <math>\boxed{033}</math> |
~bluesoul | ~bluesoul | ||
| Line 256: | Line 276: | ||
Therefore, the answer is <math>1 + 32 = \boxed{\textbf{(033) }}</math>. | Therefore, the answer is <math>1 + 32 = \boxed{\textbf{(033) }}</math>. | ||
| − | |||
~Steven Chen (www.professorchenedu.com) | ~Steven Chen (www.professorchenedu.com) | ||
| − | + | bu-bye | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
\sin(\alpha + \beta) &= 1/2 \\ | \sin(\alpha + \beta) &= 1/2 \\ | ||
| Line 310: | Line 320: | ||
\angle Y'OY = \angle Y'OZ + \angle YOZ = 45^\circ + 30 ^\circ = 75^\circ.</math> | \angle Y'OY = \angle Y'OZ + \angle YOZ = 45^\circ + 30 ^\circ = 75^\circ.</math> | ||
| − | Points <math>Y</math> and <math>Y'</math> are | + | Points <math>Y</math> and <math>Y'</math> are symmetric with respect to <math>OM.</math> |
<i><b>Case 1</b></i> | <i><b>Case 1</b></i> | ||
| Line 323: | Line 333: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/i6kDMbav2sk | ||
| + | |||
| + | ~Math Gold Medalist | ||
| + | |||
| + | |||
| + | ==Video Solution== | ||
| + | |||
| + | https://youtu.be/aa_VY4e4OOM?si=1lHSwY3v7RICoEpk | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
| + | |||
| + | |||
==Video Solution== | ==Video Solution== | ||
Latest revision as of 00:25, 1 February 2024
Contents
Problem
Let ![]()
![]() and
and ![]() be positive real numbers satisfying the system of equations:
be positive real numbers satisfying the system of equations:
 Then
Then ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Solution 1 (geometric interpretation)
First, let define a triangle with side lengths ![]() ,
, ![]() , and
, and ![]() , with altitude from
, with altitude from ![]() 's equal to
's equal to ![]() .
. ![]() , the left side of one equation in the problem.
, the left side of one equation in the problem.
Let ![]() be angle opposite the side with length
be angle opposite the side with length ![]() . Then the altitude has length
. Then the altitude has length ![]() and thus
and thus ![]() , so
, so ![]() and the side length
and the side length ![]() is equal to
is equal to ![]() .
.
We can symmetrically apply this to the two other equations/triangles.
By law of sines, we have ![]() , with
, with ![]() as the circumradius, same for all 3 triangles.
The circumcircle's central angle to a side is
as the circumradius, same for all 3 triangles.
The circumcircle's central angle to a side is ![]() , so the 3 triangles'
, so the 3 triangles' ![]() , have angles
, have angles ![]() , respectively.
, respectively.
This means that by half angle arcs, we see that we have in some order, ![]() ,
, ![]() , and
, and ![]() (not necessarily this order, but here it does not matter due to symmetry), satisfying that
(not necessarily this order, but here it does not matter due to symmetry), satisfying that ![]() ,
, ![]() , and
, and ![]() . Solving, we get
. Solving, we get ![]() ,
, ![]() , and
, and ![]() .
.
We notice that ![]()
![\[=\left(\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{6}-\sqrt{2}}{4} \cdot \frac{\sqrt{6}+\sqrt{2}}{4}\right)^2 = \left(\frac{\sqrt{2}}{8}\right)^2=\frac{1}{32} \to \boxed{033}. \blacksquare\]](http://latex.artofproblemsolving.com/4/8/0/4806ad451d0248129d657ed966100bf612900876.png)
- kevinmathz
Solution 2 (pure algebraic trig, easy to follow)
(This eventually whittles down to the same concept as Solution 1)
Note that in each equation in this system, it is possible to factor ![]() ,
, ![]() , or
, or ![]() from each term (on the left sides), since each of
from each term (on the left sides), since each of ![]() ,
, ![]() , and
, and ![]() are positive real numbers. After factoring out accordingly from each terms one of
are positive real numbers. After factoring out accordingly from each terms one of ![]() ,
, ![]() , or
, or ![]() , the system should look like this:
, the system should look like this:

This should give off tons of trigonometry vibes. To make the connection clear, ![]() ,
, ![]() , and
, and ![]() is a helpful substitution:
is a helpful substitution:

From each equation ![]() can be factored out, and when every equation is divided by 2, we get:
can be factored out, and when every equation is divided by 2, we get:

which simplifies to (using the Pythagorean identity ![]() ):
):

which further simplifies to (using sine addition formula ![]() ):
):

Taking the inverse sine (![]() ) of each equation yields a simple system:
) of each equation yields a simple system:

giving solutions:

Since these unknowns are directly related to our original unknowns, there are consequent solutions for those:

When plugging into the expression ![]() , noting that
, noting that ![]() helps to simplify this expression into:
helps to simplify this expression into:
![\begin{align*} \left[ (-1)^3\left(\cos \left(2\cdot\frac{\pi}{8}\right)\cos \left(2\cdot\frac{\pi}{24}\right)\cos \left(2\cdot\frac{5\pi}{24}\right)\right)\right]^2 \\ = \left[ (-1)\left(\cos \left(\frac{\pi}{4}\right)\cos \left(\frac{\pi}{12}\right)\cos \left(\frac{5\pi}{12}\right)\right)\right]^2 \end{align*}](http://latex.artofproblemsolving.com/6/1/b/61bbfe7cdbd936703304a9528a47e0c492f62811.png)
Now, all the cosines in here are fairly standard:

With some final calculations:

This is our answer in simplest form ![]() , so
, so ![]() .
.
~Oxymoronic15
Solution 3 (substitution)
Let ![]() , rewrite those equations
, rewrite those equations
![]() ;
;
![]()
![]()
and solve for ![]()
Square both sides and simplify, to get three equations:
![]()
![]()
![]()
Square both sides again, and simplify to get three equations:
![]()
![]()
![]()
Subtract first and third equation, getting ![]() ,
, ![]()
Put it in first equation, getting ![]() ,
, ![]()
Since ![]() ,
, ![]() and so the final answer is
and so the final answer is ![]()
~bluesoul
Solution 4
Denote ![]() ,
, ![]() ,
, ![]() .
Hence, the system of equations given in the problem can be written as
.
Hence, the system of equations given in the problem can be written as

Each equation above takes the following form:
![]()
Now, we simplify this equation by removing radicals.
Denote ![]() and
and ![]() .
.
Hence, the equation above implies
![\[ \left\{ \begin{array}{l} p + q = k \\ p^2 = (1-a)(1+b) \\ q^2 = (1+a)(1-b) \end{array} \right.. \]](http://latex.artofproblemsolving.com/4/b/e/4bed99ded09196ed2868510a10f5733e88189934.png)
Hence, ![]() .
Hence,
.
Hence, ![]() .
.
Because ![]() and
and ![]() , we get
, we get ![]() .
Plugging this into the equation
.
Plugging this into the equation ![]() and simplifying it, we get
and simplifying it, we get
![]()
Therefore, the system of equations above can be simplified as

Denote ![]() .
The system of equations above can be equivalently written as
.
The system of equations above can be equivalently written as

Taking ![]() , we get
, we get
![]()
Thus, we have either ![]() or
or ![]() .
.
![]() :
: ![]() .
.
Equation (2') implies ![]() .
.
Plugging ![]() and
and ![]() into Equation (2), we get contradiction. Therefore, this case is infeasible.
into Equation (2), we get contradiction. Therefore, this case is infeasible.
![]() :
: ![]() .
.
Plugging this condition into (1') to substitute ![]() , we get
, we get
![]()
Taking ![]() , we get
, we get
![]()
Taking (4) + (5), we get
![]()
Hence, ![]() .
.
Therefore,
![\begin{align*} \left[ (1-x)(1-y)(1-z) \right]^2 & = u^2 (vw)^2 \\ & = u^2 (vw')^2 \\ & = \frac{1}{2} \left( - \frac{1}{4} \right)^2 \\ & = \frac{1}{32} . \end{align*}](http://latex.artofproblemsolving.com/b/7/e/b7ecd3c2e3fd3f14f21546db474f4dc420c959ab.png)
Therefore, the answer is ![]() .
.
~Steven Chen (www.professorchenedu.com)
bu-bye
 Thus,
Thus,
 so
so ![]() . Hence,
. Hence,
![]() so
so ![]() , for a final answer of
, for a final answer of ![]() .
.
Remark
The motivation for the trig substitution is that if ![]() , then
, then ![]() , and when making the substitution in each equation of the initial set of equations, we obtain a new equation in the form of the sine addition formula.
, and when making the substitution in each equation of the initial set of equations, we obtain a new equation in the form of the sine addition formula.
~ Leo.Euler
Solution 6 (Geometric)
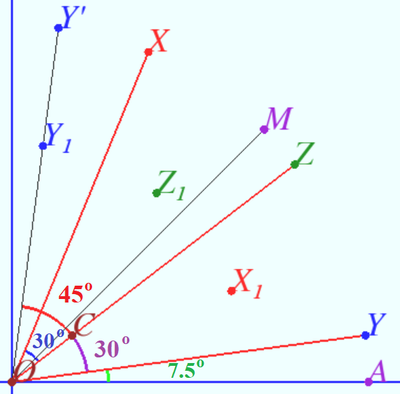
In given equations, ![]() so we define some points:
so we define some points:
![]()
![]()
![]() Notice, that
Notice, that ![]() and each points lies in the first quadrant.
and each points lies in the first quadrant.
We use given equations and get some scalar products:
![]()
![]()
![]() So
So ![]()
Points ![]() and
and ![]() are symmetric with respect to
are symmetric with respect to ![]()
Case 1
![]()
![]()
![]()
![]() Case 2
Case 2
![]()
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
~Math Gold Medalist
Video Solution
https://youtu.be/aa_VY4e4OOM?si=1lHSwY3v7RICoEpk
~MathProblemSolvingSkills.com
Video Solution
https://www.youtube.com/watch?v=ihKUZ5itcdA
~Steven Chen (www.professorchenedu.com)
See Also
| 2022 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.