Difference between revisions of "2023 AMC 12B Problems/Problem 10"
(→Solution 2 (Coordinate Geometry)) |
|||
| (12 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ==Solution== | + | ==Problem== |
| + | In the <math>xy</math>-plane, a circle of radius <math>4</math> with center on the positive <math>x</math>-axis is tangent to the <math>y</math>-axis at the origin, and a circle with radius <math>10</math> with center on the positive <math>y</math>-axis is tangent to the <math>x</math>-axis at the origin. What is the slope of the line passing through the two points at which these circles intersect? | ||
| + | |||
| + | <math>\textbf{(A)}\ \dfrac{2}{7} \qquad\textbf{(B)}\ \dfrac{3}{7} \qquad\textbf{(C)}\ \dfrac{2}{\sqrt{29}} \qquad\textbf{(D)}\ \dfrac{1}{\sqrt{29}} \qquad\textbf{(E)}\ \dfrac{2}{5}</math> | ||
| + | |||
| + | ==Solution 1== | ||
The center of the first circle is <math>(4,0)</math>. | The center of the first circle is <math>(4,0)</math>. | ||
| Line 6: | Line 11: | ||
Because this line is the perpendicular bisector of the line that passes through two intersecting points of two circles, the slope of the latter line is <math>\frac{-1}{- \frac{5}{2}} = \boxed{\textbf{(E) } \frac{2}{5}}</math>. | Because this line is the perpendicular bisector of the line that passes through two intersecting points of two circles, the slope of the latter line is <math>\frac{-1}{- \frac{5}{2}} = \boxed{\textbf{(E) } \frac{2}{5}}</math>. | ||
| + | |||
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ||
| + | |||
| + | ==Solution 2 (Coordinate Geometry)== | ||
| + | |||
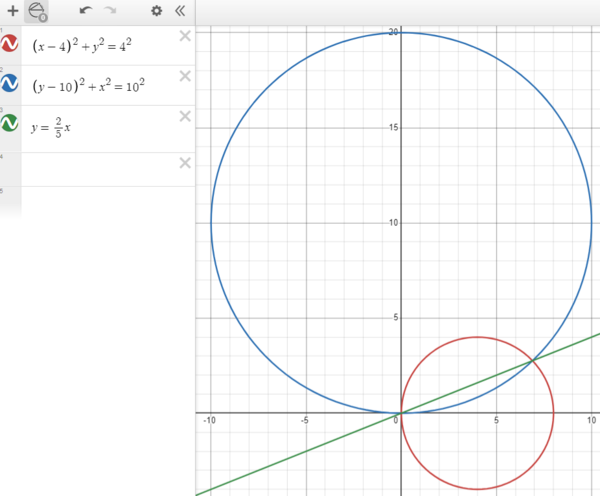
| + | The first circle can be written as <math>(x-4)^2 + y^2 = 4^2</math> we'll call this equation <math>(1)</math> | ||
| + | The second can we writen as <math>x^2 + (y-10)^2 = 10^2</math>, we'll call this equation <math>(2)</math> | ||
| + | |||
| + | Expanding <math>(1)</math>: | ||
| + | <cmath>\begin{align*} | ||
| + | x^2 -8x + 4^2 + y^2 &= 4^2 \\ | ||
| + | x^2 - 8x + y^2 &= 0 | ||
| + | \end{align*}</cmath> | ||
| + | Exapnding <math>(2)</math> | ||
| + | <cmath>\begin{align*} | ||
| + | x^2 + y^2 -20y + 10^2 = 10^2\\ | ||
| + | x^2 + y^2 - 20y = 0 | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | Now we can set the equations equal to eachother: | ||
| + | <cmath>\begin{align*} | ||
| + | x^2 - 8x + y^2 &= x^2 + y^2 - 20y \\ | ||
| + | \frac{8}{20}x &= y \\ | ||
| + | \frac{2}{5}x &= y | ||
| + | \end{align*}</cmath> | ||
| + | This is in slope intercept form therefore the slope is <math>\boxed{\textbf{(E) } \frac{2}{5}}</math>. | ||
| + | [[Image:Amc12B_2023_P10.PNG|thumb|center|600px]] | ||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso] | ||
| + | |||
| + | ==Video Solution 1 by OmegaLearn== | ||
| + | https://youtu.be/IUB6r1iNgpU | ||
| + | |||
| + | |||
| + | So um you can write both circles in polar form: The first circle with radius 4 um *long pause can be rewritten as r=8cosθ. And the other circle can be written as r=20sinθ. At the point of intersection, both radii will be equal. We can then do 8cosθ=20sinθ *clears throat. Rearrange the equation to solve for tanθ so tanθ = 2/5. Tanθ = y/x which yields the slope, so the slope is 2/5 <math>\boxed{\textbf{(E) } \frac{2}{5}}</math> moomoo. Thechickenonfire is the moomoo cow and you should milk the cow of knowledge. | ||
| + | |||
| + | |||
| + | -By Elite_Trash777 | ||
| + | |||
| + | ==Video Solution== | ||
| + | |||
| + | https://youtu.be/sjJMWtL_CEY | ||
| + | |||
| + | ~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC12 box|year=2023|ab=B|num-b=9|num-a=11}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 11:54, 17 August 2024
Contents
Problem
In the 
-plane, a circle of radius 
with center on the positive 
-axis is tangent to the 
-axis at the origin, and a circle with radius 
with center on the positive -axis is tangent to the -axis at the origin. What is the slope of the line passing through the two points at which these circles intersect?
Solution 1
The center of the first circle is 
.
The center of the second circle is 
.
Thus, the slope of the line that passes through these two centers is 
.
Because this line is the perpendicular bisector of the line that passes through two intersecting points of two circles, the slope of the latter line is 
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 2 (Coordinate Geometry)
The first circle can be written as 
we'll call this equation 
The second can we writen as 
, we'll call this equation 
Expanding :
Exapnding
Now we can set the equations equal to eachother:
This is in slope intercept form therefore the slope is 
.
Video Solution 1 by OmegaLearn
So um you can write both circles in polar form: The first circle with radius 4 um *long pause can be rewritten as r=8cosθ. And the other circle can be written as r=20sinθ. At the point of intersection, both radii will be equal. We can then do 8cosθ=20sinθ *clears throat. Rearrange the equation to solve for tanθ so tanθ = 2/5. Tanθ = y/x which yields the slope, so the slope is 2/5 moomoo. Thechickenonfire is the moomoo cow and you should milk the cow of knowledge.
-By Elite_Trash777
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
See Also
| 2023 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 9 |
Followed by Problem 11 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
