Difference between revisions of "2004 AMC 12B Problems/Problem 21"
(→See also) |
m (→Solution) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 15: | Line 15: | ||
Rearranging by the degree of <math>x</math>, | Rearranging by the degree of <math>x</math>, | ||
<cmath>(3m^2 + m + 2)x^2 - (20m + 11)x + 40 = 0</cmath> | <cmath>(3m^2 + m + 2)x^2 - (20m + 11)x + 40 = 0</cmath> | ||
| − | Since the line <math>y=mx</math>, we want the discriminant, | + | Since the line <math>y=mx</math> is tangent to the ellipse, we want the discriminant, |
| − | <cmath>(20m+11)^2 - 4\cdot 40 \cdot (3m^2 + m + 2) = -80m^2 + 280m - 199 | + | <cmath>(20m+11)^2 - 4\cdot 40 \cdot (3m^2 + m + 2) = -80m^2 + 280m - 199 </cmath> |
to be equal to <math>0</math>. We want <math>a+b</math>, which is the sum of the roots of the above quadratic. By [[Vieta’s formulas]], that is <math>\frac{280}{80} = \frac{7}{2} \Rightarrow \mathrm{(C)}</math>. | to be equal to <math>0</math>. We want <math>a+b</math>, which is the sum of the roots of the above quadratic. By [[Vieta’s formulas]], that is <math>\frac{280}{80} = \frac{7}{2} \Rightarrow \mathrm{(C)}</math>. | ||
Latest revision as of 15:23, 13 March 2023
Problem
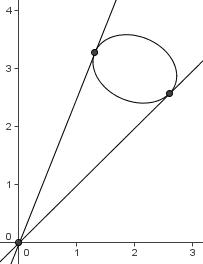
The graph of 
is an ellipse in the first quadrant of the 
-plane. Let 
and 
be the maximum and minimum values of 
over all points 
on the ellipse. What is the value of 
?
Solution
represents the slope of a line passing through the origin. It follows that since a line 
intersects the ellipse at either 
or 
points, the minimum and maximum are given when the line is a tangent, with only one point of intersection. Substituting,
![\[2x^2 + x(mx) + 3(mx)^2 - 11x - 20(mx) + 40 = 0\]](http://latex.artofproblemsolving.com/7/8/1/7810f02a1d842903268ef4e400f6355a7262fa0b.png)
Rearranging by the degree of 
,
![\[(3m^2 + m + 2)x^2 - (20m + 11)x + 40 = 0\]](http://latex.artofproblemsolving.com/3/d/b/3db7670b17d2532db53dee1c1c5e8c1cc7a786c5.png)
Since the line 
is tangent to the ellipse, we want the discriminant,
![\[(20m+11)^2 - 4\cdot 40 \cdot (3m^2 + m + 2) = -80m^2 + 280m - 199\]](http://latex.artofproblemsolving.com/1/0/b/10b41331a8f9d71b05e9dae9769abf4b648dce70.png)
to be equal to 
. We want , which is the sum of the roots of the above quadratic. By Vieta’s formulas, that is 
.
See also
| 2004 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 20 |
Followed by Problem 22 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
