Difference between revisions of "2007 AMC 12A Problems/Problem 19"

Latest revision as of 11:09, 3 November 2024

Problem

Triangles $ABC$ and $ADE$ have areas $2007$ and $7002,$ respectively, with $B = (0,0),$ $C = (223,0),$ $D = (680,380),$ and $E = (689,389).$ What is the sum of all possible x coordinates of $A$ ?

$\mathrm{(A)}\ 282 \qquad \mathrm{(B)}\ 300 \qquad \mathrm{(C)}\ 600 \qquad \mathrm{(D)}\ 900 \qquad \mathrm{(E)}\ 1200$

Solution

Solution 1

From $k = [ABC] = \frac 12bh$ , we have that the height of $\triangle ABC$ is $h = \frac{2k}{b} = \frac{2007 \cdot 2}{223} = 18$ . Thus $A$ lies on the lines $y = \pm 18 \quad \mathrm{(1)}$ .

$DE = 9\sqrt{2}$ using 45-45-90 triangles, so in $\triangle ADE$ we have that $h = \frac{2 \cdot 7002}{9\sqrt{2}} = 778\sqrt{2}$ . The slope of $DE$ is $1$ , so the equation of the line is $y = x + b \Longrightarrow b = (380) - (680) = -300 \Longrightarrow y = x - 300$ . The point $A$ lies on one of two parallel lines that are $778\sqrt{2}$ units away from $\overline{DE}$ . Now take an arbitrary point on the line $\overline{DE}$ and draw the perpendicular to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90 $\triangle$ , so the straight line down has a length of $778\sqrt{2} \cdot \sqrt{2} = 1556$ . Now we note that the y-intercept of the parallel lines is either $1556$ units above or below the y-intercept of line $\overline{DE}$ ; hence the equation of the parallel lines is $y = x - 300 \pm 1556 \Longrightarrow x = y + 300 \pm 1556 \quad \mathrm{(2)}$ .

We just need to find the intersections of these two lines and sum up the values of the x-coordinates. Substituting the $\mathrm{(1)}$ into $\mathrm{(2)}$ , we get $x = \pm 18 + 300 \pm 1556 = 4(300) = 1200 \Longrightarrow \mathrm{(E)}$ .

Solution 2

We are finding the intersection of two pairs of parallel lines, which will form a parallelogram. The centroid of this parallelogram is just the intersection of $\overline{BC}$ and $\overline{DE}$ , which can easily be calculated to be $(300,0)$ . Now the sum of the x-coordinates is just $4(300) = 1200$ .

Solution 3 (Bashing but very straightforward)

After we compute that the y-value can be either $y = \pm 18$ and realize there are four total values (each pair being equally spaced on their respective y-lines of $\pm 18$ ), we can use an easy application of the Shoelace Theorem to figure out the values of X. Since we already know the two distances (positive y and negative y) will be the same, then we can simply plug in y=18, compute the sum of the two corresponding x-values and multiply it by two to get our answer which is $2(600) = 1200 \Longrightarrow \mathrm{(E)}$

- Zephyrica

Solution 4 (intense bashing, similar to Solution 3)

We can use the shoelace theorem to first find that the y-coordinate of $A$ can be $-18$ or $18$ . Then we can apply shoelace again to find the $4$ possible x-coordinates, namely $-1274$ , $-1238$ , $1838$ , and $1874$ . Adding these up, we get $1200 \Longrightarrow \mathrm{(E)}$ .

~ erinb28lms

@@ Line 1: / Line 1: @@
 == Problem ==
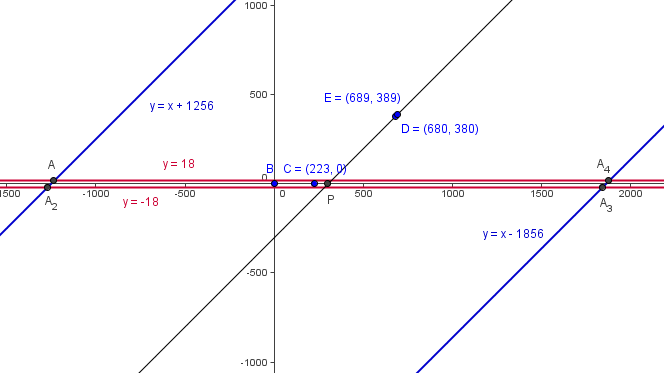
-[[Triangle]]s <math>ABC</math> and <math>ADE</math> have [[area]]s <math>2007</math> and <math>7002,</math> respectively, with <math>B = (0,0),</math> <math>C = (223,0),</math> <math>D = (680,380),</math> and <math>E = (689,389).</math> What is the sum of all possible x-coordinates of <math>A</math>?
+[[Triangle]]s <math>ABC</math> and <math>ADE</math> have [[area]]s <math>2007</math> and <math>7002,</math> respectively, with <math>B = (0,0),</math> <math>C = (223,0),</math> <math>D = (680,380),</math> and <math>E = (689,389).</math> What is the sum of all possible x coordinates of <math>A</math>?
 <math>\mathrm{(A)}\ 282 \qquad \mathrm{(B)}\ 300 \qquad \mathrm{(C)}\ 600 \qquad \mathrm{(D)}\ 900 \qquad \mathrm{(E)}\ 1200</math>
-__TOC__
+==Solution==
-== Solution ==
 [[Image:2007_12A_AMC-19.png]]
-=== Solution 1 ===
+==Solution 1==
 From <math>k = [ABC] = \frac 12bh</math>, we have that the height of <math>\triangle ABC</math> is <math>h = \frac{2k}{b} = \frac{2007 \cdot 2}{223} = 18</math>. Thus <math>A</math> lies on the lines <math>y = \pm 18 \quad \mathrm{(1)}</math>.
 <math>DE = 9\sqrt{2}</math> using 45-45-90 triangles, so in <math>\triangle ADE</math> we have that <math>h = \frac{2 \cdot 7002}{9\sqrt{2}} = 778\sqrt{2}</math>. The slope of <math>DE</math> is <math>1</math>, so the equation of the line is <math>y = x + b \Longrightarrow b = (380) - (680) = -300 \Longrightarrow y = x - 300</math>. The point <math>A</math> lies on one of two [[parallel]] lines that are <math>778\sqrt{2}</math> units away from <math>\overline{DE}</math>. Now take an arbitrary point on the line <math>\overline{DE}</math> and draw the [[perpendicular]] to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90 <math>\triangle</math>, so the straight line down has a length of <math>778\sqrt{2} \cdot \sqrt{2} = 1556</math>. Now we note that the [[y-intercept]] of the parallel lines is either <math>1556</math> units above or below the y-intercept of line <math>\overline{DE}</math>; hence the equation of the parallel lines is <math>y = x - 300 \pm 1556 \Longrightarrow x = y + 300 \pm 1556 \quad \mathrm{(2)}</math>.
-We just need to find the intersections of these two lines and sum up the values of the [[x-coordinates]]. Substituting the <math>\mathrm{(1)}</math> into <math>\mathrm{(2)}</math>, we get <math>x = \pm 18 + 300 \pm 1556 = 4(300) = 1200 \Longrightarrow \mathrm{(E)}</math>.
+We just need to find the intersections of these two lines and sum up the values of the x-coordinates. Substituting the <math>\mathrm{(1)}</math> into <math>\mathrm{(2)}</math>, we get <math>x = \pm 18 + 300 \pm 1556 = 4(300) = 1200 \Longrightarrow \mathrm{(E)}</math>.
-=== Solution 2 ===
+==Solution 2==
 We are finding the intersection of two pairs of [[parallel]] lines, which will form a [[parallelogram]]. The [[centroid]] of this parallelogram is just the intersection of <math>\overline{BC}</math> and <math>\overline{DE}</math>, which can easily be calculated to be <math>(300,0)</math>. Now the sum of the x-coordinates is just <math>4(300) = 1200</math>.
-== See also ==
+==Solution 3 (Bashing but very straightforward)==
+After we compute that the y-value can be either <math>y = \pm 18</math> and realize there are four total values (each pair being equally spaced on their respective y-lines of <math>\pm 18</math>), we can use an easy application of the [[Shoelace Theorem]] to figure out the values of X. Since we already know the two distances (positive y and negative y) will be the same, then we can simply plug in y=18, compute the sum of the two corresponding x-values and multiply it by two to get our answer which is <math>2(600) = 1200 \Longrightarrow \mathrm{(E)}</math>
+- Zephyrica
+==Solution 4 (intense bashing, similar to Solution 3)==
+We can use the shoelace theorem to first find that the y-coordinate of <math>A</math> can be <math>-18</math> or <math>18</math>. Then we can apply shoelace again to find the <math>4</math> possible x-coordinates, namely <math>-1274</math>, <math>-1238</math>, <math>1838</math>, and <math>1874</math>. Adding these up, we get <math>1200 \Longrightarrow \mathrm{(E)}</math>.
+~ erinb28lms
+== See Also ==
 {{AMC12 box|year=2007|ab=A|num-b=18|num-a=20}}
 [[Category:Introductory Geometry Problems]]
 {{MAA Notice}}

2007 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 18	Followed by Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search