Difference between revisions of "2005 AMC 12A Problems/Problem 7"

Revision as of 12:59, 23 September 2007

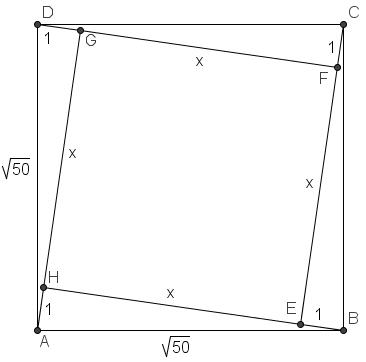
Problem

Square $EFGH$ is inside the square $ABCD$ so that each side of $EFGH$ can be extended to pass through a vertex of $ABCD$ . Square $ABCD$ has side length $\sqrt {50}$ and $BE = 1$ . What is the area of the inner square $EFGH$ ?

$(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42$

Solution

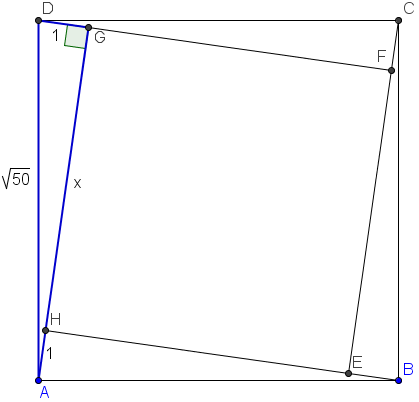
Arguable the hardest part of this question is to visualize the diagram. Since each side of $EFGH$ can be extended to pass through a vertex of $ABCD$ , we realize that $EFGH$ must be tilted in such a fashion. Let a side of $EFGH$ be $x$ .

Notice the right triangle (in blue) with legs $1, x+1$ and hypotenuse $\sqrt{50}$ . By the Pythagorean Theorem, we have $1^2 + (x+1)^2 = (\sqrt{50})^2 \Longrightarrow (x+1)^2 = 49 \Longrightarrow x = 6$ . Thus, $[EFGH] = x^2 = 36\ \mathrm{(C)}$

2005 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 6	Followed by Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

@@ Line 3: / Line 3: @@
 <math>
-(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 10 \qquad (\mathrm {E})\ 40
+(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42
 </math>
 == Solution ==

Page

Toolbox

Search

Difference between revisions of "2005 AMC 12A Problems/Problem 7"

Revision as of 12:59, 23 September 2007

Problem

Solution

See also