Difference between revisions of "2022 AIME I Problems/Problem 15"

Revision as of 11:09, 25 March 2023

Problem

Let $x,$ $y,$ and $z$ be positive real numbers satisfying the system of equations: $\begin{align*} \sqrt{2x-xy} + \sqrt{2y-xy} &= 1 \\ \sqrt{2y-yz} + \sqrt{2z-yz} &= \sqrt2 \\ \sqrt{2z-zx} + \sqrt{2x-zx} &= \sqrt3. \end{align*}$ Then $\left[ (1-x)(1-y)(1-z) \right]^2$ can be written as $\frac{m}{n},$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Solution 1 (geometric interpretation)

First, we note that we can let a triangle exist with side lengths $\sqrt{2x}$ , $\sqrt{2z}$ , and opposite altitude $\sqrt{xz}$ . This shows that the third side, which is the nasty square-rooted sum, is going to have the length equal to the sum on the right - let this be $l$ for symmetry purposes. So, we note that if the angle opposite the side with length $\sqrt{2x}$ has a value of $\theta$ , then the altitude has length $\sqrt{2z} \cdot \sin(\theta) = \sqrt{xz}$ and thus $\sin(\theta) = \sqrt{\frac{x}{2}}$ so $x=2\sin^2(\theta)$ and the triangle side with length $\sqrt{2x}$ is equal to $2\sin(\theta)$ .

We can symmetrically apply this to the two other triangles, and since by law of sines, we have $\frac{2\sin(\theta)}{\sin(\theta)} = 2R \to R=1$ is the circumradius of that triangle. Hence. we calculate that with $l=1, \sqrt{2}$ , and $\sqrt{3}$ , the angles from the third side with respect to the circumcenter are $120^{\circ}, 90^{\circ}$ , and $60^{\circ}$ . This means that by half angle arcs, we see that we have in some order, $x=2\sin^2(\alpha)$ , $x=2\sin^2(\beta)$ , and $z=2\sin^2(\gamma)$ (not necessarily this order, but here it does not matter due to symmetry), satisfying that $\alpha+\beta=180^{\circ}-\frac{120^{\circ}}{2}$ , $\beta+\gamma=180^{\circ}-\frac{90^{\circ}}{2}$ , and $\gamma+\alpha=180^{\circ}-\frac{60^{\circ}}{2}$ . Solving, we get $\alpha=\frac{135^{\circ}}{2}$ , $\beta=\frac{105^{\circ}}{2}$ , and $\gamma=\frac{165^{\circ}}{2}$ .

We notice that $[(1-x)(1-y)(1-z)]^2=[\sin(2\alpha)\sin(2\beta)\sin(2\gamma)]^2=[\sin(135^{\circ})\sin(105^{\circ})\sin(165^{\circ})]^2$ $=\left(\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{6}-\sqrt{2}}{4} \cdot \frac{\sqrt{6}+\sqrt{2}}{4}\right)^2 = \left(\frac{\sqrt{2}}{8}\right)^2=\frac{1}{32} \to \boxed{033}. \blacksquare$

- kevinmathz

Solution 2 (pure algebraic trig, easy to follow)

(This eventually whittles down to the same concept as Solution 1)

Note that in each equation in this system, it is possible to factor $\sqrt{x}$ , $\sqrt{y}$ , or $\sqrt{z}$ from each term (on the left sides), since each of $x$ , $y$ , and $z$ are positive real numbers. After factoring out accordingly from each terms one of $\sqrt{x}$ , $\sqrt{y}$ , or $\sqrt{z}$ , the system should look like this: $\begin{align*} \sqrt{x}\cdot\sqrt{2-y} + \sqrt{y}\cdot\sqrt{2-x} &= 1 \\ \sqrt{y}\cdot\sqrt{2-z} + \sqrt{z}\cdot\sqrt{2-y} &= \sqrt2 \\ \sqrt{z}\cdot\sqrt{2-x} + \sqrt{x}\cdot\sqrt{2-z} &= \sqrt3. \end{align*}$ This should give off tons of trigonometry vibes. To make the connection clear, $x = 2\cos^2 \alpha$ , $y = 2\cos^2 \beta$ , and $z = 2\cos^2 \theta$ is a helpful substitution: $\begin{align*} \sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \beta} + \sqrt{2\cos^2 \beta}\cdot\sqrt{2-2\cos^2 \alpha} &= 1 \\ \sqrt{2\cos^2 \beta}\cdot\sqrt{2-2\cos^2 \theta} + \sqrt{2\cos^2 \theta}\cdot\sqrt{2-2\cos^2 \beta} &= \sqrt2 \\ \sqrt{2\cos^2 \theta}\cdot\sqrt{2-2\cos^2 \alpha} + \sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \theta} &= \sqrt3. \end{align*}$ From each equation $\sqrt{2}^2$ can be factored out, and when every equation is divided by 2, we get: $\begin{align*} \sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \beta} + \sqrt{\cos^2 \beta}\cdot\sqrt{1-\cos^2 \alpha} &= \frac{1}{2} \\ \sqrt{\cos^2 \beta}\cdot\sqrt{1-\cos^2 \theta} + \sqrt{\cos^2 \theta}\cdot\sqrt{1-\cos^2 \beta} &= \frac{\sqrt2}{2} \\ \sqrt{\cos^2 \theta}\cdot\sqrt{1-\cos^2 \alpha} + \sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \theta} &= \frac{\sqrt3}{2}. \end{align*}$ which simplifies to (using the Pythagorean identity $\sin^2 \phi + \cos^2 \phi = 1 \; \forall \; \phi \in \mathbb{C}$ ): $\begin{align*} \cos \alpha\cdot\sin \beta + \cos \beta\cdot\sin \alpha &= \frac{1}{2} \\ \cos \beta\cdot\sin \theta + \cos \theta\cdot\sin \beta &= \frac{\sqrt2}{2} \\ \cos \theta\cdot\sin \alpha + \cos \alpha\cdot\sin \theta &= \frac{\sqrt3}{2}. \end{align*}$ which further simplifies to (using sine addition formula $\sin(a + b) = \sin a \cos b + \cos a \sin b$ ): $\begin{align*} \sin(\alpha + \beta) &= \frac{1}{2} \\ \sin(\beta + \theta) &= \frac{\sqrt2}{2} \\ \sin(\alpha + \theta) &= \frac{\sqrt3}{2}. \end{align*}$ Without loss of generality, taking the inverse sine of each equation yields a simple system: $\begin{align*} \alpha + \beta &= \frac{\pi}{6} \\ \beta + \theta &= \frac{\pi}{4} \\ \alpha + \theta &= \frac{\pi}{3}. \end{align*}$ giving solutions $\alpha = \frac{\pi}{8}$ , $\beta = \frac{\pi}{24}$ , $\theta = \frac{5\pi}{24}$ . Since these unknowns are directly related to our original unknowns, there are consequent solutions for those: $x = 2\cos^2\left(\frac{\pi}{8}\right)$ , $y = 2\cos^2\left(\frac{\pi}{24}\right)$ , and $z = 2\cos^2\left(\frac{5\pi}{24}\right)$ . When plugging into the expression $\left[ (1-x)(1-y)(1-z) \right]^2$ , noting that $-\cos 2\phi = 1 - 2\cos^2 \phi\; \forall \; \phi \in \mathbb{C}$ helps to simplify this expression into: $\left[ (-1)^3\left(\cos \left(2\cdot\frac{\pi}{8}\right)\cos \left(2\cdot\frac{\pi}{24}\right)\cos \left(2\cdot\frac{5\pi}{24}\right)\right)\right]^2 = \left[ (-1)\left(\cos \left(\frac{\pi}{4}\right)\cos \left(\frac{\pi}{12}\right)\cos \left(\frac{5\pi}{12}\right)\right)\right]^2$ Now, all the cosines in here are fairly standard: $\cos \frac{\pi}{4} = \frac{\sqrt{2}}{2}$ , $\;$ $\cos \frac{\pi}{12} = \frac{\sqrt{6} + \sqrt{2}}{4}$ , $\;$ and $\cos \frac{5\pi}{12} = \frac{\sqrt{6} - \sqrt{2}}{4}$ . With some final calculations: $(-1)^2\left(\frac{\sqrt{2}}{2}\right)^2\left(\frac{\sqrt{6} + \sqrt{2}}{4}\right)^2\left(\frac{\sqrt{6} - \sqrt{2}}{4}\right)^2 = \left(\frac{1}{2}\right)\left(\frac{2 + \sqrt{3}}{4}\right)\left(\frac{2 - \sqrt{3}}{4}\right) = \frac{\left(2 - \sqrt{3}\right)\left(2 + \sqrt{3}\right)}{2\cdot4\cdot4} = \frac{1}{32}.$ This is our answer in simplest form $\frac{m}{n}$ , so $m + n = 1 + 32 = \boxed{033}.$

~Oxymoronic15

solution 3

Let $1-x=a;1-y=b;1-z=c$ , rewrite those equations

$\sqrt{(1-a)(1+b)}+\sqrt{(1+a)(1-b)}=1$ ;

$\sqrt{(1-b)(1+c)}+\sqrt{(1+b)(1-c)}=\sqrt{2}$

$\sqrt{(1-a)(1+c)}+\sqrt{(1-c)(1+a)}=\sqrt{3}$

and solve for $m/n = (abc)^2 = a^2b^2c^2$

Square both sides and simplify, to get three equations:

$2ab-1=2\sqrt{(1-a^2)(1-b^2)}$

$2bc~ ~ ~ ~ ~ ~=2\sqrt{(1-b^2)(1-c^2)}$

$2ac+1=2\sqrt{(1-c^2)(1-a^2)}$

Square both sides again, and simplify to get three equations:

$a^2+b^2-ab=\frac{3}{4}$

$b^2+c^2~ ~ ~ ~ ~ ~=1$

$a^2+c^2+ac=\frac{3}{4}$

Subtract first and third equation, getting $(b+c)(b-c)=a(b+c)$ , $a=b-c$

Put it in first equation, getting $b^2-2bc+c^2+b^2-b(b-c)=b^2+c^2-bc=\frac{3}{4}$ , $bc=\frac{1}{4}$

Since $a^2=b^2+c^2-2bc=\frac{1}{2}$ , $m/n = a^2b^2c^2 = a^2(bc)^2 = \frac{1}{2}\left(\frac{1}{4}\right)^2=\frac{1}{32}$ and so the final answer is $\boxed{033}$

~bluesoul

Solution 4

Denote $u = 1 - x$ , $v = 1 - y$ , $w = 1 - z$ . Hence, the system of equations given in the problem can be written as $\begin{align*} \sqrt{(1-u)(1+v)} + \sqrt{(1+u)(1-v)} & = 1 \hspace{1cm} (1) \\ \sqrt{(1-v)(1+w)} + \sqrt{(1+v)(1-w)} & = \sqrt{2} \hspace{1cm} (2) \\ \sqrt{(1-w)(1+u)} + \sqrt{(1+w)(1-u)} & = \sqrt{3} . \hspace{1cm} (3) \end{align*}$

Each equation above takes the following form: $\sqrt{(1-a)(1+b)} + \sqrt{(1+a)(1-b)} = k .$

Now, we simplify this equation by removing radicals.

Denote $p = \sqrt{(1-a)(1+b)}$ and $q = \sqrt{(1+a)(1-b)}$ .

Hence, the equation above implies $\left\{ \begin{array}{l} p + q = k \\ p^2 = (1-a)(1+b) \\ q^2 = (1+a)(1-b) \end{array} \right..$

Hence, $q^2 - p^2 = (1+a)(1-b) - (1-a)(1+b) = 2 (a-b)$ . Hence, $q - p = \frac{q^2 - p^2}{p+q} = \frac{2}{k} (a-b)$ .

Because $p + q = k$ and $q - p = \frac{2}{k} (a-b)$ , we get $q = \frac{a-b}{k} + \frac{k}{2}$ . Plugging this into the equation $q^2 = (1+a)(1-b)$ and simplifying it, we get $a^2 + \left( k^2 - 2 \right) ab + b^2 = k^2 - \frac{k^4}{4} .$

Therefore, the system of equations above can be simplified as $\begin{align*} u^2 - uv + v^2 & = \frac{3}{4} \\ v^2 + w^2 & = 1 \\ w^2 + wu + u^2 & = \frac{3}{4} . \end{align*}$

Denote $w' = - w$ . The system of equations above can be equivalently written as $\begin{align*} u^2 - uv + v^2 & = \frac{3}{4} \hspace{1cm} (1') \\ v^2 + w'^2 & = 1 \hspace{1cm} (2') \\ w'^2 - w'u + u^2 & = \frac{3}{4} \hspace{1cm} (3') . \end{align*}$

Taking $(1') - (3')$ , we get $(v - w') (v + w' - u) = 0 .$

Thus, we have either $v - w' = 0$ or $v + w' - u = 0$ .

$\textbf{Case 1}$ : $v - w' = 0$ .

Equation (2') implies $v = w' = \pm \frac{1}{\sqrt{2}}$ .

Plugging $v$ and $w'$ into Equation (2), we get contradiction. Therefore, this case is infeasible.

$\textbf{Case 2}$ : $v + w' - u = 0$ .

Plugging this condition into (1') to substitute $u$ , we get $v^2 + v w' + w'^2 = \frac{3}{4} \hspace{1cm} (4) .$

Taking $(4) - (2')$ , we get $v w' = - \frac{1}{4} . \hspace{1cm} (5) .$

Taking (4) + (5), we get $\left( v + w' \right)^2 = \frac{1}{2} .$

Hence, $u^2 = \left( v + w' \right)^2 = \frac{1}{2}$ .

Therefore, $\begin{align*} \left[ (1-x)(1-y)(1-z) \right]^2 & = u^2 (vw)^2 \\ & = u^2 (vw')^2 \\ & = \frac{1}{2} \left( - \frac{1}{4} \right)^2 \\ & = \frac{1}{32} . \end{align*}$

Therefore, the answer is $1 + 32 = \boxed{\textbf{(033) }}$ . \end{solution}

~Steven Chen (www.professorchenedu.com)

Solution 5

Let $a=1-x$ , $b=1-y$ , and $c=1-z$ . Then, $\begin{align*} \sqrt{(1-a)(1+b)} + \sqrt{(1+a)(1-b)} &= 1 \hspace{15mm}(1) \\ \sqrt{(1-b)(1+c)} + \sqrt{(1+b)(1-c)} &= \sqrt2 \hspace{11.5mm}(2) \\ \sqrt{(1-a)(1+c)} + \sqrt{(1+a)(1-c)} &= \sqrt3. \hspace{10.5mm}(3). \end{align*}$

Notice that $\frac{1-a}{2}+\frac{1+a}{2}=1$ , $\frac{1-b}{2}+\frac{1+b}{2}=1$ , and $\frac{1-c}{2}+\frac{1+c}{2}=1$ . Let $\sin^2(\alpha)=(1-a)/2$ , $\sin^2(\beta)=(1-b)/2$ , and $\sin^2(\gamma)=(1-c)/2$ where $\alpha$ , $\beta$ , and $\gamma$ are real. Substituting into $(1)$ , $(2)$ , and $(3)$ yields $\begin{align*} \sin(\alpha + \beta) &= 1/2 \\ \sin(\alpha + \gamma) &= \sqrt2/2 \\ \sin(\beta + \gamma) &= \sqrt3/2. \end{align*}$ Thus, $\begin{align*} \alpha + \beta &= 30^{\circ} \\ \alpha + \gamma &= 45^{\circ} \\ \beta + \gamma &= 60^{\circ}, \end{align*}$ so $(\alpha, \beta, \gamma) = (15/2^{\circ}, 45/2^{\circ}, 75/2^{\circ})$ . Hence,

$abc = (1-2\sin^2(\alpha))(1-2\sin^2(\beta))(1-2\sin^2(\gamma))=\cos(15^{\circ})\cos(45^{\circ})\cos(75^{\circ})=\frac{\sqrt{2}}{8},$ so $(abc)^2=(\sqrt{2}/8)^2=\frac{1}{32}$ , for a final answer of $\boxed{033}$ .

Remark

The motivation for the trig substitution is that if $\sin^2(\alpha)=(1-a)/2$ , then $\cos^2(\alpha)=(1+a)/2$ , and when making the substitution in each equation of the initial set of equations, we obtain a new equation in the form of the sine addition formula.

~ Leo.Euler

Solution 6 (Geometric)

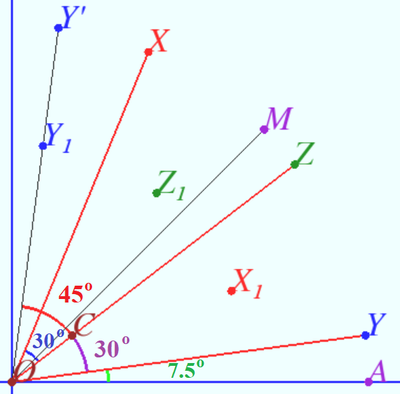
In given equations, $0 \leq x,y,z \leq 2,$ so we define some points: $\bar {O} = (0, 0), \bar {A} = (1, 0), \bar{M} = \left(\frac {1}{\sqrt{2}},\frac {1}{\sqrt{2}}\right),$ $\bar {X} = \left(\sqrt {\frac {x}{2}}, \sqrt{1 – \frac{x}{2}}\right), \bar {Y'} = \left(\sqrt {\frac {y}{2}}, \sqrt{1 – \frac{y}{2}}\right),$ $\bar {Y} = \left(\sqrt {1 – \frac{y}{2}},\sqrt{\frac {y}{2}}\right), \bar {Z} = \left(\sqrt {1 – \frac{z}{2}},\sqrt{\frac {z}{2}}\right).$ Notice, that $\mid \vec {AO} \mid = \mid \vec {MO} \mid = \mid \vec {XO} \mid =\mid \vec {YO} \mid = \mid \vec {Y'O} \mid =\mid \vec {ZO} \mid = 1$ and each points lies in the first quadrant.

We use given equations and get some scalar products: $(\vec {XO} \cdot \vec {YO}) = \frac {1}{2} = \cos \angle XOY \implies \angle XOY = 60 ^\circ,$ $(\vec {XO} \cdot \vec {ZO}) = \frac {\sqrt{3}}{2} = \cos \angle XOZ \implies \angle XOZ = 30^\circ,$ $(\vec {Y'O} \cdot \vec {ZO}) = \frac {1}{\sqrt{2}} = \cos \angle Y'OZ \implies \angle Y'OZ = 45^\circ.$ So $\angle YOZ = \angle XOY – \angle XOZ = 60 ^\circ – 30 ^\circ = 30 ^\circ, \angle Y'OY = \angle Y'OZ + \angle YOZ = 45^\circ + 30 ^\circ = 75^\circ.$

Points $Y$ and $Y'$ are simmetric with respect to $OM.$

Case 1 $\angle YOA = \frac{90^\circ – 75^\circ}{2} = 7.5^\circ, \angle ZOA = 30^\circ + 7.5^\circ = 37.5^\circ, \angle XOA = 60^\circ + 7.5^\circ = 67.5^\circ .$ $1 – x = \left(\sqrt{1 – \frac{x}{2}} \right)^2– \left(\sqrt{\frac {x}{2}}\right)^2 = \sin^2 \angle XOA – \cos^2 \angle XOA = –\cos 2 \angle XOA = –\cos 135^\circ,$ $1 – y = \cos 15^\circ, 1 – z = \cos 75^\circ \implies \left[ (1–x)(1–y)(1–z) \right]^2 = \left[ \sin 45^\circ \cdot \cos 15^\circ \cdot \sin 15^\circ \right]^2 =$ $=\left[ \frac {\sin 45^\circ \cdot \sin 30^\circ}{2} \right]^2 = \frac {1}{32} \implies \boxed{\textbf{033}}.$ Case 2

$\angle Y_1 OA = \frac{90^\circ + 75^\circ}{2} = 82.5^\circ, \angle Z_1 OA = 82.5^\circ – 30^\circ = 52.5^\circ, \angle X_1 OA = 82.5^\circ – 60^\circ = 22.5^\circ \implies \boxed{\textbf{033}}.$

vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/i6kDMbav2sk

~Math Gold Medalist

Video Solution

https://www.youtube.com/watch?v=ihKUZ5itcdA

~Steven Chen (www.professorchenedu.com)

@@ Line 10: / Line 10: @@
 ==Solution 1 (geometric interpretation)==
-First, we note that we can let a triangle exist with side lengths <math>\sqrt{2x}</math>, <math>\sqrt{2z}</math>, and opposite altitude <math>\sqrt{xz}</math>. This shows that the third side, which is the nasty square-rooted sum, is going to have the length equal to the sum on the right - let this be <math>l</math> for symmetry purposes. So, we note that if the angle opposite the side with length <math>\sqrt{2x}</math> has a value of <math>\sin(\theta)</math>, then the altitude has length <math>\sqrt{2z} \cdot \sin(\theta) = \sqrt{xz}</math> and thus <math>\sin(\theta) = \sqrt{\frac{x}{2}}</math> so <math>x=2\sin^2(\theta)</math> and the triangle side with length <math>\sqrt{2x}</math> is equal to <math>2\sin(\theta)</math>.
+First, we note that we can let a triangle exist with side lengths <math>\sqrt{2x}</math>, <math>\sqrt{2z}</math>, and opposite altitude <math>\sqrt{xz}</math>. This shows that the third side, which is the nasty square-rooted sum, is going to have the length equal to the sum on the right - let this be <math>l</math> for symmetry purposes. So, we note that if the angle opposite the side with length <math>\sqrt{2x}</math> has a value of <math>\theta</math>, then the altitude has length <math>\sqrt{2z} \cdot \sin(\theta) = \sqrt{xz}</math> and thus <math>\sin(\theta) = \sqrt{\frac{x}{2}}</math> so <math>x=2\sin^2(\theta)</math> and the triangle side with length <math>\sqrt{2x}</math> is equal to <math>2\sin(\theta)</math>.
 We can symmetrically apply this to the two other triangles, and since by law of sines, we have <math>\frac{2\sin(\theta)}{\sin(\theta)} = 2R \to R=1</math> is the circumradius of that triangle. Hence. we calculate that with <math>l=1, \sqrt{2}</math>, and <math>\sqrt{3}</math>, the angles from the third side with respect to the circumcenter are <math>120^{\circ}, 90^{\circ}</math>, and <math>60^{\circ}</math>. This means that by half angle arcs, we see that we have in some order, <math>x=2\sin^2(\alpha)</math>, <math>x=2\sin^2(\beta)</math>, and <math>z=2\sin^2(\gamma)</math> (not necessarily this order, but here it does not matter due to symmetry), satisfying that <math>\alpha+\beta=180^{\circ}-\frac{120^{\circ}}{2}</math>, <math>\beta+\gamma=180^{\circ}-\frac{90^{\circ}}{2}</math>, and <math>\gamma+\alpha=180^{\circ}-\frac{60^{\circ}}{2}</math>. Solving, we get <math>\alpha=\frac{135^{\circ}}{2}</math>, <math>\beta=\frac{105^{\circ}}{2}</math>, and <math>\gamma=\frac{165^{\circ}}{2}</math>.

2022 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "2022 AIME I Problems/Problem 15"

Revision as of 11:09, 25 March 2023

Contents

Problem

Solution 1 (geometric interpretation)

Solution 2 (pure algebraic trig, easy to follow)

solution 3

Solution 4

Solution 5

Solution 6 (Geometric)

Video Solution

Video Solution

See Also