Difference between revisions of "2004 AMC 12A Problems/Problem 22"
(+ spacing, imgs. Somebody should do a readibility check) |
|||
| Line 2: | Line 2: | ||
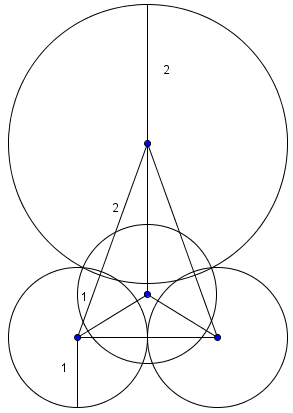
Three mutually [[tangent]] [[sphere]]s of [[radius]] <math>1</math> rest on a horizontal [[plane]]. A sphere of radius <math>2</math> rests on them. What is the [[distance]] from the plane to the top of the larger sphere? | Three mutually [[tangent]] [[sphere]]s of [[radius]] <math>1</math> rest on a horizontal [[plane]]. A sphere of radius <math>2</math> rests on them. What is the [[distance]] from the plane to the top of the larger sphere? | ||
| − | <math>\text {(A)} 3 + \frac {\sqrt {30}}{2} \qquad \text {(B)} 3 + \frac {\sqrt {69}}{3} \qquad \text {(C)} 3 + \frac {\sqrt {123}}{4}\qquad \text {(D)} \frac {52}{9}\qquad \text {(E)}3 + 2\sqrt2</math> | + | <math>\text {(A)}\ 3 + \frac {\sqrt {30}}{2} \qquad \text {(B)}\ 3 + \frac {\sqrt {69}}{3} \qquad \text {(C)}\ 3 + \frac {\sqrt {123}}{4}\qquad \text {(D)}\ \frac {52}{9}\qquad \text {(E)}\ 3 + 2\sqrt2</math> |
== Solution == | == Solution == | ||
| + | [[Image:2004_AMC12A-22a.png]] | ||
| + | |||
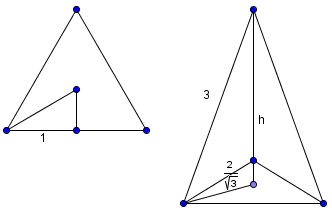
The height from the center of the bottom sphere to the plane is <math>1</math>, and from the center of the top sphere to the tip is <math>2</math>. We now need the vertical height of the centers. If we connect the centers, we get a triangular [[pyramid]] with an [[equilateral triangle]] base. The distance from the vertex of the equilateral triangle to its [[centroid]] can be found by <math>30-60-90 \triangle</math>s to be <math>\frac{2}{\sqrt{3}}</math>. | The height from the center of the bottom sphere to the plane is <math>1</math>, and from the center of the top sphere to the tip is <math>2</math>. We now need the vertical height of the centers. If we connect the centers, we get a triangular [[pyramid]] with an [[equilateral triangle]] base. The distance from the vertex of the equilateral triangle to its [[centroid]] can be found by <math>30-60-90 \triangle</math>s to be <math>\frac{2}{\sqrt{3}}</math>. | ||
| − | + | [[Image:2004_AMC12A-22b.png]] | |
By the [[Pythagorean Theorem]], we have <math>\left(\frac{2}{\sqrt{3}}\right)^2 + h^2 = 3^2 \Longrightarrow h = \frac{\sqrt{69}}{3}</math>. Adding the heights up, we get <math>\frac{\sqrt{69}}{3} + 1 + 2 = \frac{\sqrt{69} + 9}{3} \Rightarrow \mathrm{(B)}</math>. | By the [[Pythagorean Theorem]], we have <math>\left(\frac{2}{\sqrt{3}}\right)^2 + h^2 = 3^2 \Longrightarrow h = \frac{\sqrt{69}}{3}</math>. Adding the heights up, we get <math>\frac{\sqrt{69}}{3} + 1 + 2 = \frac{\sqrt{69} + 9}{3} \Rightarrow \mathrm{(B)}</math>. | ||
Revision as of 16:20, 4 December 2007
Problem
Three mutually tangent spheres of radius 
rest on a horizontal plane. A sphere of radius 
rests on them. What is the distance from the plane to the top of the larger sphere?
Solution
The height from the center of the bottom sphere to the plane is , and from the center of the top sphere to the tip is . We now need the vertical height of the centers. If we connect the centers, we get a triangular pyramid with an equilateral triangle base. The distance from the vertex of the equilateral triangle to its centroid can be found by 
s to be 
.
By the Pythagorean Theorem, we have 
. Adding the heights up, we get 
.
See also
| 2004 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 21 |
Followed by Problem 23 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
