Difference between revisions of "1998 AHSME Problems/Problem 16"
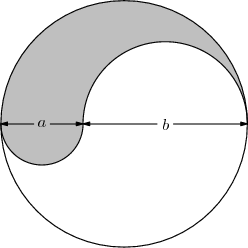
(Created page with "== Problem 16 == The figure shown is the union of a circle and two semicircles of diameters <math>a</math> and <math>b</math>, all of whose centers are collinear. The ratio of th...") |
Talkinaway (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | == Problem | + | == Problem == |
The figure shown is the union of a circle and two semicircles of diameters <math>a</math> and <math>b</math>, all of whose centers are collinear. The ratio of the area, of the shaded region to that of the unshaded region is | The figure shown is the union of a circle and two semicircles of diameters <math>a</math> and <math>b</math>, all of whose centers are collinear. The ratio of the area, of the shaded region to that of the unshaded region is | ||
| Line 6: | Line 6: | ||
<math> \mathrm{(A) \ } \sqrt{\frac ab} \qquad \mathrm{(B) \ }\frac ab \qquad \mathrm{(C) \ } \frac{a^2}{b^2} \qquad \mathrm{(D) \ }\frac{a+b}{2b} \qquad \mathrm{(E) \ } \frac{a^2 + 2ab}{b^2 + 2ab}</math> | <math> \mathrm{(A) \ } \sqrt{\frac ab} \qquad \mathrm{(B) \ }\frac ab \qquad \mathrm{(C) \ } \frac{a^2}{b^2} \qquad \mathrm{(D) \ }\frac{a+b}{2b} \qquad \mathrm{(E) \ } \frac{a^2 + 2ab}{b^2 + 2ab}</math> | ||
| − | + | ==Solution== | |
| + | |||
| + | To simplify calculations, double the radius of the large circle from <math>\frac{a + b}{2}</math> to <math>a + b</math>. Each region is similar to the old region, so this should not change the ratio of any areas. | ||
| + | |||
| + | In other words, relabel <math>a</math> and <math>b</math> to <math>2a</math> and <math>2b</math>. | ||
| + | |||
| + | |||
| + | The area of the whole circle is <math>A_{big} = \pi\cdot (a + b)^2</math> | ||
| + | |||
| + | The area of the white area is about <math>\frac{A_{big}}{2}</math>, which is the bottom half of the circle. However, you need to subtract the little shaded semicircle on the bottom, and add the area of the big unshaded semicircle on top. Thus, it is actually <math>A_{white} = \frac{1}{2}\pi\cdot (a+b)^2 - \frac{1}{2}\pi a^2 + \frac{1}{2}\pi b^2</math> | ||
| + | |||
| + | Factoring gives <math>A_{white} = \frac{\pi}{2}\cdot (a^2 + 2ab + b^2 - a^2 + b^2)</math> | ||
| + | |||
| + | Simplfying the inside gives <math>A_{white} = \frac{\pi}{2}\cdot (2ab + b^2)</math> | ||
| + | |||
| + | <math>A_{white} = \pi(ab + b^2)</math> | ||
| + | |||
| + | With similar calculations, or noting the symmetry of the situation, <math>A_{grey} = \pi(ab + a^2)</math> | ||
| + | |||
| + | The desired ratio is thus <math>\frac{ab + a^2}{ab + b^2} = \frac{a(a+b)}{b(a+b)}</math>, which is option <math>\boxed{B}</math>. | ||
| + | |||
| + | == See also == | ||
| + | {{AHSME box|year=1998|num-b=15|num-a=17}} | ||
Revision as of 00:16, 8 August 2011
Problem
The figure shown is the union of a circle and two semicircles of diameters ![]() and
and ![]() , all of whose centers are collinear. The ratio of the area, of the shaded region to that of the unshaded region is
, all of whose centers are collinear. The ratio of the area, of the shaded region to that of the unshaded region is
![]()
Solution
To simplify calculations, double the radius of the large circle from ![]() to
to ![]() . Each region is similar to the old region, so this should not change the ratio of any areas.
. Each region is similar to the old region, so this should not change the ratio of any areas.
In other words, relabel ![]() and
and ![]() to
to ![]() and
and ![]() .
.
The area of the whole circle is ![]()
The area of the white area is about ![]() , which is the bottom half of the circle. However, you need to subtract the little shaded semicircle on the bottom, and add the area of the big unshaded semicircle on top. Thus, it is actually
, which is the bottom half of the circle. However, you need to subtract the little shaded semicircle on the bottom, and add the area of the big unshaded semicircle on top. Thus, it is actually ![]()
Factoring gives ![]()
Simplfying the inside gives ![]()
![]()
With similar calculations, or noting the symmetry of the situation, ![]()
The desired ratio is thus ![]() , which is option
, which is option ![]() .
.
See also
| 1998 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 15 |
Followed by Problem 17 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||