1998 AHSME Problems
| 1998 AHSME (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 Problem 26
- 27 Problem 27
- 28 Problem 28
- 29 Problem 29
- 30 Problem 30
- 31 See also
Problem 1
Each of the sides of five congruent rectangles is labeled with an integer. In rectangle A, ![]() . In rectangle B,
. In rectangle B, ![]() . In rectangle C,
. In rectangle C, ![]() . In rectangle D,
. In rectangle D, ![]() . In rectangle E,
. In rectangle E, ![]() . These five rectangles are placed, without rotating or reflecting, in position as below. Which of the rectangle is the top leftmost one?
. These five rectangles are placed, without rotating or reflecting, in position as below. Which of the rectangle is the top leftmost one?
![[asy] draw((0,5)--(0,7)--(3,7)--(3,5)--cycle); draw((0,4)--(9,4)--(9,2)--(6,2)--(6,0)--(0,0)--cycle); draw((3,0)--(3,4));draw((6,2)--(6,4));draw((0,2)--(6,2)); label("$w$",(0,6),(-1,0));label("$x$",(1.5,7),(0,1));label("$y$",(3,6),(1,0));label("$z$",(1.5,5),(0,-1)); [/asy]](http://latex.artofproblemsolving.com/f/d/4/fd4ce8e9f69eccb7bc297cde34a60f44244789af.png)
![]()
Problem 2
Letters ![]() and
and ![]() represent four different digits selected from
represent four different digits selected from ![]() If
If ![]() is an integer that is as large as possible, what is the value of
is an integer that is as large as possible, what is the value of ![]() ?
?
![]()
Problem 3
If ![]() and
and ![]() are digits for which
are digits for which
![\[\begin{array}{rccc}&\ \texttt{7}& \texttt{a}&\texttt{2}\\ -&\ \texttt{4}&\texttt{8}&\texttt{b} \\ \hline &\ \texttt{c}&\texttt{7}& \texttt{3} \end{array}\]](http://latex.artofproblemsolving.com/5/d/d/5dd159f67012d65c4f8c93704e20e8fd10ed779a.png)
then ![]()
![]()
Problem 4
Define ![]() to mean
to mean ![]() , where
, where ![]() . What is the value of
. What is the value of
![]()
Problem 5
If ![]() what is the value of
what is the value of ![]() ?
?
![]()
Problem 6
If ![]() is written as a product of two positive integers whose difference is as small as possible, then the difference is
is written as a product of two positive integers whose difference is as small as possible, then the difference is
![]()
Problem 7
If ![]() , then
, then ![]()
![]()
Problem 8
A square with sides of length ![]() is divided into two congruent trapezoids and a pentagon, which have equal areas, by joining the center of the square with points on three of the sides, as shown. Find
is divided into two congruent trapezoids and a pentagon, which have equal areas, by joining the center of the square with points on three of the sides, as shown. Find ![]() , the length of the longer parallel side of each trapezoid.
, the length of the longer parallel side of each trapezoid.
![[asy]size(150); pointpen = black; pathpen = black+linewidth(0.7); D(unitsquare); D((0,0)); D((1,0)); D((1,1)); D((0,1)); D(D((.5,.5))--D((1,.5))); D(D((.17,1))--(.5,.5)--D((.17,0))); MP("x",(.58,1),N); [/asy]](http://latex.artofproblemsolving.com/c/d/3/cd377f61d1a4292ea7abca47018c6113286b61ae.png)
![]()
Problem 9
A speaker talked for sixty minutes to a full auditorium. Twenty percent of the audience heard the entire talk and ten percent slept through the entire talk. Half of the remainder heard one third of the talk and the other half heard two thirds of the talk. What was the average number of minutes of the talk heard by members of the audience?
![]()
Problem 10
A large square is divided into a small square surrounded by four congruent rectangles as shown. The perimeter of each of the congruent rectangles is ![]() . What is the area of the large square?
. What is the area of the large square?
![[asy]pathpen = black+linewidth(0.7); D((0,0)--(7,0)--(7,7)--(0,7)--cycle); D((1,0)--(1,6)); D((0,6)--(6,6)); D((1,1)--(7,1)); D((6,7)--(6,1)); [/asy]](http://latex.artofproblemsolving.com/3/5/1/351dd6615f83399259278b9bb833588e02536bc0.png)
![]()
Problem 11
Let ![]() be a rectangle. How many circles in the plane of
be a rectangle. How many circles in the plane of ![]() have a diameter both of whose endpoints are vertices of
have a diameter both of whose endpoints are vertices of ![]() ?
?
![]()
Problem 12
How many different prime numbers are factors of ![]() if
if
![]()
Problem 13
Walter rolls four standard six-sided dice and finds that the product of the numbers of the upper faces is ![]() . Which of he following could not be the sum of the upper four faces?
. Which of he following could not be the sum of the upper four faces?
![]()
Problem 14
A parabola has vertex of ![]() and has two
and has two ![]() intercepts, one positive, and one negative. If this parabola is the graph of
intercepts, one positive, and one negative. If this parabola is the graph of ![]() which of
which of ![]() and
and ![]() must be positive?
must be positive?
![]()
Problem 15
A regular hexagon and an equilateral triangle have equal areas. What is the ratio of the length of a side of the triangle to the length of a side of the hexagon?
![]()
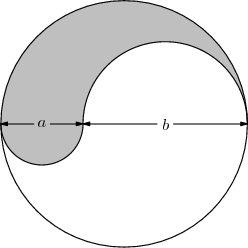
Problem 16
The figure shown is the union of a circle and two semicircles of diameters ![]() and
and ![]() , all of whose centers are collinear. The ratio of the area, of the shaded region to that of the unshaded region is
, all of whose centers are collinear. The ratio of the area, of the shaded region to that of the unshaded region is
![]()
Problem 17
Let ![]() be a function with the two properties:
be a function with the two properties:
- (a) for any two real numbers
 and
and  ,
,  , and
, and - (b)

What is the value of ![]()
![]()
Problem 18
A right circular cone of volume ![]() , a right circular cylinder of volume
, a right circular cylinder of volume ![]() , and a sphere of volume
, and a sphere of volume ![]() all have the same radius, and the common height of the cone and the cylinder is equal to the diameter of the sphere. Then
all have the same radius, and the common height of the cone and the cylinder is equal to the diameter of the sphere. Then
![]()
Problem 19
How many triangles have area ![]() and vertices at
and vertices at ![]() and
and ![]() for some angle
for some angle ![]() ?
?
![]()
Problem 20
Three cards, each with a positive integer written on it, are lying face-down on a table. Casey, Stacy, and Tracy are told that
- (a) the numbers are all different,
- (b) they sum to
 , and
, and - (c) they are in increasing order, left to right.
First, Casey looks at the number on the leftmost card and says, "I don't have enough information to determine the other two numbers." Then Tracy looks at the number on the rightmost card and says, "I don't have enough information to determine the other two numbers." Finally, Stacy looks at the number on the middle card and says, "I don't have enough information to determine the other two numbers." Assume that each person knows that the other two reason perfectly and hears their comments. What number is on the middle card?
![]()
Problem 21
In an ![]() -meter race, Sunny is exactly
-meter race, Sunny is exactly ![]() meters ahead of Windy when Sunny finishes the race. The next time they race, Sunny sportingly starts
meters ahead of Windy when Sunny finishes the race. The next time they race, Sunny sportingly starts ![]() meters behind Windy, who is at the starting line. Both runners run at the same constant speed as they did in the first race. How many meters ahead is Sunny when Sunny finishes the second race?
meters behind Windy, who is at the starting line. Both runners run at the same constant speed as they did in the first race. How many meters ahead is Sunny when Sunny finishes the second race?
![]()
Problem 22
What is the value of the expression
![]()
Problem 23
The graphs of ![]() and
and ![]() intersect when
intersect when ![]() satisfies
satisfies ![]() , and for no other values of
, and for no other values of ![]() . Find
. Find ![]() .
.
![]()
Problem 24
Call a ![]() -digit telephone number
-digit telephone number ![]() memorable if the prefix sequence
memorable if the prefix sequence ![]() is exactly the same as either of the sequences
is exactly the same as either of the sequences ![]() or
or ![]() (possibly both). Assuming that each
(possibly both). Assuming that each ![]() can be any of the ten decimal digits
can be any of the ten decimal digits ![]() , the number of different memorable telephone numbers is
, the number of different memorable telephone numbers is
![]()
Problem 25
A piece of graph paper is folded once so that ![]() is matched with
is matched with ![]() , and
, and ![]() is matched with
is matched with ![]() . Find
. Find ![]() .
.
![]()
Problem 26
In quadrilateral ![]() , it is given that
, it is given that ![]() , angles
, angles ![]() and
and ![]() are right angles,
are right angles, ![]() , and
, and ![]() . Then
. Then ![]()
![]()
Problem 27
A ![]() cube is composed of twenty-seven
cube is composed of twenty-seven ![]() cubes. The big cube is ‘tunneled’ as follows: First the six
cubes. The big cube is ‘tunneled’ as follows: First the six ![]() cubes which make up the center of each face as well as the center
cubes which make up the center of each face as well as the center ![]() cube are removed as shown. Second, each of the twenty remaining
cube are removed as shown. Second, each of the twenty remaining ![]() cubes is diminished in the same way. That is, the center facial unit cubes as well as each center cube are removed. The surface area of the final figure is
cubes is diminished in the same way. That is, the center facial unit cubes as well as each center cube are removed. The surface area of the final figure is
![]()
Problem 28
In triangle ![]() , angle
, angle ![]() is a right angle and
is a right angle and ![]() . Point
. Point ![]() is located on
is located on ![]() so that angle
so that angle ![]() is twice angle
is twice angle ![]() . If
. If ![]() , then
, then ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
![]()
Problem 29
A point ![]() in the plane is called a lattice point if both
in the plane is called a lattice point if both ![]() and
and ![]() are integers. The area of the largest square that contains exactly three lattice points in its interior is closest to
are integers. The area of the largest square that contains exactly three lattice points in its interior is closest to
![]()
Problem 30
For each positive integer ![]() , let
, let
Let ![]() denote the smallest positive integer for which the rightmost nonzero digit of
denote the smallest positive integer for which the rightmost nonzero digit of ![]() is odd. The rightmost nonzero digit of
is odd. The rightmost nonzero digit of ![]() is
is
![]()
See also
| 1998 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by 1997 AHSME |
Followed by 1999 AHSME | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()