Difference between revisions of "2001 AMC 10 Problems/Problem 5"
Anthonyjang (talk | contribs) (→Solution) |
|||
| Line 15: | Line 15: | ||
{{AMC10 box|year=2001|num-b=4|num-a=6}} | {{AMC10 box|year=2001|num-b=4|num-a=6}} | ||
| + | {{MAA Notice}} | ||
Revision as of 10:10, 4 July 2013
Problem
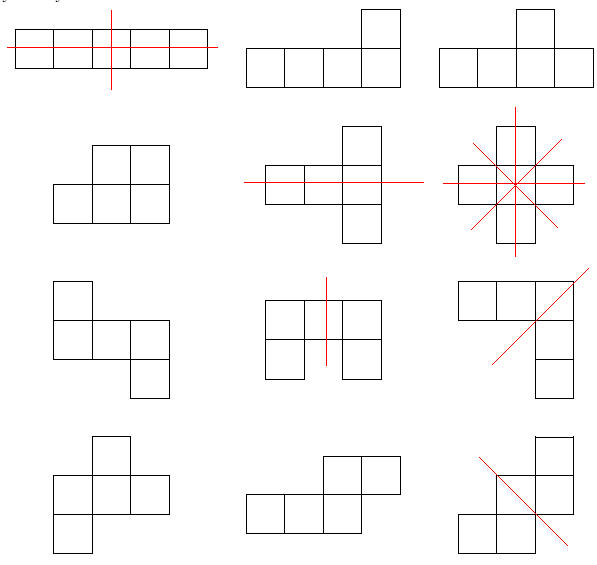
How many of the twelve pentominoes pictured below at least one line of symmetry?
![]()
Solution
The ones with lines over the shapes have at least one line of symmetry. Counting the number of shapes that have line(s) on them,
we find ![]() pentominoes.
pentominoes.
See Also
| 2001 AMC 10 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()