Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2001 AMC 10 Problems/Problem 21"
Line 5: Line 5:
 
<math> \textbf{(A)}\ \frac{8}3\qquad\textbf{(B)}\ \frac{30}{11}\qquad\textbf{(C)}\ 3\qquad\textbf{(D)}\ \frac{25}{8}\qquad\textbf{(E)}\ \frac{7}{2} </math>
 
<math> \textbf{(A)}\ \frac{8}3\qquad\textbf{(B)}\ \frac{30}{11}\qquad\textbf{(C)}\ 3\qquad\textbf{(D)}\ \frac{25}{8}\qquad\textbf{(E)}\ \frac{7}{2} </math>
  
−
==Solution==
+
==Solution 1==
  
 
<asy>
 
<asy>
Line 35: Line 35:
  
 
Let the diameter of the cylinder be <math> 2r </math>. Examining the cross section of the cone and cylinder, we find two similar triangles. Hence, <math> \frac{12-2r}{12}=\frac{2r}{10} </math> which we solve to find <math> r=\frac{30}{11} </math>. Our answer is <math> \boxed{\textbf{(B)}\ \frac{30}{11}} </math>.
 
Let the diameter of the cylinder be <math> 2r </math>. Examining the cross section of the cone and cylinder, we find two similar triangles. Hence, <math> \frac{12-2r}{12}=\frac{2r}{10} </math> which we solve to find <math> r=\frac{30}{11} </math>. Our answer is <math> \boxed{\textbf{(B)}\ \frac{30}{11}} </math>.
 +
 +
==Solution 2==
 +
 +
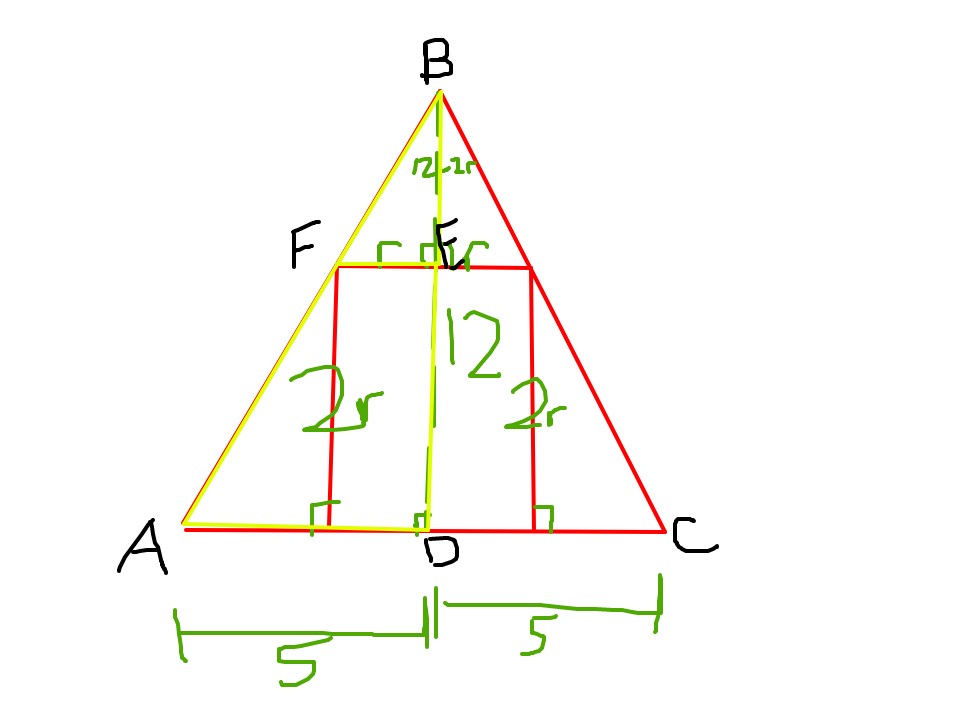
<math>\text{We can begin by drawing a diagram with the given information}</math>:
 +
 +
[[File:2001amc10solution.jpg]]
 +
 +
We are asked to find the radius of the cylinder, or <math>r</math> so we can look for similarity. We know that <math>\angle BEF = \angle BDA</math> and <math>\angle FBE = \angle ABD</math>, thus we have similarity between <math>\triangle BFE</math> and <math>\triangle BAD</math> by <math>AA</math> similarity.
 +
 +
Therefore, we can create an equation to find the length of the desired side. We know that:
 +
 +
<math>\frac{BE}{BD}=\frac{FE}{AD}.</math>
 +
 +
Plugging in yields:
 +
 +
<math>\frac{12-2r}{12}=\frac{r}{5}.</math>
 +
 +
Cross multiplying and simplifying gives:
 +
 +
<math>5(12-2r)=12r</math>
 +
 +
<math>\Downarrow</math>
 +
 +
<math> r=\frac{30}{11}.</math>
 +
 +
<math>Since the problem asks us to find the radius of the cylinder, we are done and the radius of the cylinder is</math>  <math>\boxed{\textbf{(B)}\ \frac{30}{11}}</math>.
 +
 +
~etvat
  
 
==See Also==
 
==See Also==

Revision as of 16:07, 15 February 2021

Problem

A right circular cylinder with its diameter equal to its height is inscribed in a right circular cone. The cone has diameter $10$ and altitude $12$, and the axes of the cylinder and cone coincide. Find the radius of the cylinder.

$\textbf{(A)}\ \frac{8}3\qquad\textbf{(B)}\ \frac{30}{11}\qquad\textbf{(C)}\ 3\qquad\textbf{(D)}\ \frac{25}{8}\qquad\textbf{(E)}\ \frac{7}{2}$

Solution 1

[asy] draw((5,0)--(-5,0)--(0,12)--cycle); unitsize(.75cm); draw((-30/11,0)--(-30/11,60/11)); draw((-30/11,60/11)--(30/11,60/11)); draw((30/11,60/11)--(30/11,0)); draw((0,0)--(0,12)); label("$2r$",(0,30/11),E); label("$12-2r$",(0,80/11),E); label("$2r$",(0,60/11),S); label("$10$",(0,0),S); label("$A$",(0,12),N); label("$B$",(-5,0),SW); label("$C$",(5,0),SE); label("$D$",(-30/11,60/11),W); label("$E$",(30/11,60/11),E); [/asy]




Let the diameter of the cylinder be $2r$. Examining the cross section of the cone and cylinder, we find two similar triangles. Hence, $\frac{12-2r}{12}=\frac{2r}{10}$ which we solve to find $r=\frac{30}{11}$. Our answer is $\boxed{\textbf{(B)}\ \frac{30}{11}}$.

Solution 2

$\text{We can begin by drawing a diagram with the given information}$:

2001amc10solution.jpg

We are asked to find the radius of the cylinder, or $r$ so we can look for similarity. We know that $\angle BEF = \angle BDA$ and $\angle FBE = \angle ABD$, thus we have similarity between $\triangle BFE$ and $\triangle BAD$ by $AA$ similarity.

Therefore, we can create an equation to find the length of the desired side. We know that:

$\frac{BE}{BD}=\frac{FE}{AD}.$

Plugging in yields:

$\frac{12-2r}{12}=\frac{r}{5}.$

Cross multiplying and simplifying gives:

$5(12-2r)=12r$

$\Downarrow$

$r=\frac{30}{11}.$

$Since the problem asks us to find the radius of the cylinder, we are done and the radius of the cylinder is$ $\boxed{\textbf{(B)}\ \frac{30}{11}}$.

~etvat

See Also

2001 AMC 10 (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2001_AMC_10_Problems/Problem_21&oldid=146961"