Difference between revisions of "2010 AMC 10A Problems/Problem 14"

Revision as of 13:38, 13 August 2017

Problem

Triangle $ABC$ has $AB=2 \cdot AC$ . Let $D$ and $E$ be on $\overline{AB}$ and $\overline{BC}$ , respectively, such that $\angle BAE = \angle ACD$ . Let $F$ be the intersection of segments $AE$ and $CD$ , and suppose that $\triangle CFE$ is equilateral. What is $\angle ACB$ ?

$\textbf{(A)}\ 60^\circ \qquad \textbf{(B)}\ 75^\circ \qquad \textbf{(C)}\ 90^\circ \qquad \textbf{(D)}\ 105^\circ \qquad \textbf{(E)}\ 120^\circ$

Solution

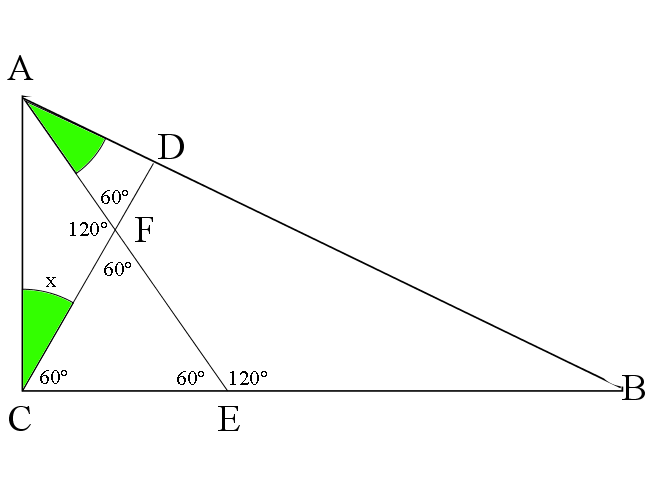
$[asy] pair A,B,C,D,E,F,G,H; G=(0,10); A=(0,3.464); B=(6,0); C=(0,0); draw(A--B--C--cycle); F=(1,1.73); E=(2,0); draw(C--F--E); D=(1.5,2.6); draw(C--D); label("$A$",A,W); label("$B$",B,S); label("$C$",C,S); label("$F$",F,N); label("$D$",D,NE); label("$E$",E,S); draw(A--E); draw(anglemark(E,A,B)); draw(anglemark(D,C,A)); [/asy]$

Let $\angle BAE = \angle ACD = x$ .

$\begin{align*}\angle BCD &= \angle AEC = 60^\circ\\ \angle EAC + \angle FCA + \angle ECF + \angle AEC &= \angle EAC + x + 60^\circ + 60^\circ = 180^\circ\\ \angle EAC &= 60^\circ - x\\ \angle BAC &= \angle EAC + \angle BAE = 60^\circ - x + x = 60^\circ\end{align*}$

Since $\frac{AC}{AB} = \frac{1}{2}$ , $\angle BCA = \boxed{90^\circ\ \textbf{(C)}}$

2010 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 13	Followed by Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.

@@ Line 5: / Line 5: @@
 == Solution ==
+<center>[[File:AMC 2010 12A Problem 8.png]]</center>
 <asy>
 pair A,B,C,D,E,F,G,H;

Page

Toolbox

Search

Difference between revisions of "2010 AMC 10A Problems/Problem 14"

Revision as of 13:38, 13 August 2017

Problem

Solution

See also