Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2004 AMC 12A Problems/Problem 18"

m (→‎Solution 5)
(→‎Solution 2)
Line 53: Line 53:
  
 
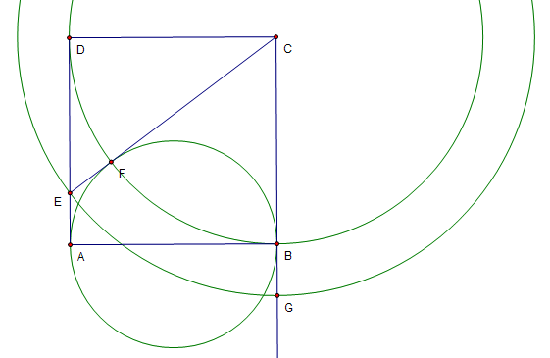
== Solution 2 ==
 
== Solution 2 ==
−
Call the point of tangency point <math>F</math> and the midpoint of <math>AB</math> as <math>G</math>. <math>CF=2</math> by the pythagorean theorem. Notice that <math>\angle EGF=\frac{180-2\cdot\angle CGF}{2}=90-\angle CGF</math>. Thus, <math>EF=\cot \theta=\frac{1}{2}</math>. Adding, the answer is <math>\frac{5}{2}</math>.
+
Call the point of tangency point <math>F</math> and the midpoint of <math>AB</math> as <math>G</math>. <math>CF=2</math> by Tangent Theorem. Notice that <math>\angle EGF=\frac{180-2\cdot\angle CGF}{2}=90-\angle CGF</math>. Thus, <math>\angle EGF=\angle FCG</math> and <math>tanEGF=tanFCG=\frac{1}{2}</math>. Solving <math>ER=\frac{1}{2}</math>. Adding, the answer is <math>\frac{5}{2}</math>.
  
 
== Solution 3 ==
 
== Solution 3 ==

Revision as of 19:58, 1 February 2018

The following problem is from both the 2004 AMC 12A #18 and 2004 AMC 10A #22, so both problems redirect to this page.

Problem

Square $ABCD$ has side length $2$. A semicircle with diameter $\overline{AB}$ is constructed inside the square, and the tangent to the semicircle from $C$ intersects side $\overline{AD}$ at $E$. What is the length of $\overline{CE}$?

[asy] size(100); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180)); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); [/asy]

$\mathrm{(A) \ } \frac{2+\sqrt{5}}{2} \qquad \mathrm{(B) \ } \sqrt{5} \qquad \mathrm{(C) \ } \sqrt{6} \qquad \mathrm{(D) \ } \frac{5}{2} \qquad \mathrm{(E) \ } 5-\sqrt{5}$

Solution 1

[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2; draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); [/asy] Let the point of tangency be $F$. By the Two Tangent Theorem $BC = FC = 2$ and $AE = EF = x$. Thus $DE = 2-x$. The Pythagorean Theorem on $\triangle CDE$ yields

\begin{align*} DE^2 + CD^2 &= CE^2\\ (2-x)^2 + 2^2 &= (2+x)^2\\ x^2 - 4x + 8 &= x^2 + 4x + 4\\ x &= \frac{1}{2}\end{align*}

Hence $CE = FC + x = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}$.


Solution 2

Call the point of tangency point $F$ and the midpoint of $AB$ as $G$. $CF=2$ by Tangent Theorem. Notice that $\angle EGF=\frac{180-2\cdot\angle CGF}{2}=90-\angle CGF$. Thus, $\angle EGF=\angle FCG$ and $tanEGF=tanFCG=\frac{1}{2}$. Solving $ER=\frac{1}{2}$. Adding, the answer is $\frac{5}{2}$.

Solution 3

2004 AMC12A-18.png

Clearly, $EA = EF = BG$. Thus, the sides of right triangle $CDE$ are in arithmetic progression. Thus it is similar to the triangle $3 - 4 - 5$ and since $DC = 2$, $CE = 5/2$.

Solution 4

[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2, G=(1,0); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); label("$G$",G,(0,-1)); dot(G); draw(G--C); label("$\sqrt{5}$",(G+C)/2,(-1,0)); [/asy]

Let us call the midpoint of side $AB$, point $G$. Since the semicircle has radius 1, we can do the Pythagorean theorem on sides $GB, BC, GC$. We get $GC=\sqrt{5}$. We then know that $CF=2$ by Pythagorean theorem. Then by connecting $EG$, we get similar triangles $EFG$ and $GFC$. Solving the ratios, we get $x=\frac{1}{2}$, so the answer is $\frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}$.

  • Solution by $AOPS12142015$

Solution 5

Using the diagram as drawn in Solution 5, let the total area of square $ABCD$ be divided into the triangles $DCE$, $EAG$, $CGB$, and $EGC$. Let x be the length of AE. Thus, the area of each triangle can be determined as follows:

\[DCE = \frac{DC\cdot{DE}}{2} = \frac{2\cdot(2-x)}{2} = 1-x\]

\[EAG= \frac{AE\cdot{AG}}{2} = \frac{1\cdot{x}}{2} = \frac{x}{2}\]

\[CGB = \frac{GB\cdot{CB}}{2} = \frac{1\cdot(2)}{2} = 1\]

\[EGC= \frac{EG\cdot{GC}}{2} = \frac{\sqrt{4+(2-x)^2}}{2}\] (the length of CE is calculated with the Pythagorean Theorem, lines GE and CE are perpendicular by definition of tangent)

Adding up the areas and equating to the area of the total square (2*2=4), we get

\[1-x+\frac{x}{2}+1+ \frac{\sqrt{4+(2-x)^2}}{2} = 4\]

Solving for x:

\[2-2x+x+1+\sqrt{x^2-4x+8}=8\] \[\sqrt{x^2-4x+8}=x+2\] \[x^2-4x+8=x^2+4x+4\] \[8-4x=4x+4 \rightarrow x=\frac{1}{2}\]

Solving for length of CE with the value we have for x: \[\sqrt{4+(2-x)^2} = \sqrt{4+(3/2)^2} = \sqrt{25/4} = \boxed{\frac{5}{2}}\]

See also

2004 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 17 		Followed by
Problem 19
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
2004 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2004_AMC_12A_Problems/Problem_18&oldid=90131"