Difference between revisions of "2002 AMC 12B Problems/Problem 18"
(→Solution 2) |
(→Solution 2) |
||
| Line 18: | Line 18: | ||
=== Solution 2 === | === Solution 2 === | ||
| − | Assume that | + | Assume that the point <math>P</math> is randomly chosen inside the rectangle with vertices <math>(0,0)</math>, <math>(3,0)</math>, <math>(3,1)</math>, <math>(0,1)</math>. |
| − | In this case, the probability that <math>P</math> is closer to the origin than to point <math>(3,1)</math> is <math>\frac{1}{2}</math>. | + | In this case, the probability that <math>P</math> is closer to the origin than to point <math>(3,1)</math> is exactly <math>\frac{1}{2}</math>. |
| − | If <math>P</math> is chosen within the square with vertices | + | If <math>P</math> is chosen within the square with vertices <math>(2,0)</math>, <math>(3,0)</math>, <math>(3,1)</math>, <math>(2,1)</math>, it is closer to <math>(3,1)</math> because the longest distance to $( |
== See also == | == See also == | ||
Revision as of 17:03, 2 July 2019
Contents
[hide]Problem
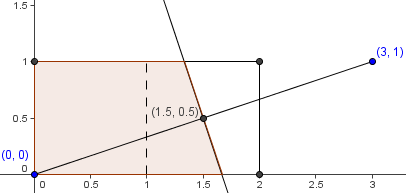
A point ![]() is randomly selected from the rectangular region with vertices
is randomly selected from the rectangular region with vertices ![]() . What is the probability that
. What is the probability that ![]() is closer to the origin than it is to the point
is closer to the origin than it is to the point ![]() ?
?
![]()
Solution
Solution 1
The region containing the points closer to ![]() than to
than to ![]() is bounded by the perpendicular bisector of the segment with endpoints
is bounded by the perpendicular bisector of the segment with endpoints ![]() . The perpendicular bisector passes through midpoint of
. The perpendicular bisector passes through midpoint of ![]() , which is
, which is ![]() , the center of the unit square with coordinates
, the center of the unit square with coordinates ![]() . Thus, it cuts the unit square into two equal halves of area
. Thus, it cuts the unit square into two equal halves of area ![]() . The total area of the rectangle is
. The total area of the rectangle is ![]() , so the area closer to the origin than to
, so the area closer to the origin than to ![]() and in the rectangle is
and in the rectangle is ![]() . The probability is
. The probability is ![]() .
.
Solution 2
Assume that the point ![]() is randomly chosen inside the rectangle with vertices
is randomly chosen inside the rectangle with vertices ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
In this case, the probability that ![]() is closer to the origin than to point
is closer to the origin than to point ![]() is exactly
is exactly ![]() .
.
If ![]() is chosen within the square with vertices
is chosen within the square with vertices ![]() ,
, ![]() ,
, ![]() ,
, ![]() , it is closer to
, it is closer to ![]() because the longest distance to $(
because the longest distance to $(
See also
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 17 |
Followed by Problem 19 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()