2002 AMC 12B Problems/Problem 20
- The following problem is from both the 2002 AMC 12B #20 and 2002 AMC 10B #22, so both problems redirect to this page.
Contents
[hide]Problem
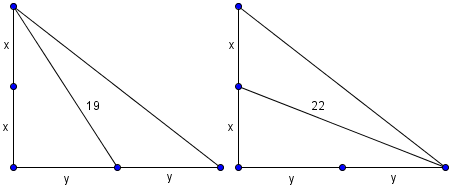
Let ![]() be a right-angled triangle with
be a right-angled triangle with ![]() . Let
. Let ![]() and
and ![]() be the midpoints of legs
be the midpoints of legs ![]() and
and ![]() , respectively. Given that
, respectively. Given that ![]() and
and ![]() , find
, find ![]() .
.
![]()
Solution 1
Let ![]() ,
, ![]() . By the Pythagorean Theorem on
. By the Pythagorean Theorem on ![]() respectively,
respectively,
![]()
Summing these gives ![]() .
.
By the Pythagorean Theorem again, we have
![]()
Alternatively, we could note that since we found ![]() , segment
, segment ![]() . Right triangles
. Right triangles ![]() and
and ![]() are similar by Leg-Leg with a ratio of
are similar by Leg-Leg with a ratio of ![]() , so
, so ![]()
Solution 2
Let ![]() and
and ![]() Then,
Then, ![]()
Since ![]() and
and ![]()
![]()
![]()
Adding these up:
![]()
![]()
![]()
![]()
Then, we substitute: ![]()
Solution 3 (Solution 1 but shorter)
Refer to the diagram in solution 1. ![]() and
and ![]() , so add them:
, so add them: ![]() and divide by 5:
and divide by 5: ![]() so
so ![]() and so
and so ![]() , or answer
, or answer ![]() .
.
Solution 4
Use the diagram in solution 1. Get ![]() and
and ![]() , and multiply the second equation by 4 to get
, and multiply the second equation by 4 to get ![]() and then subtract the first from the second. Get
and then subtract the first from the second. Get ![]() and
and ![]() . Repeat for the other variable to get
. Repeat for the other variable to get ![]() and
and ![]() . Now XY is equal to the square root of four times these quantities, so
. Now XY is equal to the square root of four times these quantities, so ![]() , and
, and ![]()
Solution 5 (Quick and good for in - contest use)
Let ![]() , and
, and ![]() . Now, we can write some equations. We have that
. Now, we can write some equations. We have that ![]() , and
, and ![]() . Adding the
. Adding the ![]() equations up we get
equations up we get ![]() . The hypotenuse of the triangle is equal to
. The hypotenuse of the triangle is equal to ![]() , so that is what we want. In order to get
, so that is what we want. In order to get ![]() , we need to subtract
, we need to subtract ![]() from
from ![]() , and since
, and since ![]() . we have that
. we have that ![]() . Therefore, the hypotenuse is
. Therefore, the hypotenuse is ![]()
-jb2015007
Video Solution by OmegaLearn
https://youtu.be/BIyhEjVp0iM?t=174
~ pi_is_3.14
Video Solution
https://www.youtube.com/watch?v=7wj6RupkO90 ~David
See also
| 2002 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()