Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
GET READY FOR THE AMC 12 WITH AoPS
Learn with outstanding instructors and top-scoring students from around the world in our AMC 12 Problem Series online course.
CHECK SCHEDULE

Difference between revisions of "2003 AMC 12A Problems"

(added problems 1-8, 12-13, 15, and 18)
m
Line 4: Line 4:
 
<math> \mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 1\qquad \mathrm{(C) \ } 2\qquad \mathrm{(D) \ } 2003\qquad \mathrm{(E) \ } 4006 </math>
 
<math> \mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 1\qquad \mathrm{(C) \ } 2\qquad \mathrm{(D) \ } 2003\qquad \mathrm{(E) \ } 4006 </math>
  
−
[[2003 AMC 12A/Problem 1|Solution]]
+
[[2003 AMC 12A Problems/Problem 1|Solution]]
  
 
== Problem 2 ==
 
== Problem 2 ==
Line 11: Line 11:
 
<math> \mathrm{(A) \ } 77\qquad \mathrm{(B) \ } 91\qquad \mathrm{(C) \ } 143\qquad \mathrm{(D) \ } 182\qquad \mathrm{(E) \ } 286 </math>
 
<math> \mathrm{(A) \ } 77\qquad \mathrm{(B) \ } 91\qquad \mathrm{(C) \ } 143\qquad \mathrm{(D) \ } 182\qquad \mathrm{(E) \ } 286 </math>
  
−
[[2003 AMC 12A/Problem 2|Solution]]
+
[[2003 AMC 12A Problems/Problem 2|Solution]]
  
 
== Problem 3 ==
 
== Problem 3 ==
Line 18: Line 18:
 
<math> \mathrm{(A) \ } 4.5\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 18\qquad \mathrm{(E) \ } 24 </math>
 
<math> \mathrm{(A) \ } 4.5\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 18\qquad \mathrm{(E) \ } 24 </math>
  
−
[[2003 AMC 12A/Problem 3|Solution]]
+
[[2003 AMC 12A Problems/Problem 3|Solution]]
  
 
== Problem 4 ==
 
== Problem 4 ==
Line 25: Line 25:
 
<math> \mathrm{(A) \ } 3\qquad \mathrm{(B) \ } 3.125\qquad \mathrm{(C) \ } 3.5\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 4.5 </math>
 
<math> \mathrm{(A) \ } 3\qquad \mathrm{(B) \ } 3.125\qquad \mathrm{(C) \ } 3.5\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 4.5 </math>
  
−
[[2003 AMC 12A/Problem 4|Solution]]
+
[[2003 AMC 12A Problems/Problem 4|Solution]]
  
 
== Problem 5 ==
 
== Problem 5 ==
Line 32: Line 32:
 
<math> \mathrm{(A) \ } 10\qquad \mathrm{(B) \ } 11\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 13\qquad \mathrm{(E) \ } 14 </math>
 
<math> \mathrm{(A) \ } 10\qquad \mathrm{(B) \ } 11\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 13\qquad \mathrm{(E) \ } 14 </math>
  
−
[[2003 AMC 12A/Problem 5|Solution]]
+
[[2003 AMC 12A Problems/Problem 5|Solution]]
  
 
== Problem 6 ==
 
== Problem 6 ==
Line 47: Line 47:
 
<math> \mathrm{(E) \ } x \heartsuit y > 0 </math> if <math>x \neq y</math>  
 
<math> \mathrm{(E) \ } x \heartsuit y > 0 </math> if <math>x \neq y</math>  
  
−
[[2003 AMC 12A/Problem 6|Solution]]
+
[[2003 AMC 12A Problems/Problem 6|Solution]]
  
 
== Problem 7 ==
 
== Problem 7 ==
Line 54: Line 54:
 
<math> \mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } 3\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 5 </math>
 
<math> \mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } 3\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 5 </math>
  
−
[[2003 AMC 12A/Problem 7|Solution]]
+
[[2003 AMC 12A Problems/Problem 7|Solution]]
  
 
== Problem 8 ==
 
== Problem 8 ==
Line 61: Line 61:
 
<math> \mathrm{(A) \ } \frac{1}{10}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{1}{4}\qquad \mathrm{(D) \ } \frac{1}{3}\qquad \mathrm{(E) \ } \frac{1}{2} </math>
 
<math> \mathrm{(A) \ } \frac{1}{10}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{1}{4}\qquad \mathrm{(D) \ } \frac{1}{3}\qquad \mathrm{(E) \ } \frac{1}{2} </math>
  
−
[[2003 AMC 12A/Problem 8|Solution]]
+
[[2003 AMC 12A Problems/Problem 8|Solution]]
  
 
== Problem 9 ==
 
== Problem 9 ==
  
−
[[2003 AMC 12A/Problem 9|Solution]]
+
[[2003 AMC 12A Problems/Problem 9|Solution]]
  
 
== Problem 10 ==
 
== Problem 10 ==
  
−
[[2003 AMC 12A/Problem 10|Solution]]
+
[[2003 AMC 12A Problems/Problem 10|Solution]]
  
 
== Problem 11 ==
 
== Problem 11 ==
  
−
[[2003 AMC 12A/Problem 11|Solution]]
+
[[2003 AMC 12A Problems/Problem 11|Solution]]
  
 
== Problem 12 ==
 
== Problem 12 ==
Line 80: Line 80:
 
<math> \mathrm{(A) \ } 8\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 10\qquad \mathrm{(D) \ } 11\qquad \mathrm{(E) \ } 12 </math>
 
<math> \mathrm{(A) \ } 8\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 10\qquad \mathrm{(D) \ } 11\qquad \mathrm{(E) \ } 12 </math>
  
−
[[2003 AMC 12A/Problem 12|Solution]]
+
[[2003 AMC 12A Problems/Problem 12|Solution]]
  
 
== Problem 13 ==
 
== Problem 13 ==
Line 89: Line 89:
 
<math> \mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 5\qquad \mathrm{(E) \ } 6 </math>
 
<math> \mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 5\qquad \mathrm{(E) \ } 6 </math>
  
−
[[2003 AMC 12A/Problem 13|Solution]]
+
[[2003 AMC 12A Problems/Problem 13|Solution]]
  
 
== Problem 14 ==
 
== Problem 14 ==
  
−
[[2003 AMC 12A/Problem 14|Solution]]
+
[[2003 AMC 12A Problems/Problem 14|Solution]]
  
 
== Problem 15 ==
 
== Problem 15 ==
Line 102: Line 102:
 
<math> \mathrm{(A) \ } \frac{1}{6}\pi-\frac{\sqrt{3}}{4}\qquad \mathrm{(B) \ } \frac{\sqrt{3}}{4}-\frac{1}{12}\pi\qquad \mathrm{(C) \ } \frac{\sqrt{3}}{4}-\frac{1}{24}\pi\qquad \mathrm{(D) \ } \frac{\sqrt{3}}{4}+\frac{1}{24}\pi\qquad \mathrm{(E) \ } \frac{\sqrt{3}}{4}+\frac{1}{12}\pi </math>
 
<math> \mathrm{(A) \ } \frac{1}{6}\pi-\frac{\sqrt{3}}{4}\qquad \mathrm{(B) \ } \frac{\sqrt{3}}{4}-\frac{1}{12}\pi\qquad \mathrm{(C) \ } \frac{\sqrt{3}}{4}-\frac{1}{24}\pi\qquad \mathrm{(D) \ } \frac{\sqrt{3}}{4}+\frac{1}{24}\pi\qquad \mathrm{(E) \ } \frac{\sqrt{3}}{4}+\frac{1}{12}\pi </math>
  
−
[[2003 AMC 12A/Problem 15|Solution]]
+
[[2003 AMC 12A Problems/Problem 15|Solution]]
  
 
== Problem 16 ==
 
== Problem 16 ==
  
−
[[2003 AMC 12A/Problem 16|Solution]]
+
[[2003 AMC 12A Problems/Problem 16|Solution]]
  
 
== Problem 17 ==
 
== Problem 17 ==
  
−
[[2003 AMC 12A/Problem 17|Solution]]
+
[[2003 AMC 12A Problems/Problem 17|Solution]]
  
 
== Problem 18 ==
 
== Problem 18 ==
Line 117: Line 117:
 
<math> \mathrm{(A) \ } 8180\qquad \mathrm{(B) \ } 8181\qquad \mathrm{(C) \ } 8182\qquad \mathrm{(D) \ } 9000\qquad \mathrm{(E) \ } 9090 </math>
 
<math> \mathrm{(A) \ } 8180\qquad \mathrm{(B) \ } 8181\qquad \mathrm{(C) \ } 8182\qquad \mathrm{(D) \ } 9000\qquad \mathrm{(E) \ } 9090 </math>
  
−
[[2003 AMC 12A/Problem 18|Solution]]
+
[[2003 AMC 12A Problems/Problem 18|Solution]]
  
 
== Problem 19 ==
 
== Problem 19 ==
  
−
[[2003 AMC 12A/Problem 19|Solution]]
+
[[2003 AMC 12A Problems/Problem 19|Solution]]
  
 
== Problem 20 ==
 
== Problem 20 ==
  
−
[[2003 AMC 12A/Problem 20|Solution]]
+
[[2003 AMC 12A Problems/Problem 20|Solution]]
  
 
== Problem 21 ==
 
== Problem 21 ==
  
−
[[2003 AMC 12A/Problem 21|Solution]]
+
[[2003 AMC 12A Problems/Problem 21|Solution]]
  
 
== Problem 22 ==
 
== Problem 22 ==
  
−
[[2003 AMC 12A/Problem 22|Solution]]
+
[[2003 AMC 12A Problems/Problem 22|Solution]]
  
 
== Problem 23 ==
 
== Problem 23 ==
  
−
[[2003 AMC 12A/Problem 23|Solution]]
+
[[2003 AMC 12A Problems/Problem 23|Solution]]
  
 
== Problem 24 ==
 
== Problem 24 ==
  
−
[[2003 AMC 12A/Problem 24|Solution]]
+
[[2003 AMC 12A Problems/Problem 24|Solution]]
  
 
== Problem 25 ==
 
== Problem 25 ==
  
−
[[2003 AMC 12A/Problem 25|Solution]]
+
[[2003 AMC 12A Problems/Problem 25|Solution]]
  
 
== See also ==
 
== See also ==

Revision as of 17:45, 17 November 2006

Problem 1

What is the difference between the sum of the first $2003$ even counting numbers and the sum of the first $2003$ odd counting numbers?

$\mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 1\qquad \mathrm{(C) \ } 2\qquad \mathrm{(D) \ } 2003\qquad \mathrm{(E) \ } 4006$

Solution

Problem 2

Members of the Rockham Soccer Leauge buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the Leauge?

$\mathrm{(A) \ } 77\qquad \mathrm{(B) \ } 91\qquad \mathrm{(C) \ } 143\qquad \mathrm{(D) \ } 182\qquad \mathrm{(E) \ } 286$

Solution

Problem 3

A solid box is $15$ cm by $10$ cm by $8$ cm. A new solid is formed by removing a cube $3$ cm on a side from each corner of this box. What percent of the original volume is removed?

$\mathrm{(A) \ } 4.5\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 18\qquad \mathrm{(E) \ } 24$

Solution

Problem 4

It takes Mary $30$ minutes to walk uphill $1$ km from her home to school, but it takes her only $10$ minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?

$\mathrm{(A) \ } 3\qquad \mathrm{(B) \ } 3.125\qquad \mathrm{(C) \ } 3.5\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 4.5$

Solution

Problem 5

The sum of the two 5-digit numbers $AMC10$ and $AMC12$ is $123422$. What is $A+M+C$?

$\mathrm{(A) \ } 10\qquad \mathrm{(B) \ } 11\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 13\qquad \mathrm{(E) \ } 14$

Solution

Problem 6

Define $x \heartsuit y$ to be $|x-y|$ for all real numbers $x$ and $y$. Which of the following statements is not true?

$\mathrm{(A) \ } x \heartsuit y = y \heartsuit x$ for all $x$ and $y$

$\mathrm{(B) \ } 2(x \heartsuit y) = (2x) \heartsuit (2y)$ for all $x$ and $y$

$\mathrm{(C) \ } x \heartsuit 0 = x$ for all $x$

$\mathrm{(D) \ } x \heartsuit x = 0$ for all $x$

$\mathrm{(E) \ } x \heartsuit y > 0$ if $x \neq y$

Solution

Problem 7

How many non-congruent triangles with perimeter $7$ have integer side lengths?

$\mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } 3\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 5$

Solution

Problem 8

What is the probability that a randomly drawn positive factor of $60$ is less than $7$

$\mathrm{(A) \ } \frac{1}{10}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{1}{4}\qquad \mathrm{(D) \ } \frac{1}{3}\qquad \mathrm{(E) \ } \frac{1}{2}$

Solution

Problem 9

Solution

Problem 10

Solution

Problem 11

Solution

Problem 12

Sally has five red cards numbered $1$ through $5$ and four blue cards numbered $3$ through $6$. She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?

$\mathrm{(A) \ } 8\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 10\qquad \mathrm{(D) \ } 11\qquad \mathrm{(E) \ } 12$

Solution

Problem 13

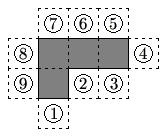
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attatched to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?

2003amc10a10.gif

$\mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 5\qquad \mathrm{(E) \ } 6$

Solution

Problem 14

Solution

Problem 15

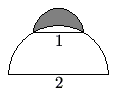
A semicircle of diameter $1$ sits at the top of a semicircle of diameter $2$, as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.

2003amc10a19.gif

$\mathrm{(A) \ } \frac{1}{6}\pi-\frac{\sqrt{3}}{4}\qquad \mathrm{(B) \ } \frac{\sqrt{3}}{4}-\frac{1}{12}\pi\qquad \mathrm{(C) \ } \frac{\sqrt{3}}{4}-\frac{1}{24}\pi\qquad \mathrm{(D) \ } \frac{\sqrt{3}}{4}+\frac{1}{24}\pi\qquad \mathrm{(E) \ } \frac{\sqrt{3}}{4}+\frac{1}{12}\pi$

Solution

Problem 16

Solution

Problem 17

Solution

Problem 18

Let $n$ be a $5$-digit number, and let $q$ and $r$ be the quotient and the remainder, respectively, when $n$ is divided by $100$. For how many values of $n$ is $q+r$ divisible by $11$?

$\mathrm{(A) \ } 8180\qquad \mathrm{(B) \ } 8181\qquad \mathrm{(C) \ } 8182\qquad \mathrm{(D) \ } 9000\qquad \mathrm{(E) \ } 9090$

Solution

Problem 19

Solution

Problem 20

Solution

Problem 21

Solution

Problem 22

Solution

Problem 23

Solution

Problem 24

Solution

Problem 25

Solution

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12A_Problems&oldid=11792"