Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 Cyprus MO/Lyceum/Problems"

(→‎Problem 6)
(→‎Problem 7)
Line 98: Line 98:
 
[[Image:2006 CyMO-7.PNG|250px]]
 
[[Image:2006 CyMO-7.PNG|250px]]
 
</div>
 
</div>
 +
 +
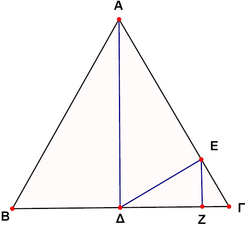
In the figure, <math>ABC</math> is an equilateral triangle and <math>AD\perp BC</math>, <math>DE\perp AC</math>, <math>EZ\perp BC</math>. If <math>EZ=\sqrt{3}</math>, then the length of the side os the triangle ABC is
 +
 +
 +
A. <math>\frac{3\sqrt{3}}{2}</math>
 +
 +
B. <math>8</math>
 +
 +
C.  <math>4</math>
 +
 +
D. <math>3</math>
 +
 +
E. <math>9</math>
  
 
[[2006 Cyprus MO/Lyceum/Problem 7|Solution]]
 
[[2006 Cyprus MO/Lyceum/Problem 7|Solution]]

Revision as of 09:41, 30 June 2007

Problem 1

A diary industry, in a quantity of milk with $4%$ (Error compiling LaTeX. Unknown error_msg) fat adds a quantity of milk with $1%$ (Error compiling LaTeX. Unknown error_msg) fat and produces $1200$kg of milk with $2%$ (Error compiling LaTeX. Unknown error_msg) fat. The quantity of milk with $1%$ (Error compiling LaTeX. Unknown error_msg) fat, that was added is (in kg)

A. $1000$

B. $600$

C. $800$

D. $120$

E. $480$

Solution

Problem 2

The operation $\alpha * \beta$ is defined by $\alpha * \beta = \alpha^2 - \beta^2$ $\forall \alpha , \beta \in R$. The value of the expression $K = \left[\left(1+\sqrt{3}\right) * 2\right]*\sqrt{2}$ is

A. $3$

B. $0$

C. $\sqrt{3}$

D. $9$

E. $1$

Solution

Problem 3

The domain of the function $f(x)=\sqrt{4+2x}$ is

A. $(-2,+\infty)$

B. $[0,+\infty)$

C. $[-2,+\infty)$

D. $[-2,0]$

E. $R$

Solution

Problem 4

Given the function $f(x)=\alpha x^2 +9x+ \frac{81}{4\alpha}$ , $\alpha \neq 0$ Which of the following is correct, about the graph of $f$?


A. intersects x-axis

B. touches y-axis

C. touches x-axis

D. has minimum point

E. has maximum point

Solution

Problem 5

If both integers $\alpha,\beta$ are bigger than 1 and satisfy $a^7=b^8$, then the minimum value of $\alpha+\beta$ is

A. $384$

B. $2$

C. $15$

D. $56$

E. $512$

Solution

Problem 6

The value of the expression $K=\sqrt{19+7\sqrt{3}}-\sqrt{7+4\sqrt{3}}$ is


A. $4$

B. $4\sqrt{3}$

C. $12+4\sqrt{3}$

D. $-2$

E. $2$

Solution

Problem 7

2006 CyMO-7.PNG

In the figure, $ABC$ is an equilateral triangle and $AD\perp BC$, $DE\perp AC$, $EZ\perp BC$. If $EZ=\sqrt{3}$, then the length of the side os the triangle ABC is


A. $\frac{3\sqrt{3}}{2}$

B. $8$

C. $4$

D. $3$

E. $9$

Solution

Problem 8

2006 CyMO-8.PNG

Solution

Problem 9

Solution

Problem 10

Solution

Problem 11

2006 CyMO-11.PNG


Solution

Problem 12

Solution

Problem 13

Solution

Problem 14

2006 CyMO-17.PNG


Solution

Problem 15

Solution

Problem 16

Solution

Problem 17

2006 CyMO-17.PNG


Solution

Problem 18

2006 CyMO-18.PNG


Solution

Problem 19

2006 CyMO-19.PNG


Solution

Problem 20

Solution

Problem 21

Solution

Problem 22

2006 CyMO-22.PNG


Solution

Problem 23

Solution

Problem 24

Solution

Problem 25

Solution

Problem 26

Solution

Problem 27

Solution

Problem 28

Solution

Problem 29

Solution

Problem 30

Solution

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_Cyprus_MO/Lyceum/Problems&oldid=15263"