Difference between revisions of "2007 AMC 12A Problems/Problem 6"
(→See also) |
(diagram, wik) |
||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
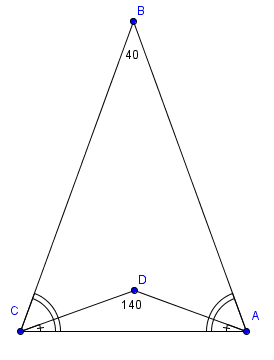
| − | Triangles ABC and ADC are isosceles with AB=BC and AD=DC. Point D is inside triangle ABC, angle ABC measures 40 degrees, and angle ADC measures 140 degrees. What is the degree measure of angle BAD? | + | Triangles <math>ABC</math> and <math>ADC</math> are [[isosceles]] with <math>AB=BC</math> and <math>\displaystyle AD=DC</math>. Point <math>D</math> is inside triangle <math>ABC</math>, angle <math>ABC</math> measures 40 degrees, and angle <math>ADC</math> measures 140 degrees. What is the degree measure of angle <math>BAD</math>? |
| + | |||
| + | <math>\mathrm{(A)}\ 20\qquad \mathrm{(B)}\ 30\qquad \mathrm{(C)}\ 40\qquad \mathrm{(D)}\ 50\qquad \mathrm{(E)}\ 60</math> | ||
==Solution== | ==Solution== | ||
| − | + | [[Image:2007_AMC12A-6.png]] | |
| − | + | ||
| − | * DAC=20 | + | We angle chase, and find out that: |
| − | * BAC=70 | + | * <math>DAC=\frac{180-140}{2} = 20</math> |
| − | * BAD=50 | + | * <math>BAC=\frac{180-40}{2} = 70</math> |
| + | * <math>BAD=BAC-DAC=50\ \mathrm{(A)}</math> | ||
==See also== | ==See also== | ||
| − | + | {{AMC12 box|year=2007|ab=A|num-b=5|num-a=7}} | |
| − | + | ||
| − | + | [[Category:Introductory Geometry Problems]] | |
Revision as of 11:00, 9 September 2007
Problem
Triangles 
and 
are isosceles with 
and 
. Point 
is inside triangle , angle measures 40 degrees, and angle measures 140 degrees. What is the degree measure of angle 
?
Solution
We angle chase, and find out that:
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 5 |
Followed by Problem 7 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
