Difference between revisions of "2005 AMC 12A Problems/Problem 7"
(solution) |
m (img 2) |
||
| Line 6: | Line 6: | ||
</math> | </math> | ||
== Solution == | == Solution == | ||
| + | [[Image:2005_12A_AMC-7b.png]] | ||
| + | |||
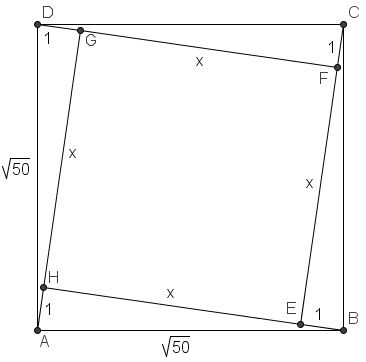
Arguable the hardest part of this question is to visualize the diagram. Since each side of <math>EFGH</math> can be extended to pass through a vertex of <math>ABCD</math>, we realize that <math>EFGH</math> must be tilted in such a fashion. Let a side of <math>EFGH</math> be <math>x</math>. | Arguable the hardest part of this question is to visualize the diagram. Since each side of <math>EFGH</math> can be extended to pass through a vertex of <math>ABCD</math>, we realize that <math>EFGH</math> must be tilted in such a fashion. Let a side of <math>EFGH</math> be <math>x</math>. | ||
Revision as of 12:47, 23 September 2007
Problem
Square ![]() is inside the square
is inside the square ![]() so that each side of
so that each side of ![]() can be extended to pass through a vertex of
can be extended to pass through a vertex of ![]() . Square
. Square ![]() has side length
has side length ![]() and
and ![]() . What is the area of the inner square
. What is the area of the inner square ![]() ?
?
![]()
Solution
Arguable the hardest part of this question is to visualize the diagram. Since each side of ![]() can be extended to pass through a vertex of
can be extended to pass through a vertex of ![]() , we realize that
, we realize that ![]() must be tilted in such a fashion. Let a side of
must be tilted in such a fashion. Let a side of ![]() be
be ![]() .
.
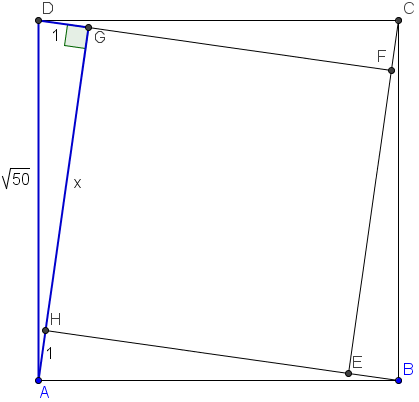
Notice the right triangle (in blue) with legs ![]() and hypotenuse
and hypotenuse ![]() . By the Pythagorean Theorem, we have
. By the Pythagorean Theorem, we have ![]() . Thus,
. Thus, ![]()
See also
| 2005 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 6 |
Followed by Problem 8 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |