Difference between revisions of "Unit circle"
| Line 23: | Line 23: | ||
{{stub}} | {{stub}} | ||
| + | |||
| + | [[Category:Geometry]] | ||
Revision as of 19:37, 14 October 2007
| This is an AoPSWiki Word of the Week for Oct 11-17 |
A unit circle is a circle whose radius has length 1.
In the Cartesian coordinate system, an equation of the form 
defines a unit circle with center 
.
Trigonometry
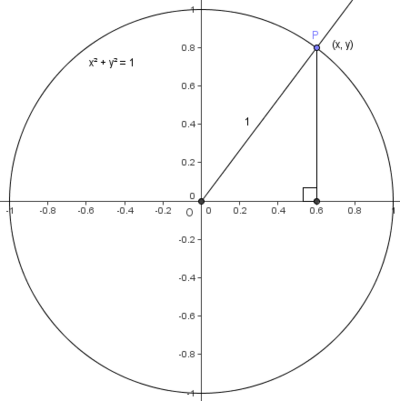
An unit circle centered at the origin can be used to calculate values for the basic trigonometric functions. Suppose we draw a ray starting from the origin and meeting the positive x-axis with an angle of 
. If we drop a perpendicular from the point of intersection between the ray and the circle, we have a right triangle with hypotenuse of 
.
Using the definitions 
and 
, we find that 
and 
.
We can read off values for sine and cosine of an angle this way; we can draw the angle and approximate the x and y coordinates of the intersection.
We can also prove one of he fundamental theorems of trigonometry: 
. The proof is as follows:
We see that the length and width of the triangle in the diagram at left are 
and 
, respectively. We use the pythagorean theorem to get:
This article is a stub. Help us out by expanding it.
