Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2001 AMC 10 Problems/Problem 5"
(→‎Problem)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
  
−
How many of the twelve pentominoes pictured below have at least one line of symmetry?
+
A <math>5\times 5 \times 5</math> cube has all its faces painted, and then is cut into <math>125</math> small cubes, each <math>1\times 1\times 1</math>. How many of these small cubes have exactly <math>2</math> of their <math>6</math> faces painted?
  
 
<asy>
 
<asy>

Revision as of 18:32, 12 November 2022

Problem

A $5\times 5 \times 5$ cube has all its faces painted, and then is cut into $125$ small cubes, each $1\times 1\times 1$. How many of these small cubes have exactly $2$ of their $6$ faces painted?

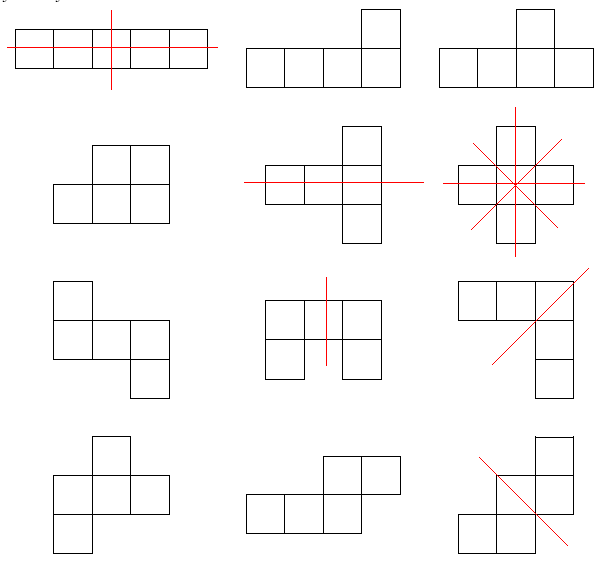
[asy] unitsize(5mm); defaultpen(linewidth(1pt)); draw(shift(2,0)*unitsquare); draw(shift(2,1)*unitsquare); draw(shift(2,2)*unitsquare); draw(shift(1,2)*unitsquare); draw(shift(0,2)*unitsquare); draw(shift(2,4)*unitsquare); draw(shift(2,5)*unitsquare); draw(shift(2,6)*unitsquare); draw(shift(1,5)*unitsquare); draw(shift(0,5)*unitsquare); draw(shift(4,8)*unitsquare); draw(shift(3,8)*unitsquare); draw(shift(2,8)*unitsquare); draw(shift(1,8)*unitsquare); draw(shift(0,8)*unitsquare); draw(shift(6,8)*unitsquare); draw(shift(7,8)*unitsquare); draw(shift(8,8)*unitsquare); draw(shift(9,8)*unitsquare); draw(shift(9,9)*unitsquare); draw(shift(6,5)*unitsquare); draw(shift(7,5)*unitsquare); draw(shift(8,5)*unitsquare); draw(shift(7,6)*unitsquare); draw(shift(7,4)*unitsquare); draw(shift(6,1)*unitsquare); draw(shift(7,1)*unitsquare); draw(shift(8,1)*unitsquare); draw(shift(6,0)*unitsquare); draw(shift(7,2)*unitsquare); draw(shift(11,8)*unitsquare); draw(shift(12,8)*unitsquare); draw(shift(13,8)*unitsquare); draw(shift(14,8)*unitsquare); draw(shift(13,9)*unitsquare); draw(shift(11,5)*unitsquare); draw(shift(12,5)*unitsquare); draw(shift(13,5)*unitsquare); draw(shift(11,6)*unitsquare); draw(shift(13,4)*unitsquare); draw(shift(11,1)*unitsquare); draw(shift(12,1)*unitsquare); draw(shift(13,1)*unitsquare); draw(shift(13,2)*unitsquare); draw(shift(14,2)*unitsquare); draw(shift(16,8)*unitsquare); draw(shift(17,8)*unitsquare); draw(shift(18,8)*unitsquare); draw(shift(17,9)*unitsquare); draw(shift(18,9)*unitsquare); draw(shift(16,5)*unitsquare); draw(shift(17,6)*unitsquare); draw(shift(18,5)*unitsquare); draw(shift(16,6)*unitsquare); draw(shift(18,6)*unitsquare); draw(shift(16,0)*unitsquare); draw(shift(17,0)*unitsquare); draw(shift(17,1)*unitsquare); draw(shift(18,1)*unitsquare); draw(shift(18,2)*unitsquare);[/asy]

$\textbf{(A)}\ 3 \qquad \textbf{(B)}\ 4 \qquad \textbf{(C)}\ 5 \qquad \textbf{(D)}\ 6 \qquad \textbf{(E)}\ 7$

Solution

Pentonimoes.gif

The ones with lines over the shapes have at least one line of symmetry. Counting the number of shapes that have line(s) on them, we find $\boxed{\textbf{(D)}\ 6}$ pentominoes.

See Also

2001 AMC 10 (Problems • Answer Key • Resources)
Preceded by
Problem 4 		Followed by
Problem 6
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2001_AMC_10_Problems/Problem_5&oldid=181181"