Difference between revisions of "2004 AMC 12A Problems/Problem 18"
m (2004 AMC 10A Problems/Problem 22 moved to 2004 AMC 12A Problems/Problem 18: {{dup}}) |
(sol, {{dup}}) |
||
| Line 1: | Line 1: | ||
| + | {{duplicate|[[2004 AMC 12A Problems|2004 AMC 12A #18]] and [[2004 AMC 10A Problems/Problem 22|2004 AMC 10A #22]]}} | ||
| + | |||
==Problem== | ==Problem== | ||
| − | Square <math>ABCD</math> has side length 2. A semicircle with diameter <math>\overline{AB}</math> is constructed inside the square, and the tangent to the semicircle from <math>C</math> intersects side <math>\overline{AD}</math> at <math>E</math>. What is the length of <math>\overline{CE}</math>? | + | [[Square]] <math>ABCD</math> has side length <math>2</math>. A [[semicircle]] with [[diameter]] <math>\overline{AB}</math> is constructed inside the square, and the [[tangent (geometry)|tangent]] to the semicircle from <math>C</math> intersects side <math>\overline{AD}</math> at <math>E</math>. What is the length of <math>\overline{CE}</math>? |
<center>[[Image:AMC10_2004A_22.png]]</center> | <center>[[Image:AMC10_2004A_22.png]]</center> | ||
| Line 6: | Line 8: | ||
<math> \mathrm{(A) \ } \frac{2+\sqrt{5}}{2} \qquad \mathrm{(B) \ } \sqrt{5} \qquad \mathrm{(C) \ } \sqrt{6} \qquad \mathrm{(D) \ } \frac{5}{2} \qquad \mathrm{(E) \ } 5-\sqrt{5} </math> | <math> \mathrm{(A) \ } \frac{2+\sqrt{5}}{2} \qquad \mathrm{(B) \ } \sqrt{5} \qquad \mathrm{(C) \ } \sqrt{6} \qquad \mathrm{(D) \ } \frac{5}{2} \qquad \mathrm{(E) \ } 5-\sqrt{5} </math> | ||
| + | __TOC__ | ||
==Solution== | ==Solution== | ||
| + | === Solution 1 === | ||
| + | Let the point of tangency be <math>F</math>. By the [[Two Tangent Theorem]] <math>BC = FC = 2</math> and <math>AE = EF = x</math>. Thus <math>DE = 2-x</math>. The [[Pythagorean Theorem]] on <math>\triangle CDE</math> yields | ||
| + | |||
| + | <cmath>\begin{eqnarray*}(2-x)^2 + 2^2 &=& (2+x)^2\\ | ||
| + | x^2 - 4x + 8 &=& x^2 + 4x + 4\\ | ||
| + | x &=& \frac{1}{2}\end{eqnarray*}</cmath> | ||
| + | |||
| + | Hence <math>CE = FC + x = \frac{5}{2} \Rightarrow \mathrm{(D)}</math>. | ||
| + | |||
| + | === Solution 2 === | ||
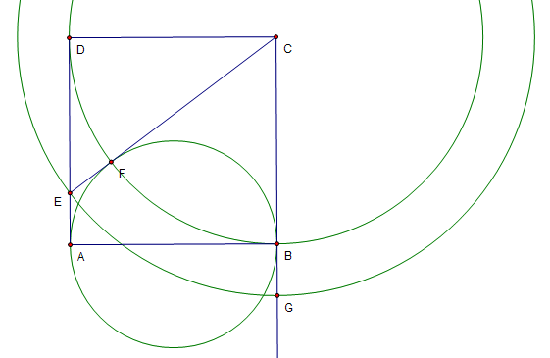
| + | [[Image:2004_AMC12A-18.png]] | ||
| + | |||
| + | Clearly, <math>EA = EF = BG</math>. Thus, the sides of [[right triangle]] <math>CDE</math> are in arithmetic progression. Thus it is [[similar triangles|similar]] to the triangle <math>3 - 4 - 5</math> and since <math>DC = 2</math>, <math>CE = 5/2</math>. | ||
| + | |||
== See also == | == See also == | ||
* [http://www.artofproblemsolving.com/Forum/viewtopic.php?t=131334 AoPS topic] | * [http://www.artofproblemsolving.com/Forum/viewtopic.php?t=131334 AoPS topic] | ||
| + | {{AMC12 box|year=2004|ab=A|num-b=17|num-a=19}} | ||
{{AMC10 box|year=2004|ab=A|num-b=21|num-a=23}} | {{AMC10 box|year=2004|ab=A|num-b=21|num-a=23}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
Revision as of 20:31, 3 December 2007
- The following problem is from both the 2004 AMC 12A #18 and 2004 AMC 10A #22, so both problems redirect to this page.
Problem
Square 
has side length 
. A semicircle with diameter 
is constructed inside the square, and the tangent to the semicircle from 
intersects side 
at 
. What is the length of 
?
Solution
Solution 1
Let the point of tangency be 
. By the Two Tangent Theorem 
and 
. Thus 
. The Pythagorean Theorem on 
yields
Hence 
.
Solution 2
Clearly, 
. Thus, the sides of right triangle 
are in arithmetic progression. Thus it is similar to the triangle 
and since 
, 
.
See also
| 2004 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 17 |
Followed by Problem 19 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2004 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
