Difference between revisions of "2024 AMC 10A Problems/Problem 22"
(→Problem) |
(→Solution) |
||
| Line 11: | Line 11: | ||
[[File:Screenshot 2024-11-08 2.33.52 PM.png]] | [[File:Screenshot 2024-11-08 2.33.52 PM.png]] | ||
| + | |||
| + | Due to the many similarities present, we can find that <math>AB</math> | ||
==See also== | ==See also== | ||
{{AMC10 box|year=2024|ab=A|num-b=21|num-a=23}} | {{AMC10 box|year=2024|ab=A|num-b=21|num-a=23}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 17:39, 8 November 2024
Problem
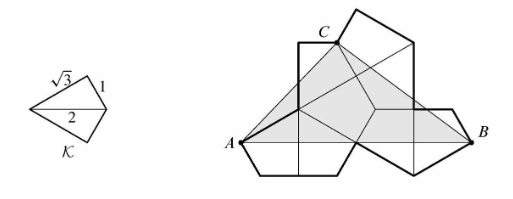
Let 
be the kite formed by joining two right triangles with legs 
and 
along a common hypotenuse. Eight copies of are used to form the polygon shown below. What is the area of triangle 
?
Solution
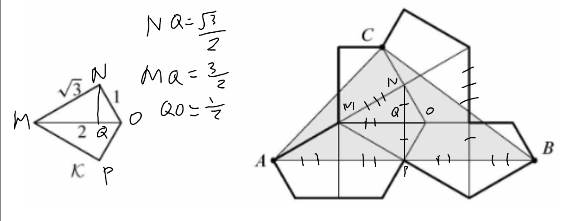
Let be quadrilateral MNOP. Drawing line MO splits the triangle into 
.
Drawing the altitude from N to point Q on line MO, we know NQ is 
, MQ is 
, and QO is 
.
Due to the many similarities present, we can find that 
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
