Difference between revisions of "2006 AMC 12A Problems"
(→Problem 1) |
I like pie (talk | contribs) (LaTeX Style) |
||
| Line 1: | Line 1: | ||
== Problem 1 == | == Problem 1 == | ||
| − | |||
Sandwiches at Joe's Fast Food cost <math>\</math>3 each and sodas cost <math>\</math>2 each. How many dollars will it cost to purchase <math>5</math> sandwiches and <math>8</math> sodas? | Sandwiches at Joe's Fast Food cost <math>\</math>3 each and sodas cost <math>\</math>2 each. How many dollars will it cost to purchase <math>5</math> sandwiches and <math>8</math> sodas? | ||
| Line 8: | Line 7: | ||
== Problem 2 == | == Problem 2 == | ||
| − | |||
Define <math>x\otimes y=x^3-y</math>. What is <math>h\otimes (h\otimes h)</math>? | Define <math>x\otimes y=x^3-y</math>. What is <math>h\otimes (h\otimes h)</math>? | ||
| Line 16: | Line 14: | ||
== Problem 3 == | == Problem 3 == | ||
| − | |||
The ratio of Mary's age to Alice's age is <math>3:5</math>. Alice is <math>30</math> years old. How old is Mary? | The ratio of Mary's age to Alice's age is <math>3:5</math>. Alice is <math>30</math> years old. How old is Mary? | ||
| Line 24: | Line 21: | ||
== Problem 4 == | == Problem 4 == | ||
| − | |||
A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display? | A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display? | ||
| Line 32: | Line 28: | ||
== Problem 5 == | == Problem 5 == | ||
| − | |||
Doug and Dave shared a pizza with <math>8</math> equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was <dollar/><math>8</math>, and there was an additional cost of <dollar/><math>2</math> for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug? | Doug and Dave shared a pizza with <math>8</math> equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was <dollar/><math>8</math>, and there was an additional cost of <dollar/><math>2</math> for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug? | ||
| Line 49: | Line 44: | ||
== Problem 7 == | == Problem 7 == | ||
| − | |||
Mary is <math>20%</math> older than Sally, and Sally is <math>40%</math> younger than Danielle. The sum of their ages is <math>23.2</math> years. How old will Mary be on her next birthday? | Mary is <math>20%</math> older than Sally, and Sally is <math>40%</math> younger than Danielle. The sum of their ages is <math>23.2</math> years. How old will Mary be on her next birthday? | ||
| Line 57: | Line 51: | ||
== Problem 8 == | == Problem 8 == | ||
| − | |||
How many sets of two or more consecutive positive integers have a sum of <math>15</math>? | How many sets of two or more consecutive positive integers have a sum of <math>15</math>? | ||
| Line 65: | Line 58: | ||
== Problem 9 == | == Problem 9 == | ||
| − | |||
Oscar buys <math>13</math> pencils and <math>3</math> erasers for <dollar/><math>1.00</math>. A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser? | Oscar buys <math>13</math> pencils and <math>3</math> erasers for <dollar/><math>1.00</math>. A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser? | ||
| Line 73: | Line 65: | ||
== Problem 10 == | == Problem 10 == | ||
| − | |||
For how many real values of <math>x</math> is <math>\sqrt{120-\sqrt{x}}</math> an integer? | For how many real values of <math>x</math> is <math>\sqrt{120-\sqrt{x}}</math> an integer? | ||
| Line 81: | Line 72: | ||
== Problem 11 == | == Problem 11 == | ||
| − | |||
Which of the following describes the graph of the equation <math>(x+y)^2=x^2+y^2</math>? | Which of the following describes the graph of the equation <math>(x+y)^2=x^2+y^2</math>? | ||
| − | <math> \mathrm{(A) | + | <math>\mathrm{(A)}\ \text{the empty set}\qquad\mathrm{(B)}\ \text{one point}\mathrm{(C)}\ \text{two lines}\qquad\mathrm{(D)}\ \text{a circle}\qquad\mathrm{(E)}\ \text{the entire plane}</math> |
[[2006 AMC 12A Problems/Problem 11|Solution]] | [[2006 AMC 12A Problems/Problem 11|Solution]] | ||
== Problem 12 == | == Problem 12 == | ||
| − | |||
{{image}} | {{image}} | ||
| Line 99: | Line 88: | ||
== Problem 13 == | == Problem 13 == | ||
| − | |||
[[Image:2006_AMC_12A_Problem_13.gif]] | [[Image:2006_AMC_12A_Problem_13.gif]] | ||
| Line 109: | Line 97: | ||
== Problem 14 == | == Problem 14 == | ||
| − | |||
Two farmers agree that pigs are worth <dollar/><math>300</math> and that goats are worth <dollar/><math>210</math>. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a <dollar/><math>390</math> debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way? | Two farmers agree that pigs are worth <dollar/><math>300</math> and that goats are worth <dollar/><math>210</math>. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a <dollar/><math>390</math> debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way? | ||
| Line 117: | Line 104: | ||
== Problem 15 == | == Problem 15 == | ||
| − | |||
Suppose <math>\cos x=0</math> and <math>\cos (x+z)=1/2</math>. What is the smallest possible positive value of <math>z</math>? | Suppose <math>\cos x=0</math> and <math>\cos (x+z)=1/2</math>. What is the smallest possible positive value of <math>z</math>? | ||
| Line 125: | Line 111: | ||
== Problem 16 == | == Problem 16 == | ||
| − | |||
Circles with centers <math>A</math> and <math>B</math> have radii <math>3</math> and <math>8</math>, respectively. A common internal tangent intersects the circles at <math>C</math> and <math>D</math>, respectively. Lines <math>AB</math> and <math>CD</math> intersect at <math>E</math>, and <math>AE=5</math>. What is <math>CD</math>? | Circles with centers <math>A</math> and <math>B</math> have radii <math>3</math> and <math>8</math>, respectively. A common internal tangent intersects the circles at <math>C</math> and <math>D</math>, respectively. Lines <math>AB</math> and <math>CD</math> intersect at <math>E</math>, and <math>AE=5</math>. What is <math>CD</math>? | ||
| − | + | [[Image:2006_AMC12A-16.png|center]] | |
<math> \mathrm{(A) \ } 13\qquad \mathrm{(B) \ } \frac{44}{3}\qquad \mathrm{(C) \ } \sqrt{221}\qquad \mathrm{(D) \ } \sqrt{255}\qquad \mathrm{(E) \ } \frac{55}{3}</math> | <math> \mathrm{(A) \ } 13\qquad \mathrm{(B) \ } \frac{44}{3}\qquad \mathrm{(C) \ } \sqrt{221}\qquad \mathrm{(D) \ } \sqrt{255}\qquad \mathrm{(E) \ } \frac{55}{3}</math> | ||
| Line 135: | Line 120: | ||
== Problem 17 == | == Problem 17 == | ||
| − | |||
Square <math>ABCD</math> has side length <math>s</math>, a circle centered at <math>E</math> has radius <math>r</math>, and <math>r</math> and <math>s</math> are both rational. The circle passes through <math>D</math>, and <math>D</math> lies on <math>\overline{BE}</math>. Point <math>F</math> lies on the circle, on the same side of <math>\overline{BE}</math> as <math>A</math>. Segment <math>AF</math> is tangent to the circle, and <math>AF=\sqrt{9+5\sqrt{2}}</math>. What is <math>r/s</math>? | Square <math>ABCD</math> has side length <math>s</math>, a circle centered at <math>E</math> has radius <math>r</math>, and <math>r</math> and <math>s</math> are both rational. The circle passes through <math>D</math>, and <math>D</math> lies on <math>\overline{BE}</math>. Point <math>F</math> lies on the circle, on the same side of <math>\overline{BE}</math> as <math>A</math>. Segment <math>AF</math> is tangent to the circle, and <math>AF=\sqrt{9+5\sqrt{2}}</math>. What is <math>r/s</math>? | ||
| − | + | [[Image:AMC12_2006A_17.png|center]] | |
<math> \mathrm{(A) \ } \frac{1}{2}\qquad \mathrm{(B) \ } \frac{5}{9}\qquad \mathrm{(C) \ } \frac{3}{5}\qquad \mathrm{(D) \ } \frac{5}{3}\qquad \mathrm{(E) \ } \frac{9}{5}</math> | <math> \mathrm{(A) \ } \frac{1}{2}\qquad \mathrm{(B) \ } \frac{5}{9}\qquad \mathrm{(C) \ } \frac{3}{5}\qquad \mathrm{(D) \ } \frac{5}{3}\qquad \mathrm{(E) \ } \frac{9}{5}</math> | ||
| Line 145: | Line 129: | ||
== Problem 18 == | == Problem 18 == | ||
| − | + | The function <math>f</math> has the property that for each real number <math>x</math> in its domain, <math>1/x</math> is also in its domain and | |
| − | The function <math> | ||
<math>f(x)+f\left(\frac{1}{x}\right)=x</math> | <math>f(x)+f\left(\frac{1}{x}\right)=x</math> | ||
| Line 157: | Line 140: | ||
== Problem 19 == | == Problem 19 == | ||
| − | |||
Circles with centers <math>(2,4)</math> and <math>(14,9)</math> have radii <math>4</math> and <math>9</math>, respectively. The equation of a common external tangent to the circles can be written in the form <math>y=mx+b</math> with <math>m>0</math>. What is <math>b</math>? | Circles with centers <math>(2,4)</math> and <math>(14,9)</math> have radii <math>4</math> and <math>9</math>, respectively. The equation of a common external tangent to the circles can be written in the form <math>y=mx+b</math> with <math>m>0</math>. What is <math>b</math>? | ||
| − | + | [[Image:AMC12_2006A_19.png|center]] | |
<math> \mathrm{(A) \ } \frac{908}{199}\qquad \mathrm{(B) \ } \frac{909}{119}\qquad \mathrm{(C) \ } \frac{130}{17}\qquad \mathrm{(D) \ } \frac{911}{119}\qquad \mathrm{(E) \ } \frac{912}{119}</math> | <math> \mathrm{(A) \ } \frac{908}{199}\qquad \mathrm{(B) \ } \frac{909}{119}\qquad \mathrm{(C) \ } \frac{130}{17}\qquad \mathrm{(D) \ } \frac{911}{119}\qquad \mathrm{(E) \ } \frac{912}{119}</math> | ||
| Line 167: | Line 149: | ||
== Problem 20 == | == Problem 20 == | ||
| − | |||
A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once? | A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once? | ||
| Line 175: | Line 156: | ||
== Problem 21 == | == Problem 21 == | ||
| − | |||
Let | Let | ||
| Line 191: | Line 171: | ||
== Problem 22 == | == Problem 22 == | ||
| − | |||
A circle of radius <math>r</math> is concentric with and outside a regular hexagon of side length <math>2</math>. The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is <math>1/2</math>. What is <math>r</math>? | A circle of radius <math>r</math> is concentric with and outside a regular hexagon of side length <math>2</math>. The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is <math>1/2</math>. What is <math>r</math>? | ||
| Line 199: | Line 178: | ||
== Problem 23 == | == Problem 23 == | ||
| − | |||
Given a finite sequence <math>S=(a_1,a_2,\ldots ,a_n)</math> of <math>n</math> real numbers, let <math>A(S)</math> be the sequence | Given a finite sequence <math>S=(a_1,a_2,\ldots ,a_n)</math> of <math>n</math> real numbers, let <math>A(S)</math> be the sequence | ||
| Line 211: | Line 189: | ||
== Problem 24 == | == Problem 24 == | ||
| − | |||
The expression | The expression | ||
| Line 223: | Line 200: | ||
== Problem 25 == | == Problem 25 == | ||
| − | + | How many non-empty subsets <math>S</math> of <math>\lbrace 1,2,3,\ldots ,15\rbrace</math> have the following two properties? | |
| − | How many non-empty subsets <math>S</math> of <math>\ | ||
<math>(1)</math> No two consecutive integers belong to <math>S</math>. | <math>(1)</math> No two consecutive integers belong to <math>S</math>. | ||
Revision as of 23:58, 27 April 2008
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
Sandwiches at Joe's Fast Food cost ![]() 3 each and sodas cost
3 each and sodas cost ![]() 2 each. How many dollars will it cost to purchase
2 each. How many dollars will it cost to purchase ![]() sandwiches and
sandwiches and ![]() sodas?
sodas?
![]()
Problem 2
Define ![]() . What is
. What is ![]() ?
?
![]()
Problem 3
The ratio of Mary's age to Alice's age is ![]() . Alice is
. Alice is ![]() years old. How old is Mary?
years old. How old is Mary?
![]()
Problem 4
A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display?
![]()
Problem 5
Doug and Dave shared a pizza with ![]() equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was <dollar/>
equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was <dollar/>![]() , and there was an additional cost of <dollar/>
, and there was an additional cost of <dollar/>![]() for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug?
for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug?
![]()
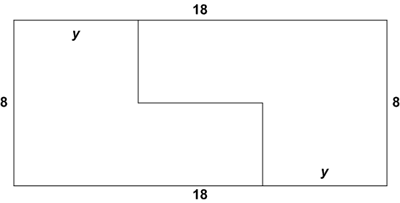
Problem 6
The ![]() rectangle
rectangle ![]() is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is
is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is ![]() ?
?
![]()
Problem 7
Mary is $20%$ (Error compiling LaTeX. Unknown error_msg) older than Sally, and Sally is $40%$ (Error compiling LaTeX. Unknown error_msg) younger than Danielle. The sum of their ages is ![]() years. How old will Mary be on her next birthday?
years. How old will Mary be on her next birthday?
![]()
Problem 8
How many sets of two or more consecutive positive integers have a sum of ![]() ?
?
![]()
Problem 9
Oscar buys ![]() pencils and
pencils and ![]() erasers for <dollar/>
erasers for <dollar/>![]() . A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser?
. A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser?
![]()
Problem 10
For how many real values of ![]() is
is ![]() an integer?
an integer?
![]()
Problem 11
Which of the following describes the graph of the equation ![]() ?
?
![]()
Problem 12
An image is supposed to go here. You can help us out by creating one and editing it in. Thanks.
A number of linked rings, each 1 cm thick, are hanging on a peg. The top ring has an outisde diameter of 20 cm. The outside diameter of each of the outer rings is 1 cm less than that of the ring above it. The bottom ring has an outside diameter of 3 cm. What is the distance, in cm, from the top of the top ring to the bottom of the bottom ring?
![]()
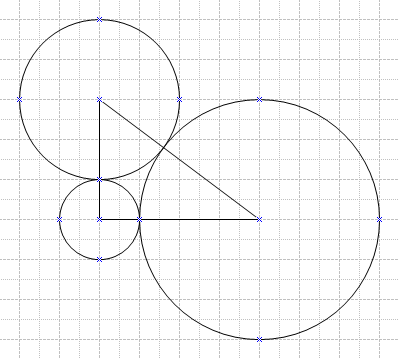
Problem 13
The vertices of a ![]() right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?
right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?
![]()
Problem 14
Two farmers agree that pigs are worth <dollar/>![]() and that goats are worth <dollar/>
and that goats are worth <dollar/>![]() . When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a <dollar/>
. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a <dollar/>![]() debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
![]()
![]()
![]()
![]()
![]()
![]()
Problem 15
Suppose ![]() and
and ![]() . What is the smallest possible positive value of
. What is the smallest possible positive value of ![]() ?
?
![]()
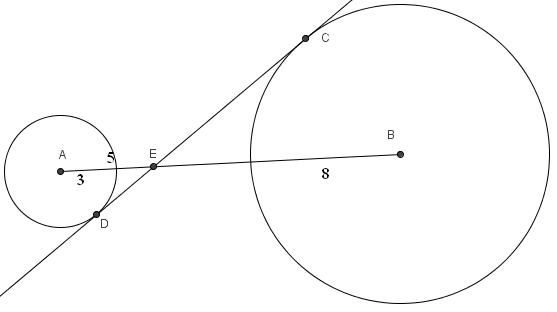
Problem 16
Circles with centers ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively. A common internal tangent intersects the circles at
, respectively. A common internal tangent intersects the circles at ![]() and
and ![]() , respectively. Lines
, respectively. Lines ![]() and
and ![]() intersect at
intersect at ![]() , and
, and ![]() . What is
. What is ![]() ?
?
![]()
Problem 17
Square ![]() has side length
has side length ![]() , a circle centered at
, a circle centered at ![]() has radius
has radius ![]() , and
, and ![]() and
and ![]() are both rational. The circle passes through
are both rational. The circle passes through ![]() , and
, and ![]() lies on
lies on ![]() . Point
. Point ![]() lies on the circle, on the same side of
lies on the circle, on the same side of ![]() as
as ![]() . Segment
. Segment ![]() is tangent to the circle, and
is tangent to the circle, and ![]() . What is
. What is ![]() ?
?
![]()
Problem 18
The function ![]() has the property that for each real number
has the property that for each real number ![]() in its domain,
in its domain, ![]() is also in its domain and
is also in its domain and
![]()
What is the largest set of real numbers that can be in the domain of ![]() ?
?
![]()
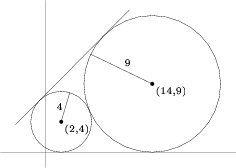
Problem 19
Circles with centers ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively. The equation of a common external tangent to the circles can be written in the form
, respectively. The equation of a common external tangent to the circles can be written in the form ![]() with
with ![]() . What is
. What is ![]() ?
?
![]()
Problem 20
A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once?
![]()
Problem 21
Let
![]()
and
![]() .
.
What is the ratio of the area of ![]() to the area of
to the area of ![]() ?
?
![]()
Problem 22
A circle of radius ![]() is concentric with and outside a regular hexagon of side length
is concentric with and outside a regular hexagon of side length ![]() . The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is
. The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is ![]() . What is
. What is ![]() ?
?
![]()
![]()
Problem 23
Given a finite sequence ![]() of
of ![]() real numbers, let
real numbers, let ![]() be the sequence
be the sequence
![]()
of ![]() real numbers. Define
real numbers. Define ![]() and, for each integer
and, for each integer ![]() ,
, ![]() , define
, define ![]() . Suppose
. Suppose ![]() , and let
, and let ![]() . If
. If ![]() , then what is
, then what is ![]() ?
?
![]()
Problem 24
The expression
![]()
is simplified by expanding it and combining like terms. How many terms are in the simplified expression?
![]()
Problem 25
How many non-empty subsets ![]() of
of ![]() have the following two properties?
have the following two properties?
![]() No two consecutive integers belong to
No two consecutive integers belong to ![]() .
.
![]() If
If ![]() contains
contains ![]() elements, then
elements, then ![]() contains no number less than
contains no number less than ![]() .
.
![]()